7. Интегрирование дробной рациональной функции
Рациональной
дробью
называется частное двух многочленов.
Если степень многочлена Р(х) больше или равна степени многочлена
Q(x), то дробь называется неправильной; в противном случае дробь называ-
ется правильной.
При интегрировании неправильной рациональной дроби нужно раз-
делить ее числитель Р(х) на знаменатель Q(x), тогда
, где S(x)
–частное, R(x)
– остаток деления и
.
Для интегрирования
правильной дроби
нужно записать ее в ви-
де суммы элементарных дробей исходя из разложения знаменателя Q(x) на
произведение линейных и квадратичных множителей следующим образом.
Пусть Q(x) имеет следующее разложение на множители:
,
где сумма
равна степени многочлена Q(x).
Тогда правильная
рациональная дробь
представима в виде следующей суммы
элементарных дробей:
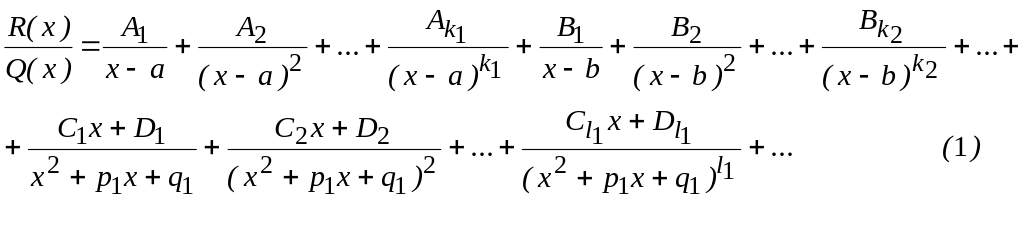
Для определения
коэффициентов
нужно привести к наименьшему общему знаменателю правую часть выра-
жения (1) и приравнять полученный в числителе дроби многочлен много-
члену R(x). Приравнивая коэффициенты при одинаковых степенях х этих
многочленов, получим систему линейных уравнений, которую нужно
решить.
Пример.
Вычислить интеграл
.
Решение. Под знаком интеграла имеем неправильную рациональную
дробь (числитель – многочлен пятой степени, знаменатель – второй).
Разделив
на
,
в частном получим
и в остатке
.
Тогда
.
Правильную
рациональную дробь
представим в виде сле-
дующей суммы элементарных дробей:
.
После приведения в последнем равенстве к общему знаменателю
получаем тождество
;
.
Имеем
, отсюда
,
.
Следовательно,
и
.
8. Интегрирование рациональных тригонометрических
функций.
Для
вычисления интегралов вида
,
где
−функция,
рациональная относительно sinx
и cosx,
следует использовать следующие
рекомендации.
1.
Для вычисления интегралов вида
,
где m
и n
– целые числа, при m
– положительном нечетном используется
подстановка
;
если n
– нечетное положительное – подстановка
.
Если показатели степеней m и n – четные, то следует понизить сте-
пень тригонометрических функций, используя соответствующие формулы
тригонометрии.
Если хотя бы один из четных показателей m или n отрицателен, то
применяют подстановки
или
.
Пример
1. Вычислить
интеграл
.
Решение. В нашем случае n = 3 – нечетное число, применяем подста-
новку
,
отсюда
.
Тогда
.
Пример
2. Вычислить
интеграл
.
Решение.
Применим подстановку
,
тогда
.
Имеем
2.
При вычислении интегралов вида
,
,
следует произведение тригонометрических
функций преобразовать в их сумму.
Пример
3. Вычислить
интеграл
.
Решение. Применим известную из тригонометрии формулу
.
Тогда
.
3. Часто к интегралу от рациональной функции приводит подстанов-
ка
.
В этом случае
,
,
.
Пример
4. Вычислить
интеграл
.
Решение. Делая подстановку , получаем
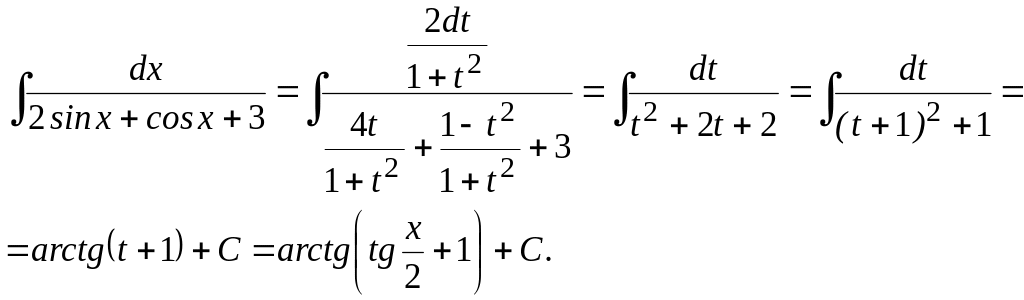
