1. 4. Линейные неоднородные дифференциальные уравнения

второго порядка с постоянными коэффициентами.

Общее решение у неоднородного уравнения равно сумме общего решения однородного уравнения и какого-нибудь частного решения неоднородного уравнения, то есть .

Для некоторых специальных видов функций частное решение

можно найти методом неопределенных коэффициентов в следующих

случаях.

Случай 1. Пусть , где - многочлен степени n.

Тогда , где - многочлен степени n, если число 0 не является корнем характеристического уравнения.

Если же 0 – корень кратности r характеристического уравнения, то .

Случай 2. , где a, m – действительные числа.

Тогда , если число m не является корнем характеристического

уравнения. Если же число m есть корень кратности r характеристическо-

го уравнения, то .

Здесь А – подлежащий определению коэффициент.

Случай 3. , где - многочлен степени n.

Тогда , если число m – не корень характеристического уравнения и , если число m является корнем кратности r характеристического уравнения.

Здесь - многочлен степени n, коэффициенты которого нужно определить.

Случай 4. .

В этом случае , если числа не являются корнями характеристического уравнения и , если числа есть корни характеристического уравнения.

Случай 5. , где р₁(х) и р₂(х) – многочлены.

Тогда , если числа не являются корнями характеристического уравнения и , если числа есть корни характеристического уравнения.

Здесь и - многочлены, степень которых равна большей из степеней многочленов р₁(х) и р₂(х).

Случай 6. .

Тогда , где и есть соответственно частные решения уравнений и .

Пример 1. Решить уравнение .

Решение. Находим общее решение однородного уравнения

. Его характеристическое уравнение имеет корни , .

Тогда .

Найдем частное решение данного неоднородного уравнения. Его

правая часть есть функция . Согласно случаю 1, так число 0 не

является корнем характеристического уравнения, есть многочлен второй степени, то есть . Отсюда находим ,

и, подставляя , , в данное уравнение, получаем тождество

или .

Приравнивая коэффициенты при одинаковых степенях х в обеих час-

тях последнего равенства (только при этом условии оно будет тождеством)

получаем систему уравнений

, из которой находим А = − 3, В = − 3, С = − 4,5.

Следовательно, и искомым общим решением данного неоднородного уравнения является .

Пример 2. Решить уравнение .

Решение. Характеристическое уравнение имеет корни

. Поэтому .

Частным решением данного неоднородного уравнения является функция ( в соответствии со случаем 3, так как не является корнем характеристического уравнения ).

Находим ,

.

Подставим , , в данное уравнение:

; ;

.

Приравняем коэффициенты при одинаковых степенях х в обеих час-

тях последнего тождества, получаем систему уравнений для определения

А и В :

, откуда , .

Следовательно, .

Значит, .

Пример 3. Найти частное решение уравнения , удовлетворяющее начальным условиям , .

Решение. Характеристическое уравнение имеет рав-

ные корни , поэтому .

Правая часть данного уравнения есть сумма показательной функции

и многочлена первой степени 2х – 4 (случай 6).

Так числа −2 и 0 не являются корнями характеристического уравнения, то .

Подставляя , , в данное уравнение, имеем:

.

Приравнивая коэффициенты подобных членов обеих частей этого

тождества, получаем систему уравнений

, откуда А = 1, В = 2, С = 0.

Следовательно, и общим решением данного уравнения

является функция .

Используя начальные условия, определим значения постоянных С₁

и С₂ . Так как , то С₁+1 = 1, С₁ = 0.

Находим производную .

Тогда С₁ + С₂ – 2 + 2 = 1, С₁ + С₂ = 1, С₂ = 1.

Итак, − искомое частное решение.

Выше были даны рекомендации по отысканию частного решения

неоднородного уравнения лишь для функций, приведенных в случаях 1 – 6.

Если же правая часть неоднородного уравнения есть функция другой

структуры, то для отыскания используется метод вариации произволь-

ных постоянных, состоящий в следующем.

Пусть общим решением однородного уравнения

является функция , где и − где

и − линейно независимые решения этого уравнения; С₁ и С₂ – постоянные величины.

Частное решение неоднородного уравнения ищется в виде , где функции и находятся решением следующей системы уравнений:

.

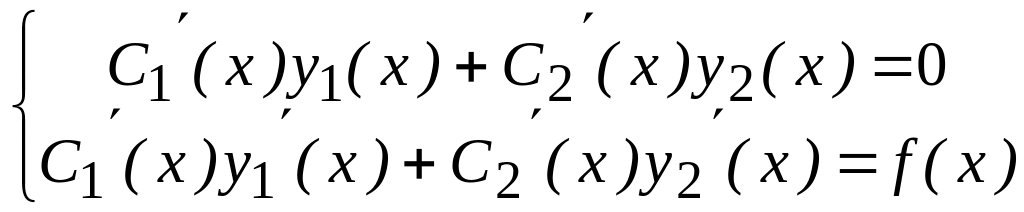Пример 4. Найти общее решение уравнения .

Решение. Характеристическое уравнение имеет корни

к_1,2 = ± i. Поэтому .

В нашем случае , − два линейно независимые частные решения однородного уравнения.

Для определения частного решения данного уравнения составим и решим следующую систему уравнений по формулам Крамера:

.

, ,

.

Имеем

, .

Отсюда

.

.

Так как (вычисляется подстановкой ), то .

Тогда

и

является общим решением данного уравнения.