Лекция 5.

Тема лекции: Дифференциальные уравнения высших порядков.

Оглавление:

1. Дифференциальные уравнения второго порядка.

1. 1. Дифференциальные уравнения второго порядка, допус-

кающие понижение порядка.

1. 2. Линейные дифференциальные уравнения второго

порядка.

1. 3. Линейные однородные дифференциальные уравнения

второго порядка с постоянными коэффициентами.

1. 4. Линейные неоднородные дифференциальные уравнения

второго порядка с постоянными коэффициентами.

2. Линейные дифференциальные уравнения высших порядков

с постоянными коэффициентами.

Цели лекции: научить решать отдельные типы дифференциальных уравнений второго и более высоких порядков.

После изучения рассматриваемого материала Вы сможете решать основные типы дифференциальных уравнений второго и более высоких порядков , использовать их в других разделах математики и специальных дисциплинах.

Информационные источники.

1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. М.: Высшая школа, 1996.

2. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: Наука, Любое издание.

3. Лычкин В.Н.Высшая математика. Учебное пособие. РГАЗУ, 2011.

4. Лычкин В.Н.Высшая математика в задачах. Учебное пособие. РГАЗУ, 2009.

5.Пискунов Н.С. Дифференциальное и интегральное исчисления.

Т. 1,2. М.; Наука (любое издание).

1. Дифференциальные уравнения второго порядка.

Дифференциальным уравнением второго порядка называется уравне-

ние вида (1) или (если его можно разрешить относительно ) вида . (2)

Общим решением дифференциального уравнения второго порядка

называется функция , обращающая уравнение в тождество

при любых значениях постоянных С₁ и С₂.

Решение уравнения второго порядка, получаемое из общего решения

при фиксированных значениях постоянных С₁ и С₂, называется частным

решением уравнения. Частное решение уравнения второго порядка находят

из общего его решения заданием начальных условий: , .

Задача отыскания частного решения дифференциального уравнения

второго порядка, удовлетворяющего заданным начальным условиям, назы-

вается задачей Коши.

1. 1. Дифференциальные уравнения второго порядка,

допускающие понижение порядка.

Рассмотрим следующие три вида дифференциальных уравнений вто-

рого порядка, сводящиеся к уравнениям первого порядка.

I. .

Запишем это уравнение в виде , .

Проинтегрировав дважды последнее уравнение, получим его общее решение:

, . (3)

Пример 1. Решить уравнение .

Решение. По формуле (3) получаем:

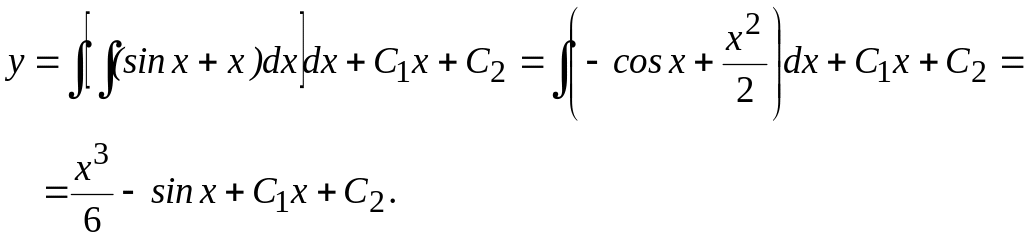
II. .

Для решения уравнений этого типа, не содержащих явным образом

функции у, применяют подстановку , где − функция аргумента х.

Тогда и рассматриваемое уравнение становится уравнением первого порядка относительно р.

Пример 2. Найти общее решение уравнения .

Решение. Правая часть уравнения не содержит явным образом функ-

цию у. Пусть , тогда .

Получаем

, , , , .

Так как , то и .

Для вычисления последнего интеграла применим формулу интегри-

рования по частям. Положим , , тогда , .

Имеем

− общее решение данного уравнения.

III. .

Здесь правая часть уравнения явно не содержит аргумента х. Приме-

ним подстановку , где р – функция от у.

Тогда

и данное уравнение сводится к уравнению первого порядка.

Пример 3. Найти частное решение уравнения , удовлетворяющее начальным условиям .

Решение. Данное уравнение явным образом не содержит аргумент х.

Пусть , где р- некоторая функция от у. Тогда и уравнение принимает вид , .

Интегрируя, получаем

, .

Так как , имеем , откуда С₁ = 1.

Тогда или , .

Разделив переменные в последнем уравнении, имеем .

Интегрируя, получим .

Используя начальное условие , находим .

Тогда , , − иско-

мое частное решение данного уравнения.