22. Угловая скорость и ускорение точек твердого тела при равнопеременном вращательном движении.

Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени .

Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости 

Вращательное движение с переменной угловой скоростью называется неравномерным. Если же угловое ускорение ε=const, то вращательное движение называется равнопеременным. Таким образом, равнопеременное вращение тела – частный случай неравномерного вращательного движения.

Равнопеременное вращение – угловое ускорение не изменяется по величине

У равнение равнопеременного вращения φ = φ₀ + ω₀t + εt²/2

У равнение угловой скорости ω = ω₀ + εt

у гловое ускорение не изменяется по величине

23.Сравнение формул кинематики для поступательного и вращательного движений.

Кинематические характеристики поступательного и вращательного движения. Связи между ними.

Основная задача кинематики состоит в определении положения и состояния объекта быстроту перемещения вектора средней скорости ; => . При вращательном движении точки лежащая на одном радиусе будут иметь разные линейные скорости, поэтому линейная скорость не может быть характеристикой вращательного движения, такой характеристикой является угол поворота.

T_вр = I_z²/2 – кинетическая энергия вращающегося тела; T=mv²/2 – поступательное движения (получено II З-н Ньютона + dA=dT *dr). При их сравнении следует, что момент инерции – мера инертности тела при вращательном движении. В случае плоского движения тел например цилиндра, скатывающегося по наклонной плоскости можно получить как сумма поступательного движения и энергии вращения.

Для характеристики быстроты изменения угла 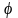вводят понятие угловой скорости. - угловая скорость. . - формула для расчета угла поворота

24. Основные законы динамики материальной точки. Инерциальная и неинерциальная системы отсчета. Дифференциальные уравнения движения материальной точки.

Динамика – раздел механики, в котором изучаются законы движения материальных тел под действием сил. Осн.законы механики (зак-ны Галилея-Нютона): закон инерции (1-ый закон): материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока действие других тел не изменит это состояние; основной закон динамики ( 2-ой закон (Ньютона)): ускорение матер.точки пропорционально приложенной к ней силе и имеет одинаковое с ней направление  ; закон равенства действия и противодействия (3-й закон (Ньютона)): всякому действию соответствует равное и противоположно направленное противодействие; закон независимости сил: несколько одновременно действующих на матер.точку сил сообщают точке такое ускорение, какое сообщила бы ей одна сила, равная их геометрической сумме.

Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой справедлив закон инерции: все свободные тела (то есть такие, на которые не действуют внешние силы или действие этих сил компенсируется) движутся прямолинейно и равномерно или покоятся^[1]. Эквивалентной является следующая формулировка, удобная для использования в теоретической механике^[2] : Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным, а время — однородным.

Неинерциа́льная систе́ма отсчёта — произвольная система отсчёта, не являющаяся инерциальной. Всякая система отсчета, движущаяся с ускорением относительно инерциальной является неинерциальной. При рассмотрении уравнений движения тела в неинерциальной системе отсчета необходимо учитывать дополнительные силы инерции. Законы Ньютона выполняются только в инерциальных системах отсчёта. Для того, чтобы найти уравнение движения в неинерциальной системе отсчёта, нужно знать законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной.

Дифференциальные уравнения движения материальной точки

Векторная форма (2-й закон Ньютона):

Координатная форма (2-й закон Ньютона в проекциях на оси декартовых координат):

Естественная (эйлерова) форма (2-й закон Ньютона в проекциях на оси естественных координат):

где х, у, z - координаты точки массой m; X, Y, Z - проекции действующей на точку силы (или равнодействующей действующих на точку сил)   на оси декартовых координат;  - проекции силы   на оси естественных координат: касательную Т, главную нормаль N и бинормаль В (см. рис. 1).

Рисунок 1.

Если точка является несвободной (на движение точки наложены связи), в число действующих на точку сил включаются реакции связей.

Силы, входящие в правую часть дифференциальных уравнений движения, в общем случае могут являться функциями от времени t, скорости v и координат х, у, z точки.

25. Две задачи динамики движущейся материальной точки. Движение тела, брошенного под углом к горизонту.

• Две основные задачи динамики:

1. Прямая задача: Задано движение (уравнения движения, траектория). Требуется определить силы, под действием которых происходит заданное движение.

2. Обратная задача: Заданы силы, под действием которых происходит движение. Требуется найти параметры движения (уравнения движения, траекторию движения).

Обе задачи решаются с помощью основного уравнения динамики и проекции его на координатные оси. Если рассматривается движение несвободной точки, то как и в статике, используется принцип освобождаемости от связей. В результате реакции связей включаются в состав сил, действующих на материальную точку. Решение первой задачи связано с операциями дифференцирования. Решение обратной задачи требует интегрирования соответствующих дифференциальных уравнений и это значительно сложнее, чем дифференцирование. Обратная задача сложнее прямой задачи.

Движение тела, брошенного с некоторой начальной скоростью V_о под углом α к горизонту, представляет собой сложное движение: равномерное по горизонтальному направлению и одновременно происходящее под действием силы тяжести равноускоренное движение в вертикальном направлении.

Координаты точки траектории описываются уравнениями:

X= u₀ *t*cos(α)

Y=u₀*t*sin(α)-gt²/2

Здесь: x, y — координаты тела, u₀ — начальная скорость тела (м/с), α — угол, под которым брошено тело к горизонту (°), g — ускорение свободного падения 9.81 (м/c2), t — время движения (c)

Уравнение движения тела, брошенного под углом к горизонту

общее уравнение движения тела, брошенного под углом к горизонту

X= x*tg() – g*x2/ 2*u₀²*cos(α)²

Так как ускорение свободного падения g, α — угол, под которым брошено тело к горизонту и начальная скорость тела u₀ —постоянные величины, то координата y пропорциональна квадрату x, т.е. траектория движения представляет собойпараболу, начальная точка находится на одной из ее ветвей, а вершина параболы, есть точка максимального подъема тела.