- •4. Формула мгновенной скорости.
- •6. Формула ускорения при криволинейном движении(по окружности)
- •7. Силы инерции
- •8. Силы инерции при криволинейном движении(по окруж)
- •Силовые поля
- •16. Определение консервативных сил
- •17. Доказать что работа консервативных сил на замкнутом пути равна 0
- •18. Физические поля(определение однородного поля)
- •19. Центральное поле силы(?!?)
- •22. Связь между потенциальной энергией и силой(формула с градиентом).
- •23. Полная механическая энергия
- •Полная механическая энергия: - характеризует движение и взаимодействие тел; и - является функцией скоростей и взаимного расположения тел.
- •24. Закон сохранения механической энергии для м.Т закон сохранения механической энергии
- •28. Момент инерции для тонкого однородного стержня(формула)
- •30. Кинетическая энергия вращения
- •31. Момент импульса.
- •32. Закон сохранения момента импульса. Закон сохранения момента импульса
- •33. Принцип относительности Галилея
- •34. Преобразование скоростей и ускорений .
- •35. Принцип относительности Эйнштейна
- •36.Принцип постоянства скорости света.
- •38.Следствия из преобразований Лоренца(время, длина)
- •39. Релятивистский закон сложения скоростей
- •42.Связь энергии с импульсом
- •43. Определение колебаний, их виды и характеристики
- •44. Математический,пружинный и физический маятники
- •45. Энергия гармонических колебаний
- •47. Вынужденные колебания
- •49. Упругие волны
- •51. Уравнение бегущей волны
- •52 Основные положения мкт: 3 основных положения молекулярно - кинетической теории:
- •1. Виды степеней свободы и число степеней свободы в идеальном газе
- •Формула
- •7.Явления переноса (диффузия, теплопроводность, вязкость)
- •8.Определение термодинамики и её параметров
- •9. Работа газов и изменение объемов
- •15. Работа при адиабатном процессе
- •16.Политропные процессы
- •18. Тепловая и холодильная машина
- •20. Цикл Карно и кпд идеального газа
- •21. Энтропия и её свойства
- •22 . Энтропия идеального газа
- •23 Статистический смысл 2-го начала термодинамики
- •24 Реальные газы
- •27. Экспериментальные изотермы реального газа
28. Момент инерции для тонкого однородного стержня(формула)
Стержень длины L и массы m |
|
|
Это выражение предполагает, что стержень имеет вид бесконечно тонкой, но жёсткой проволоки. Это частный случай предыдущего объекта для w = L и h = 0. (через центр) |
через
начало стержня -
![]()
29.
Теория Штейнера(определение М.И.
относительно любой оси)Теорема
Штейнера. Имеем тело, момент инерции
которого относительно оси, проходящей
через его центр масс
![]() известен.
Необходимо определить момент инерции
относительно произвольно оси
известен.
Необходимо определить момент инерции
относительно произвольно оси
![]() параллельной
оси
параллельной
оси
![]() .
Согласно теореме Штейнера, момент
инерции тела относительно произвольной
оси равен сумме момента инерции тела
относительно оси, проходящей через
центр масс и параллельной данной оси,
плюс произведение массы тела на квадрат
расстояния между осями:
.
Согласно теореме Штейнера, момент
инерции тела относительно произвольной
оси равен сумме момента инерции тела
относительно оси, проходящей через
центр масс и параллельной данной оси,
плюс произведение массы тела на квадрат
расстояния между осями:
|
30. Кинетическая энергия вращения
Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:
![]()
Если
тело вращается вокруг неподвижной оси
с угловой скоростью
,
то
линейная скорость i-ой точки равна
![]() ,
где
,
где
![]() ,
- расстояние от этой точки до оси вращения.
Следовательно.
,
- расстояние от этой точки до оси вращения.
Следовательно.
|
(5.11) |
где
![]() -
момент инерции тела относительно оси
вращения.
-
момент инерции тела относительно оси
вращения.
В
общем случае движение твердого тела
можно представить в виде суммы двух
движений - поступательного со скоростью,
равной скорости
![]() центра
инерции тела, и вращения с угловой
скоростью
вокруг
мгновенной оси, проходящей через центр
инерции. При этом выражение для
кинетической энергии тела преобразуется
к виду
центра
инерции тела, и вращения с угловой
скоростью
вокруг
мгновенной оси, проходящей через центр
инерции. При этом выражение для
кинетической энергии тела преобразуется
к виду
|
(5.12) |
где
![]() -
момент инерции тела относительно
мгновенной оси вращения, проходящей
через центр инерции.
-
момент инерции тела относительно
мгновенной оси вращения, проходящей
через центр инерции.
31. Момент импульса.
Векторное
произведение радиуса-вектора
![]() материальной
точки на ее импульс:
материальной
точки на ее импульс:
![]() называют
моментом импульса
называют
моментом импульса
![]() ,
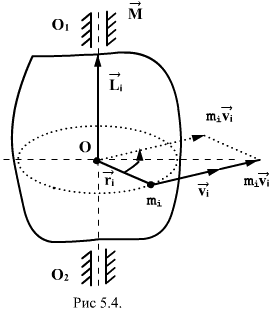
этой точки относительно точки О (рис.5.4)
,
этой точки относительно точки О (рис.5.4)
![]() .
Вектор
иногда
называют также моментом количества
движения материальной точки. Он направлен
вдоль оси вращения перпендикулярно
плоскости, проведенной через векторы
и
и
образует с ними правую тройку векторов
(при наблюдении из вершины вектора
видно, что вращение по кратчайшему
расстоянию от
к
происходит
против часовой стрелки).
.
Вектор
иногда
называют также моментом количества
движения материальной точки. Он направлен
вдоль оси вращения перпендикулярно
плоскости, проведенной через векторы
и
и
образует с ними правую тройку векторов
(при наблюдении из вершины вектора
видно, что вращение по кратчайшему
расстоянию от
к
происходит
против часовой стрелки).
Векторную
сумму моментов импульсов
всех
материальных точек системы называют
моментом импульса (количества движения)
![]() системы
относительно точки О:
системы
относительно точки О:
![]()
Векторы
и
взаимно
перпендикулярны и лежат в плоскости
перпендикулярной оси вращения тела.
Поэтому
![]() .
Сучетом связи линейных и угловых величин
.
Сучетом связи линейных и угловых величин
![]()
и
направлен вдоль оси вращения тела в ту
же сторону, что и вектор
![]() .
.
Таким образом.
![]()
Момент импульса тела относительно оси вращения
![]()
т.е.
|
(5.9) |
Следовательно, момент импульса тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость вращения тела вокруг этой оси.