44. Математический,пружинный и физический маятники

1. Пружинный маятник — это груз массой m, который подвешен на абсолютно упругой пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника имеет вид или Из формулы (1) вытекает, что пружинный маятник совершает гармонические колебания по закону х = Асоs(ω₀t+φ) с циклической частотой и периодом (3) Формула (3) верна для упругих колебаний в границах, в которых выполняется закон Гука, т. е. если масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, используя (2) и формулу потенциальной энергии предыдущего раздела, равна 2. Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела (рис. 1).

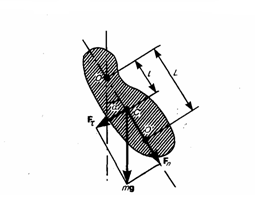
Рис.1

Если маятник из положения равновесия отклонили на некоторый угол α, то, используя уравнение динамики вращательного движения твердого тела, момент M возвращающей силы (4) где J — момент инерции маятника относительно оси, которая проходит через точку подвеса О, l – расстояние между осью и центром масс маятника, F_τ ≈ –mgsinα ≈ –mgα — возвращающая сила (знак минус указывает на то, что направления F_τ и α всегда противоположны; sinα ≈ α поскольку колебания маятника считаются малыми, т.е. маятника из положения равновесия отклоняется на малые углы). Уравнение (4) запишем как или Принимая (5) получим уравнение идентичное с (1), решение которого (1) найдем и запишем как: (6) Из формулы (6) вытекает, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω₀ и периодом (7) где введена величина L=J/(ml) — приведенная длина физического маятника. Точка О' на продолжении прямой ОС, которая отстоит от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качаний физического маятника (рис. 1). Применяя теорему Штейнера для момента инерции оси, найдем т. е. ОО' всегда больше ОС. Точка подвеса О маятника и центр качаний О' имеют свойство взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О подвеса будет новым центром качаний, и при этом не изменится период колебаний физического маятника. 3. Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити. Момент инерции математического маятника (8) где l — длина маятника. Поскольку математический маятник есть частный случай физического маятника, если предположить, что вся его масса сосредоточена в одной точке — центре масс, то, подставив (8) в (7), найдем выражение для периода малых колебаний математического маятника (9) Сопоставляя формулы (7) и (9), видим, что если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Значит, приведенная длина физического маятника — это длина такого математического маятника, у которого период колебаний совпадает с периодом колебаний данного физического маятника.