42.Связь энергии с импульсом

Релятивистский и классический импульс, m=1

Если частица с массой m движется со скоростью , то её энергия и импульс имеют следующую зависимость от скорости:

Эти соотношения обобщают классические выражения для энергии и импульса, получающиеся в результате разложения в ряд по :

При нулевой скорости, энергия частицы называется энергией покоя: . В современной физической литературе, принято, что m — масса частицы не зависит от скорости, являясь инвариантом относительно преобразований Лоренца, и является величиной неаддитивной. Понятие «релятивистской массы», зависящей от скорости не используется ^[25] , хотя оно и встречается в ранних работах по теории относительности. Историческая причина введения этого понятия была связана с попытками сохранить для релятивистского импульса классическую форму: .

При приближении скорости тела к скорости света, его энергия и импульс стремятся к бесконечности. Это одна из причин, по которой «обычные» объекты неспособны двигаться быстрее скорости света. Для частицы с ненулевой массой даже достижение скорости света потребует затраты бесконечной энергии. Заметные отклонения от классических выражений для энергии и импульса происходят при скоростях близких к скорости света. Если скорости относительно невелики, то отклонения от классической динамики незначительны. Например, при скорости u=c/4, относительная разница релятивистского и классического импульса составляет всего 3 %.

Между релятивистской энергией и импульсом существуют следующие связи:

Эти формулы остаются справедливыми и для объектов, движущихся со скоростью света. В этом случае их масса должна быть равна нулю m = 0.

• Колебания и волны.

43. Определение колебаний, их виды и характеристики

Периодическим колебанием называется процесс, при котором система (например, механическая) возвращается в одно и то же состояние через определенный промежуток времени. Этот промежуток времени называется периодом колебаний.

Возвращающая сила - сила, под действием которой происходит колебательный процесс. Эта сила стремится тело или материальную точку, отклоненную от положения покоя, вернуть в исходное положение.

В зависимости от характера воздействия на колеблющееся тело различают свободные (или собственные) колебания и вынужденные колебания.

Свободные колебания имеют место тогда, когда на колеблющееся тело действует только возвращающая сила. В том случае, если не происходит рассеивания энергии, свободные колебания являются незатухающими. Однако, реальные колебательные процессы являются затухающими, т.к. на колеблющееся тело действуют силы сопротивления движению (в основном силы трения).

Вынужденные колебания совершаются под действием внешней периодически изменяющейся силы, которую называют вынуждающей. Во многих случаях системы совершают колебания, которые можно считать гармоническими.

Гармоническими колебаниями называют такие колебательные движения, при которых смещение тела от положения равновесия совершается по закону синуса или косинуса:

(7.1)

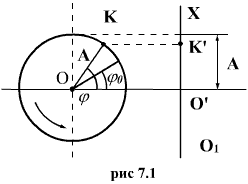
Для иллюстрации физического смысла рассмотрим окружность, и будем вращать радиус ОК с угловой скоростью ω против часовой (7.1) стрелки. Если в начальный момент времени ОК лежал в горизонтальной плоскости, то через время t он сместится на угол . Если начальный угол отличен от нуля и равен φ₀, тогда угол поворота будет равен Проекция на ось ХО₁ равна . По мере вращения радиуса ОК изменяется величина проекции, и точка будет совершать колебания относительно точки - вверх, вниз и т.д. При этом максимальное значение х равно А и называется амплитудой колебаний; ω - круговая или циклическая частота; - фаза колебаний; – начальная фаза. За один оборот точки К по окружности ее проекция совершит одно полное колебание и вернется в исходную точку.

Периодом Т называется время одного полного колебания. По истечению времени Т повторяются значения всех физических величин, характеризующих колебания. За один период колеблющаяся точка проходит путь, численно равный четырем амплитудам.

Угловая скорость определяется из условия, что за период Т радиус ОК сделает один оборот, т.е. повернется на угол 2π радиан:

или

Частота колебаний - число колебаний точки в одну секунду, т.е. частота колебаний определяется как величина, обратная периоду колебаний: