Выбор оптимального варианта использования производственного оборудования

Задача. На предприятии имеется три группы станков, каждая из которых может выполнять пять операций по обработке деталей (операции могут выполняться в любом порядке). Максимальное время работы каждой группы станков соответственно равно 100, 250, 180 ч. Каждая операция должна выполняться соответственно 100, 120, 70, 110, 130 ч.

Определить, сколько времени и на какую операцию нужно использовать каждую группу станков, чтобы обработать максимальное количество деталей.

Производительность каждой группы станков на каждую операцию задана матрицей

.

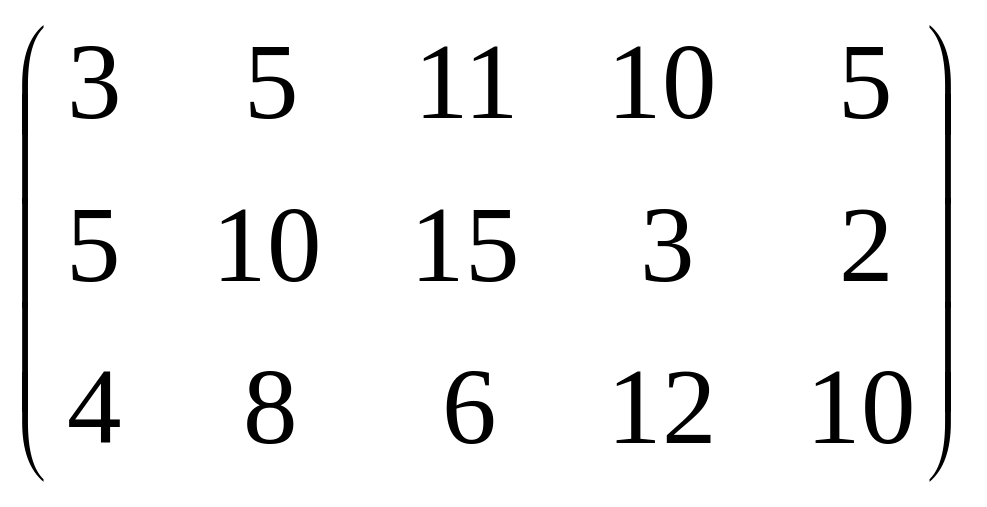РЕШЕНИЕ. Воспользуемся алгоритмом решения закрытой транспортной задачи.

Так как в задаче требуется найти максимум, а согласно алгоритму транспортной задачи находится минимум, тарифы умножим на (-1).

B j Ai	1	2	3	4	5	ui
	100	120	70	110	130
1 100	-3 40	-5	-11	-10	-5 60	0
2 250	-5 60	-10 120	-15 70	-3	-2	-2
3 180	-4	-8	-6	-12 110	-10 70	-5
vj	-3	-8	-13	-7	-5

Находим оценки свободных клеток: , , .

Так как > 0, перераспределим грузы, получим

60

130

Полученное перераспределение грузов занесём в табл.

B j Ai	1	2	3	4	5	ui
	100	120	70	110	130
1 100	-3 40	-5	-11	-10 60	-5	0
2 250	-5 60	-10 120	-15 70	-3	-2	-2
3 180	-4	-8	-6	-12 50	-10 130	-2
vj	-3	-8	-13	-10	-8

Оценки свободных клеток составляют

, , , , , , , .

Найденное решение является оптимальным, так как все оценки свободных клеток отрицательные. Итак,

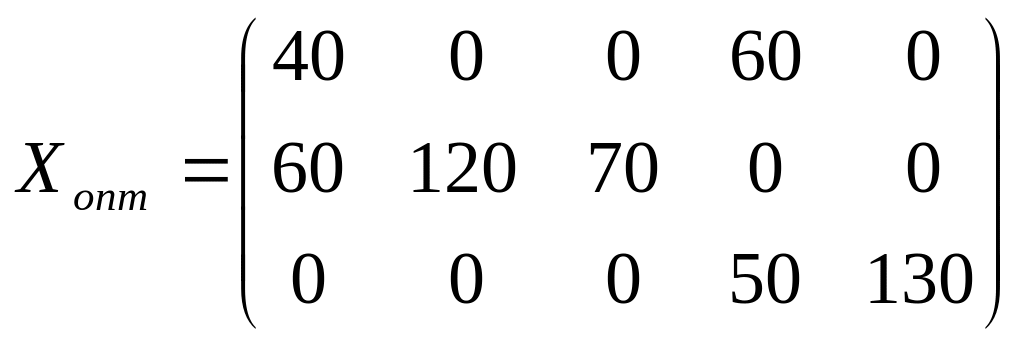
Таким образом, на первой группе станков целесообразно выполнять операции 1 и 4 продолжительностью 40 и 60 ч соответственно, на второй группе – операции 1, 2 и 3 продолжительностью 60, 120 и 70 ч соответственно, на третьей группе – операции 4 и 5 продолжительностью 50 и 130 ч соответственно. При этом максимальное число обработанных деталей составит 5170 шт.