Нахождение собственных векторов и собственных значений матриц
Собственными
векторами и собственными значениями
матрицы
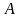называются вектора и числа, удовлетворяющие
соотношению:
,
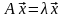причем собственный вектор определен с
точностью до постоянного множителя.
В
дальнейшем рассматриваются невырожденные
матрицы, имеющие различные собственные
значения Для нахождения собственных
значений необходимо решить уравнение:
.
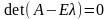Нахождение коэффициентов характеристического
полинома:
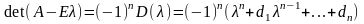
непосредственным
раскрытием определителя достаточно
громоздко. В методе Крылова используется
то, что подстановка в характеристический
полином вместо переменной матрицы
дает в результате нулевую матрицу:
.
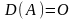Это тождество помножается слева на
произвольный вектор
:
,
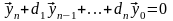где
,
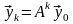то есть получается СЛАУ относительно
коэффициентов характеристического
полинома
.
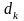Для определения собственных векторов
вводится система полиномов
,
,
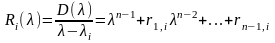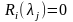если
.
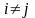Учитывается,
что собственные вектора
линейно независимые, то есть любой
вектор можно представить в виде их
линейной комбинации:
.
Собственный
вектор является линейной комбинацией
векторов
и коэффициентов полинома
.
Действительно:
Коэффициенты
при собственных векторах представляют
собой
,
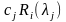которые все равны нулю кроме коэффициента
с
,
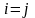стоящего перед
.
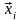То есть данная линейная комбинация
является собственным вектором.
1 Существует ряд методов аналогичных методу Гаусса (например, метод оптимального исключения [4] стр.31).
2 Студентам можно предложить самостоятельно построить свой метод исключения неизвестных.