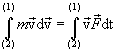- •8. Силы инерции при криволинейном движении(по окруж)
- •Силовые поля
- •Полная механическая энергия: - характеризует движение и взаимодействие тел; и - является функцией скоростей и взаимного расположения тел.
- •Закон сохранения механической энергии
- •30. Кинетическая энергия вращения
- •32. Закон сохранения момента импульса. Закон сохранения момента импульса
- •33. Принцип относительности Галилея
- •34. Преобразование скоростей и ускорений .
- •35. Принцип относительности Эйнштейна
Силовые поля
Этим полям соответствуют кулоновские силы (силы электростатического взаимодействия) и силы гравитационные (силы Всемирного тяготения. Сходство между ними заключается в том, что они могут быть обнаружены во время взаимодействия материальных объектов, причем в случае гравитации свойством, обуславливающим это взаимодействие, является масса, а в случае кулоновского взаимодействия — заряд, этой массой переносимый. Заряды, не связанные с массой, классической физике неизвестны.
При сохранении подобия в геометрических размерах тел и их взаимного расстояния, силы взаимного тяготения, равно как и силы электростатические (кулоновские) растут пропорционально 4-й степени абсолютных размеров рассматриваемой модели. В то же самое время в случае электрического взаимодействия, где между величиной заряда и размерами тел, несущих эти заряды, нет определённой связи, силы взаимодействия ослабляются пропорционально 2-й степени абсолютных размеров . Поэтому при сравнении этих сил в микромире доминируют Кулоновские силы, а в масштабах Вселенной — силы Всемирного тяготения.
12. Работа на участке + следствия(значение угла)
работой, совершаемой силой при прохождении телом пути , называют величину
|
(4.1) |
где а - угол между силой и направлением движения тела.
Работа - скалярная величина. Если вектор силы и вектор перемещений образуют острый угол т.е. , то , если , то , т.е. сила, действующая перпендикулярно к перемещению тела, работы не совершает.
В общем случае тело может двигаться произвольным, достаточно сложным образом (рис.4.2). Выделим элементарный участок пути , на котором силу можно считать постоянной и перемещение прямолинейным. Элементарная работа на этом участке равна
|
(4.2) |
Полная работа на пути определяется интегралом
|
|
13.Определение мощности + формула(обычная + мгновенная)
Мо́щность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
|
||
|
Так как работа является мерой изменения энергии, мощность можно определить также как скорость изменения энергии системы.Единица мощности[N] = 1 Вт = 1 Дж/с.
Кинетическая и потенциальная энергия.
14. Определение кинетической энергии + формула + следствия.Рассмотрим случай, когда материальная точка движется из точки 1 в точку 2 под действием приложенных к ней сил (рис.4.4.)

Причем силы, действующие на материальную точку, могут иметь разную природу, т.е. могут быть консервативными и неконсервативными. Уравнение движения в этом случае запишется в виде
|
(4.6) |
где
![]() Перепишем
(4.6) в виде
Перепишем
(4.6) в виде
|
(4.7) |
Умножим скалярно уравнение (4.7) на и проинтегрируем от точки1 до точки 2, получим:
|
(4.8) |
Учитываем
то, что
![]() ,
и интеграл в правой части выражения
(4.8) представляет собой работу всех сил,
на участке 1-2, можно записать:
,
и интеграл в правой части выражения
(4.8) представляет собой работу всех сил,
на участке 1-2, можно записать:
|
(4.9) |
величина
|
(4.10) |
называется кинетической энергией материальной точки. Таким образом, кинетическая энергия материальной точки – это энергия, которой обладает эта точка вследствие своего движения.
Из полученного выражения (4.9) следует, что работа всех сил, действующих на материальную точку на участке траектории 1-2 равна изменению ее кинетической энергии на этом участке.
15. Определение потенциальной энергии + формула + условие
Потенциальная
энергия - это энергия, обусловленная
взаимным расположением тел и характером
их взаимодействия. При соответствующих
условиях возможно изменение потенциальной
энергии, за счет чего совершается работа.
Для поднятия тела массой m на высоту
![]() необходимо
совершить работу против сил тяготения
Р:
необходимо
совершить работу против сил тяготения
Р:
![]() ,
,
знак минус перед интегралом, т.к. сила Р направлена в сторону противоположную изменению h.
Проинтегрируем это выражение:
![]()
Эта энергия пойдет на увеличение энергии замкнутой системы тело-Земля т.е. численно равна
![]()
Считая
поверхности Земли
![]() ,
получим
,
получим
![]()
Эта
энергия
![]() системы
тело - Земля и является потенциальной
энергиейтела, поднятого на высоту h:
системы
тело - Земля и является потенциальной
энергиейтела, поднятого на высоту h:
|
16. Определение консервативных сил

Силу
,
действующую на материальную точку,
называют консервативной или
потенциальной, если работа
![]() ,
совершаемая этой силой при перемещении
этой точки из произвольного положения
1 в другое 2, не зависит от того, по какой
траектории это перемещение произошло:
,
совершаемая этой силой при перемещении
этой точки из произвольного положения
1 в другое 2, не зависит от того, по какой
траектории это перемещение произошло:
![]()
Примером консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия заряженных тел. Поле, работа сил которого по перемещению материальной точки вдоль произвольной замкнутой траектории равна нулю, называется потенциальным.
17. Доказать что работа консервативных сил на замкнутом пути равна 0
Силу , действующую на материальную точку, называют консервативной или потенциальной, если работа , совершаемая этой силой при перемещении этой точки из произвольного положения 1 в другое 2, не зависит от того, по какой траектории это перемещение произошло:
Изменение
направления движения точки вдоль
траектории на противоположное вызывает
изменение знака консервативной силы,
так как величина
![]() меняет
знак. Поэтому при перемещении материальной
точки вдоль замкнутой траектории
меняет
знак. Поэтому при перемещении материальной
точки вдоль замкнутой траектории
![]() ,
например
,
например
![]() ,
работа консервативной силы равна нулю.
,
работа консервативной силы равна нулю.
![]()
18. Физические поля(определение однородного поля)
Поля физические, особая форма материи; физическая система, обладающая бесконечно большим числом степеней свободы. Примерами Поля физические могут служить электромагнитное и гравитационное поля, поле ядерных сил, а также волновые (квантованные) поля, соответствующие различным частицам. Впервые (30-е гг. 19 в.) понятие поля (электрического и магнитного) было введено М. Фарадеем. Концепция поля была принята им как альтернатива теории дальнодействия, т. е. взаимодействия частиц на расстоянии без какого-либо промежуточного агента (так интерпретировалось, например, электростатическое взаимодействие заряженных частиц по закону Кулона или гравитационное взаимодействие тел по закону всемирного тяготения Ньютона). Концепция поля явилась возрождением теории близкодействия, основоположником которой был Р. Декарт (1-я половина 17 в.). В 60-х гг. 19 в. Дж. К. Максвелл развил идею Фарадея об электромагнитном поле и сформулировал математически его законы (см. Максвелла уравнения). Согласно концепции поля, частицы, участвующие в каком-либо взаимодействии (например, электромагнитном или гравитационном), создают в каждой точке окружающего их пространства особое состояние — поле сил, проявляющееся в силовом воздействии на др. частицы, помещаемые в какую-либо точку этого пространства. Первоначально выдвигалась механистическая интерпретация поля как упругих напряжений гипотетической среды — «эфира». Однако наделение «эфира» свойствами упругой среды оказалось в резком противоречии с результатами проведённых позднее опытов. С точки зрения современных представлений, такая механистическая интерпретация поля вообще бессмысленна, поскольку сами упругие свойства макроскопических тел полностью объясняются электромагнитными взаимодействиями частиц, из которых состоят эти тела. Теория относительности, отвергнув концепцию «эфира» как особой упругой среды, вместе с тем придала фундаментальный смысл понятию Поля физические как первичной физической реальности. Действительно, согласно теории относительности, скорость распространения любого взаимодействия не может превышать скорости света в вакууме. Поэтому в системе взаимодействующих частиц сила, действующая в данный момент времени на какую-либо частицу системы, не определяется расположением др. частиц в этот же момент времени, т. е. изменение положения одной частицы сказывается на др. частице не сразу, а через определённый промежуток времени. Т. о., взаимодействие частиц, относительная скорость которых сравнима со скоростью света, можно описывать только через создаваемые ими поля. Изменение состояния (или положения) одной из частиц приводит к изменению создаваемого ею поля, которое отражается на др. частице лишь через конечный промежуток времени, необходимый для распространения этого изменения до частицы. Поля физические не только осуществляют взаимодействие между частицами; могут существовать и проявляться свободные Поля физические независимо от создавших их частиц (например, электромагнитные волны). Поэтому ясно, что Поля физические следует рассматривать как особую форму материи.
Однородное поле — это электрическое поле, в котором напряжённость одинакова по модулю и направлению во всех точках пространства. Приблизительно однородным является поле между двумя разноимённо заряженными плоскими металлическими пластинами. В однородном электрическом поле линии напряжённости направлены параллельно друг другу. Поле тяготения называется однородным, если его напряженность во всех точках одинакова
19. Центральное поле силы(?!?)
Закон
тяготения Ньютона определяет зависимость
силы тяготения от масс взаимодействующих
тел и расстояния между ними, но при это
он не показывает, каким образом
осуществляется это взаимодействие.
Тяготение относится к особой группе
взаимодействий. Силы тяготения, например,
не зависят от того, в какой среде
взаимодействующие тела находятся.
Тяготение существует и в вакууме.
Гравитационное взаимодействие
между телами осуществляется с помощью
поля
тяготения,
или гравитационного
поля.
Это поле порождается телами и является
формой существования материи. Основное
свойство поля тяготения заключается в
том, что на всякое тело массой m, внесенное
в это поле, действует сила тяготения,
т. е.
![]() (1)
Вектор g
не зависит от m и называется напряженностью
поля тяготения. Напряженность поля
тяготения определяется силой, которая
действует со стороны поля на материальную
точку единичной массы, и совпадает по
направлению с действующей силой.
Напряженность есть силовая характеристика
поля тяготения.
Поле тяготения
называется однородным,
если его напряженность во всех точках
одинакова, и центральным,
если во всех точках поля векторы
напряженности направлены вдоль прямых,
которые пересекаются в одной точке (А),
которая неподвижна по отношению к
какой-либо инерциальной системе отсчета
(рис. 1).
(1)
Вектор g
не зависит от m и называется напряженностью
поля тяготения. Напряженность поля
тяготения определяется силой, которая
действует со стороны поля на материальную
точку единичной массы, и совпадает по
направлению с действующей силой.
Напряженность есть силовая характеристика
поля тяготения.
Поле тяготения
называется однородным,
если его напряженность во всех точках
одинакова, и центральным,
если во всех точках поля векторы
напряженности направлены вдоль прямых,
которые пересекаются в одной точке (А),
которая неподвижна по отношению к
какой-либо инерциальной системе отсчета
(рис. 1).
Рис.1 Для графического изображения силового поля используются силовые линии (линии напряженности), которые рисуются таким образом, что вектор напряженности поля направлен по касательной к силовой линии.
20.
Работа поля тяготения. Потенциальная
энергия в поле гравитационного
взаимодействия(формулы).Определим
работу, которую совершают силы поля
тяготения при перемещении в поле
материальной точки массой m. Вычислим,
какую надо затратить работу для удаления
тела массой m от Земли. На расстоянии R
(рис. 1) на тело действует сила
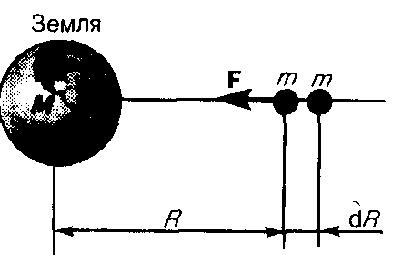
![]() При
перемещении этого тела на расстояние
dR совершается работа
При
перемещении этого тела на расстояние
dR совершается работа
![]() Знак
минус появляется потому, что сила и
перемещение в данном случае противоположны
по направлению
Если тело перемещать
с расстояния R1
до R2,
то работа
Знак
минус появляется потому, что сила и
перемещение в данном случае противоположны
по направлению
Если тело перемещать
с расстояния R1
до R2,
то работа
![]() (2)
Из формулы (2) следует, что затраченная
работа в поле тяготения не зависит от
траектории перемещения, а зависит лишь
от начального и конечного положения
тела, т. е. силы
тяготения
действительно консервативны,
а поле тяготения является потенциальным.
Работа, совершаемая консервативными
силами, равна изменению потенциальной
энергии системы, взятому со знаком
минус, т. е.
(2)
Из формулы (2) следует, что затраченная
работа в поле тяготения не зависит от
траектории перемещения, а зависит лишь
от начального и конечного положения
тела, т. е. силы
тяготения
действительно консервативны,
а поле тяготения является потенциальным.
Работа, совершаемая консервативными
силами, равна изменению потенциальной
энергии системы, взятому со знаком
минус, т. е.
![]() Из
формулы (2) получаем
Из
формулы (2) получаем
![]() (3)
Так как в формулы входит только разность
потенциальных энергий в двух состояниях,
то для удобства принимают потенциальную
энергию при R2→∞
равной нулю (P2=0).
Тогда (3) запишется в виде P1=
-GmM/R1.
Поскольку первую точку мы выбрали
произвольно, то
(3)
Так как в формулы входит только разность
потенциальных энергий в двух состояниях,
то для удобства принимают потенциальную
энергию при R2→∞
равной нулю (P2=0).
Тогда (3) запишется в виде P1=
-GmM/R1.
Поскольку первую точку мы выбрали
произвольно, то
![]() Величина
Величина
![]() является
энергетической характеристикой поля
тяготения и называется потенциалом.
Потенциал
поля тяготения
φ - скалярная величина, которая определяется
потенциальной энергией тела единичной
массы в данной точке поля или работой
по перемещению единичной массы из данной
точки поля в бесконечность. Таким
образом, потенциал поля тяготения,
создаваемого телом массой М, равен
является
энергетической характеристикой поля
тяготения и называется потенциалом.
Потенциал
поля тяготения
φ - скалярная величина, которая определяется
потенциальной энергией тела единичной
массы в данной точке поля или работой
по перемещению единичной массы из данной
точки поля в бесконечность. Таким
образом, потенциал поля тяготения,
создаваемого телом массой М, равен
![]() (4)
где R - расстояние от этого тела до
рассматриваемой точки.
Из формулы
(4) следует, что геометрическое место
точек с равными потенциалами образует
сферическую поверхность (R=const). Такие
поверхности, для которых потенциал
постоянен, называются эквипотенциальными.
Исследуем взаимосвязь между
потенциалом φ поля тяготения и его
напряженностью g. Из выражений (1) и (4)
вытекает, что элементарная работа dA,
совершаемая силами поля при малом
перемещении тела массой m, равна
(4)
где R - расстояние от этого тела до
рассматриваемой точки.
Из формулы
(4) следует, что геометрическое место
точек с равными потенциалами образует
сферическую поверхность (R=const). Такие
поверхности, для которых потенциал
постоянен, называются эквипотенциальными.
Исследуем взаимосвязь между
потенциалом φ поля тяготения и его
напряженностью g. Из выражений (1) и (4)
вытекает, что элементарная работа dA,
совершаемая силами поля при малом
перемещении тела массой m, равна
![]() С
другой стороны, dA=Fdl
(dl
- элементарное перемещение). Учитывая
(24.1), полу¬чаем, что dA=mgdl,
т. е. mgdl=
-mdφ, или
С
другой стороны, dA=Fdl
(dl
- элементарное перемещение). Учитывая
(24.1), полу¬чаем, что dA=mgdl,
т. е. mgdl=
-mdφ, или
![]() Величина
dφ/dl
характеризует изменение потенциала на
единицу длины в направлении перемещения
в поле тяготения. Можно показать, что
Величина
dφ/dl
характеризует изменение потенциала на
единицу длины в направлении перемещения
в поле тяготения. Можно показать, что
![]() (5)
где
(5)
где
![]() -
градиент скаляра φ. Знак минус в формуле
(5) показывает, что вектор напряженности
g
направлен в сторону убывания потенциала.
В качестве частного примера, исходя
из представлений теории тяготения,
рассмотрим потенциальную энергию тела,
находящегося на высоте h относительно
Земли:
-
градиент скаляра φ. Знак минус в формуле
(5) показывает, что вектор напряженности
g
направлен в сторону убывания потенциала.
В качестве частного примера, исходя
из представлений теории тяготения,
рассмотрим потенциальную энергию тела,
находящегося на высоте h относительно
Земли:
![]() где
R0
- радиус Земли. Так как
где
R0
- радиус Земли. Так как
![]() и
и
![]() то,
учитывая условие h<<R0,
получаем
то,
учитывая условие h<<R0,
получаем
![]()
21. Потенциальная энергия в поле силы упругости.
Потенциальная
энергия определяет силы упругости и
силы тяжести, ее используют для определения
электрических и магнитных сил, сил
ядерного взаимодействия.
Однако, как
это ни удивительно, никакого четкого
определения этому понятию не дается.
Просто утверждается, что она является
частью общей механической энергии
системы, зависящей от взаимного
расположения материальных точек,
составляющих эту систему, и от их
положений во внешнем силовом поле.
Численно же потенциальная энергия
системы в данном ее положении равна
работе, которую произведут действующие
на систему силы при перемещении этой
системы из этого положения в то, где
потенциальная энергия условно принимается
равной нулю.
Из этого определения
следует, что потенциальная энергия
характеризуется работой, которую она
может совершить при определенных
перемещениях материальной системы или
отдельного материального объекта. И
так как работа определяется через силу,
то, по сути дела, потенциальная энергия
является некоторым свойством действующих
на систему сил. Если же иметь в виду, что
само понятие силы тоже не имеет четкого
физического определения, то вполне
очевидно, что и определение потенциальной
энергии страдает таким же недостатком.
Из
определения потенциальной энергии
также следует, что это понятие имеет
место только для консервативных систем,
у которых работа действующих сил зависит
только от начального и конечного
положения системы. Так, для груза весом
G,
поднятого на высоту h,
потенциальная энергия будет равна:
![]() ;
(1)
для груза, прикрепленного к
пружине:
;
(1)
для груза, прикрепленного к
пружине:
![]() ,
(2)
где
,
(2)
где
![]() -
удлинение или сжатие пружины, k
– ее коэффициент жесткости; для двух
частиц с массами
-
удлинение или сжатие пружины, k
– ее коэффициент жесткости; для двух
частиц с массами
![]() и
и
![]() ,
притягивающихся по закону всемирного
тяготения:
,
притягивающихся по закону всемирного
тяготения:
![]() ,
(3)
где f
– гравитационная постоянная, r
– расстояние между частицами; аналогично
потенциальная энергия определяется и
для двух точечных электрических зарядов
,
(3)
где f
– гравитационная постоянная, r
– расстояние между частицами; аналогично
потенциальная энергия определяется и
для двух точечных электрических зарядов
![]() и
и
![]() .
Несмотря
на то, что потенциальная энергия
определяется через работу сил, она, в
свою очередь, используется для определения
этих сил, для чего используются частные
производные:
.
Несмотря
на то, что потенциальная энергия
определяется через работу сил, она, в
свою очередь, используется для определения
этих сил, для чего используются частные
производные:
![]() ,
(4)
которые эквивалентны одному
векторному выражению:
,
(4)
которые эквивалентны одному
векторному выражению:
![]() ,
(5)
в котором правая часть является
градиентом потенциальной энергии.
Очевидно,
для использования приведенных выражений
необходимо, чтобы потенциальная энергия
П
была нам известна и была бы однозначной
функцией координат X,
Y,
Z.
Выше
нами было показано, что силы инерции
представляют собой упругие силы,
обусловленные деформацией тел. Упругие
же силы, в свою очередь, могут быть
выражены только через потенциальную
энергию деформации. Поэтому для нас
очень важно выяснить физическую сущность
потенциальной энергии. Для этого нам
придется опуститься на более низкий
уровень структурной организации материи,
а именно на микроуровень, и посмотреть,
что же происходит с атомами при деформации
тел (рис.1).
Вполне очевидно, что при
деформации тел будут происходить
деформации орбит электронов. Здесь
может быть несколько видов деформаций:
деформации всестороннего растяжения
или сжатия (рис.1,а,б) и деформации
одностороннего растяжения или сжатия
(рис.1,в,г).
При всестороннем растяжении
или сжатии форма начальной равновесной
круговой орбиты не изменится, только
электроны переместятся на более высокий
или более низкий уровень. Однако,
соотношение между центробежными и
центростремительными силами электрического
притяжения изменится, они уже не будут
уравновешивать друг друга.
В равновесном
состоянии центробежная сила инерции,
действующая на электрон, будет равна:
,
(5)
в котором правая часть является
градиентом потенциальной энергии.
Очевидно,
для использования приведенных выражений
необходимо, чтобы потенциальная энергия
П
была нам известна и была бы однозначной
функцией координат X,
Y,
Z.
Выше
нами было показано, что силы инерции
представляют собой упругие силы,
обусловленные деформацией тел. Упругие
же силы, в свою очередь, могут быть
выражены только через потенциальную
энергию деформации. Поэтому для нас
очень важно выяснить физическую сущность
потенциальной энергии. Для этого нам
придется опуститься на более низкий
уровень структурной организации материи,
а именно на микроуровень, и посмотреть,
что же происходит с атомами при деформации
тел (рис.1).
Вполне очевидно, что при
деформации тел будут происходить
деформации орбит электронов. Здесь
может быть несколько видов деформаций:
деформации всестороннего растяжения
или сжатия (рис.1,а,б) и деформации
одностороннего растяжения или сжатия
(рис.1,в,г).
При всестороннем растяжении
или сжатии форма начальной равновесной
круговой орбиты не изменится, только
электроны переместятся на более высокий
или более низкий уровень. Однако,
соотношение между центробежными и
центростремительными силами электрического
притяжения изменится, они уже не будут
уравновешивать друг друга.
В равновесном
состоянии центробежная сила инерции,
действующая на электрон, будет равна:
![]() ,
(6)
где
,
(6)
где
![]() -
масса электрона,
-
масса электрона,
![]() -
окружная скорость электрона, соответствующая
радиусу
-
окружная скорость электрона, соответствующая
радиусу
![]() .
После
деформации величина центробежной силы
определится выражением:
.
После
деформации величина центробежной силы
определится выражением:
![]() ,
(7)
где
,
(7)
где
![]() -
окружная скорость электрона, соответствующая
радиусу r.
Поскольку
при переходе электрона с одной орбиты
на другую орбиту должен выполняться
закон сохранения момента количества
движения:
-
окружная скорость электрона, соответствующая
радиусу r.
Поскольку
при переходе электрона с одной орбиты
на другую орбиту должен выполняться
закон сохранения момента количества
движения:
![]() ,
(8)
преобразуем выражение (7), подставив
в него значение скорости
,
найденное из выражения (8):
,
(8)
преобразуем выражение (7), подставив
в него значение скорости
,
найденное из выражения (8):
![]() (9)
В
результате получим:
(9)
В
результате получим:
![]() (10)
После
этого можно найти отношение центробежных
сил
(10)
После
этого можно найти отношение центробежных
сил
![]() и
и
![]() :
:
![]() (11)
Силы
электрического притяжения между ядром
и электроном будут изменяться в
соответствии с законом Кулона:
(11)
Силы
электрического притяжения между ядром
и электроном будут изменяться в
соответствии с законом Кулона:
![]() ,
(12)
,
(12)
![]() ,
(13)
где k
–
коэффициент пропорциональности,
зависящий от выбора единиц измерения.
В системе СИ
,
(13)
где k
–
коэффициент пропорциональности,
зависящий от выбора единиц измерения.
В системе СИ
![]() ,
,
![]() -
электрическая постоянная (или
диэлектрическая проницаемость вакуума),
равная
-
электрическая постоянная (или
диэлектрическая проницаемость вакуума),
равная
![]() .
Отношение
сил электрического притяжения будет
равно:
.
Отношение
сил электрического притяжения будет
равно:
![]() (14)
Имея
в виду равенство
(14)
Имея
в виду равенство
![]() ,
найдем отношение центробежной силы
инерции и силы электрического
притяжения:
,
найдем отношение центробежной силы
инерции и силы электрического
притяжения:
![]() ,
(15)
откуда получим:
,
(15)
откуда получим:
![]() (16)
Разность
между центробежной и электрической
силами в зависимости от величины
деформации определится выражением:
(16)
Разность
между центробежной и электрической
силами в зависимости от величины
деформации определится выражением:
![]() ,
(17)
где
,
(17)
где
![]() .
При
.
При
![]() (растяжение)
(растяжение)
![]() и
и
![]() ,
то есть сила, противодействующая
растяжению, будет направлена к центру
атома.
При
,
то есть сила, противодействующая
растяжению, будет направлена к центру
атома.
При
![]() (сжатие)
(сжатие)
![]() и
и
![]() ,
то есть противодействующая сила
направлена во внешнюю сторону.
В
случае одностороннего растяжения
(рис.1,в) и сжатия (рис.1,г) орбиты электронов
будут деформироваться в эллиптические
кривые, что также приведет к появлению
противодействующих сил
,
то есть противодействующая сила
направлена во внешнюю сторону.
В
случае одностороннего растяжения
(рис.1,в) и сжатия (рис.1,г) орбиты электронов
будут деформироваться в эллиптические
кривые, что также приведет к появлению
противодействующих сил
![]() ,
обусловленных наличием сил инерции.
Параметры
орбиты электронов могут быть найдены
по формулам, полученным в главе III §10
для движения планет.
Таким образом,
мы показали, что упругие силы, появляющиеся
при деформации тел, являются результатом
действия сил инерции на электроны в
атомах тел. Ниже также будет показано,
что и силы электрического притяжения
будут иметь инерционную природу.
Напомним, что силы инерции, в свою
очередь, являются следствием ускоренного
движения материальных объектов при
наличии неоднородного поля кинетической
энергии. Такое поле и существует во
вращающихся вокруг ядра электронах.
Значит, и электроны должны деформироваться
при своем вращении вокруг ядра атома и
при вращении вокруг своей оси.
Интересно
отметить, что при прямолинейном движении
тел с постоянным ускорением градиента
скорости по их длине в направлении
движения не будет, хотя на них и будут
действовать силы инерции. Такое положение
как раз и объясняется тем, что действие
сил инерции перемещается на микрочастицы,
из которых состоит тело. Результирующая
же сила инерции, действующая на тело в
целом, будет представлять собой сумму
микроинерционных сил, действующих на
каждый электрон.
Потенциальная
энергия также будет являться следствием
действия микроинерционных сил,
обусловленных движением микрочастиц
в пространстве, поэтому можно утверждать,
что потенциальная энергия является
свойством кинетической энергии тела,
но не на макро, а на микроуровне его
структурной организации, которая,
однако, зависит от скорости изменения
кинетической энергии при движении всего
тела в целом, то есть от действующей на
него внешней силы. В этом и будет
заключаться физическая сущность
потенциальной энергии.
На первый
взгляд может показаться, что такое
определение потенциальной энергии
будет справедливо только при упругих
деформациях тел, но не может характеризовать
физической сущности потенциальной
энергии, например, поля тяготения.
Однако, это не так. Ниже нами будет
показано, что силы тяготения могут быть
объяснены упругими деформациями частиц
вакуума, с движением которых связано
существование поля кинетической энергии,
через посредство которого и могут быть
найдены эти силы. То же самое можно
сказать и о других видах потенциальной
энергии, возникающей при взаимодействии
материальных объектов.
,
обусловленных наличием сил инерции.
Параметры
орбиты электронов могут быть найдены
по формулам, полученным в главе III §10
для движения планет.
Таким образом,
мы показали, что упругие силы, появляющиеся
при деформации тел, являются результатом
действия сил инерции на электроны в
атомах тел. Ниже также будет показано,
что и силы электрического притяжения
будут иметь инерционную природу.
Напомним, что силы инерции, в свою
очередь, являются следствием ускоренного
движения материальных объектов при
наличии неоднородного поля кинетической
энергии. Такое поле и существует во
вращающихся вокруг ядра электронах.
Значит, и электроны должны деформироваться
при своем вращении вокруг ядра атома и
при вращении вокруг своей оси.
Интересно
отметить, что при прямолинейном движении
тел с постоянным ускорением градиента
скорости по их длине в направлении
движения не будет, хотя на них и будут
действовать силы инерции. Такое положение
как раз и объясняется тем, что действие
сил инерции перемещается на микрочастицы,
из которых состоит тело. Результирующая
же сила инерции, действующая на тело в
целом, будет представлять собой сумму
микроинерционных сил, действующих на
каждый электрон.
Потенциальная
энергия также будет являться следствием
действия микроинерционных сил,
обусловленных движением микрочастиц
в пространстве, поэтому можно утверждать,
что потенциальная энергия является
свойством кинетической энергии тела,
но не на макро, а на микроуровне его
структурной организации, которая,
однако, зависит от скорости изменения
кинетической энергии при движении всего
тела в целом, то есть от действующей на
него внешней силы. В этом и будет
заключаться физическая сущность
потенциальной энергии.
На первый
взгляд может показаться, что такое
определение потенциальной энергии
будет справедливо только при упругих
деформациях тел, но не может характеризовать
физической сущности потенциальной
энергии, например, поля тяготения.
Однако, это не так. Ниже нами будет
показано, что силы тяготения могут быть
объяснены упругими деформациями частиц
вакуума, с движением которых связано
существование поля кинетической энергии,
через посредство которого и могут быть
найдены эти силы. То же самое можно
сказать и о других видах потенциальной
энергии, возникающей при взаимодействии
материальных объектов.
22. Связь между потенциальной энергией и силой(формула с градиентом).
Каждой
точке потенциального поля соответствует,
с одной стороны, некоторое значение
вектора силы
действующей
на тело, и, с другой стороны, некоторое
значение потенциальной энергии
![]() .
Следовательно, между силой и потенциальной
энергией должна существовать определенная
связь.
.
Следовательно, между силой и потенциальной
энергией должна существовать определенная
связь.
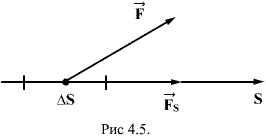 Для
установления этой связи вычислим
элементарную работу
Для
установления этой связи вычислим
элементарную работу
![]() ,
совершаемую силами поля при малом
перемещении
,
совершаемую силами поля при малом
перемещении
![]() тела,
происходящем вдоль произвольно выбранного
направления в пространстве, которое
обозначим буквой
.
Эта работа равна
тела,
происходящем вдоль произвольно выбранного
направления в пространстве, которое
обозначим буквой
.
Эта работа равна
![]() где
где
![]() -
проекция силы
на
направление
.Поскольку
в данном случае работа совершается за
счет запаса потенциальной энергии
,
она равна убыли потенциальной энергии
-
проекция силы
на
направление
.Поскольку
в данном случае работа совершается за
счет запаса потенциальной энергии
,
она равна убыли потенциальной энергии
![]() на
отрезке оси
:
на
отрезке оси
:
![]()
Из двух последних выражений получаем
![]()
Откуда
![]()
Последнее выражение дает среднее значение на отрезке . Чтобы
получить значение в точке нужно произвести предельный переход:
![]()
Так как может изменяться не только при перемещении вдоль оси , но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от по :
![]()
Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:
![]()
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:
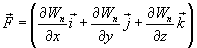
в
математике вектор
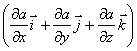 ,
,
где
а - скалярная функция х, у, z, называется
градиентом этого скаляра обозначается
символом
![]() .
Следовательно
сила равна градиенту потенциальной
энергии, взятого с обратным знаком
.
Следовательно
сила равна градиенту потенциальной
энергии, взятого с обратным знаком
|
23. Полная механическая энергия
Полная механическая энергия - сумма кинетической и потенциальной энергии тела.