
- •14.Модель вязко-упругого тела Кельвина-Фойгта
- •Факторы, влияющие на коэффициент спрессованности тетрадей
- •17. Этапы склеивания. Смачивание и прилипание
- •18 Теории адгезии и склеивания
- •19 Оценка технологических свойств клеев
- •20. Факторы, определяющие прочность и долговечность клеевых соединений
- •21. Старение клеевых соединений
- •22. Факторы, влияющие на качество блоков в процессе заклейки, сушки и обжима корешка
- •23. Понятие подобия явлений и процессов. Виды подобия.
- •23.Инварианты и критерии подобия.
- •25. Анализ размерностей
- •27. Аналитический метод получения обобщенных переменных
27. Аналитический метод получения обобщенных переменных
Ниже излагаются основы теории подобия, предложенные А. Н. Колмогоровым Предположим, что для описания изучаемых явлений используют т основных (первичных) независимых единиц измерения А1, А2, ... (например, единицы длимы L, массы М и времени Т). Производные единицы измерения образуются из основных согласно соотношению
 . (4
.6)
. (4
.6)
Их размерность характеризуется числовыми показателями p1, p2, ….pm. Каждая величина X размерности [X] = [Q] представляется в виде X = xQ (где x - числовое выражение величины X при выбранной системе основных величин).
Пусть изучается класс явлений S и пусть каждое из них определяется заданием некоторой системы величин У. Два таких явления S1 и S2 называют подобными, если значения величин У2, характеризующих явление S2, получаются из значений соответствующих величин У1, характеризующих явление S1, по формуле
 (4.7)
(4.7)
где коэффициенты подобия к1, к2, ... , кт постоянны, а показатели р1, р2, ... , рм определяются размерностью величин У:
 (4.8)
(4.8)
Предположим, что из системы величин У выделена некоторая часть, образующая систему определяющих параметров X, так что численное значение у любой величины У является функцией
у=f(X), численное значение х-параметров X, а вид функциональных зависимостей остается одними тем же при любом выборе основных
единиц измерения А1, А2
….Аь. При таком предположении основной принцип теории подобия может быть сформулирован следующим образом: для подобия явлений S1 и S2 необходимо и достаточно, чтобы значения любой безразмерной комбинации определяющих параметров
 (4.9)
(4.9)
в явлениях Si и S2 были равны, т.е. к1 = к2 .
Каждое безразмерное выражение к вида (4.9) называют критерием подобия. Очевидно, что при таком определении критериев подобия в их число попадают все безразмерные определяющие параметры и все соотношения вида
(4.10)
k= Х{/Х2,
где Х1 и Х2 – определяющие параметры одной и той же размерности.
Необходимость для подобия равенств k1
= k2 в
применении к безразмерным параметрам
и отношениям вида (4.10) очевидна. Их можно
называть тривиальными (симплексными).
Отношения к вида (4.10) при перечислении
критериев подобия часто опускают. Если
тривиальные условия подобия к1
= к2 считаются заведомо
выполненными, то среди нетривиальных
условий подобия k1
= k2
имеется только s=
n — т1 независимых (где
n -число различных
размерностей величин системы
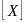 ,
т1 -число независимых
размерностей среди этих п). Поскольку
всегда mt
,
т1 -число независимых
размерностей среди этих п). Поскольку
всегда mt
 т, S
n. — т.
т, S
n. — т.
Если исследуемые явления изучают с помощью дифференциальных уравнений, то определяющие параметры появляются либо в виде величин, входящих в начальные и граничные условия, либо в виде коэффициентов, входящих в дифференциальные уравнения. После приведения уравнений к безразмерному виду в них остаются безразмерные коэффициенты, которые и являются критериями подобия.
Таким образом, рассмотренный аналитический метод получения обобщенных с переменных-критериев подобия - объединяет основы теории подобия с анализом размерностей и определяет необходимые и достаточные условия получения обобщенных критериальных уравнений любого процесса, для которого составлено математическое описание.
