1.Мн-ва: понятие мн-ва, способы задания мн-ва.ю операции над мн-вами.

Множество-это совокупность объектов той или иной природы обладающих общим признаком и рассматриваемых как целое. Объекты входящие в состав множества наз. элементами этого мн-ва.

Способы задания мн-в.

1.Мн-во можно задать указанием характеристического св-ва, то есть такого свойства которым обладает все элементы данного мн-ва.2.Если число элементов мн-ва конечно то мн-во можно задать простым перечислением его элементов.

Мн-во считается заданным если относительно каждого объекта можно сказать пренадлежит он данному мн-ву или нет. Если мн-во не содержит ни одного элемента, то его называют пустым.

Операции над мн-вами.

Два множества A и B наз. равными если они состоят из одних и тех же элементов.

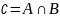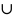1.Пересечение мн-в A и B наз. мн-во элементы которого принадлежат и мн-ву А и мн-ву В. 2.Объединением мн-в А и В наз. мн-во С который обозначается , элементы которого принадлежат хотя бы одному мн-ву А или В.3. Разностью мн-в А и В наз. С=А\В элементы которого принадлежат мн-ву А, но не принадлежат мн-ву В.4.Если все операции над мн-вом осуществляется внутри некоторого мн-ва Т, то Т наз. универсальным или основным мн-вом. Тогда если АсТ, то Т\А= наз. дополнением мн-ва А.

2.Основные числовые мн-ва, примеры. Вещественные числа.

Вещественные числа

1.Мн-во натуральных чисел( N={1,2,3,..}).2.мн-во целых чисел.(Z={0,±1,± 2,±3,..})3. мн-во рациональных чисел.(Q={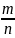 | mєz, nєz, n≠0}4. мн-во R бесконечных десятичных дробей наз. мн-вом вещественных чисел.(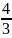 =1,333..)

Замечание. если дробь конечна, то сделать ее бесконечной можно 2 способами.

Вещественные числа не являющиеся рациональными являются иррациональные. Два вещественных числа а=±а0,а1,а2,…аn,… в=±в0,в1,в2,…,вn,… называются равными если они имеют одинаковые знаки и справедливо бесконечная цепочка равенств.а0=в0, а1=в1, а2=в2,…, аn= вn.

3.Ограниченные и неограниченные числовые мн-ва, точные верхние и нижние грани мн-тв; теорема о существовании точной верхней(нижней) грани у ограниченного сверху(снизу) мн-ва.

Мн-ва вещественных чисел ограниченных сверху или с низу.

Опр. Мн-во х наз. сверху (снизу) если найдется такое число М(м) что для всех элементов хЄХ выполняется неравенство х≤М(х≥м). М наз. верхней гранью мн.х , м- нижней гранью. Замечание очевидно что если мн-во ограниченно сверху то оно имеет бесконечно много верхних граней, а если мн-во ограниченно снизу то оно имеет бесконечно много нижних граней.

Опр. Наименьшее из всех верхних граней ограниченного сверху мн-ва наз. точной верхней гранью этого мн-ва. Наибольшая из всех нижних граней ограниченного снизу мн-ва наз. точной нижний гранью этого мн-ва. Таким образом точная верхняя и точная нижняя грани может как и принадлежать так и не принадлежать рассматриваемого мн-ва.

Теорема. Если некоторое мн-во Х ограниченное сверху(снизу), то найдется такое вещественное число 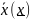, которое является точной верхней (нижней) гранью.

Опр. мн-во х наз. ограниченным если оно ограниченно и сверху и снизу т.е. если найдутся такие вещественные числа М и м, что для любого элемента из мн-ва выполняется неравенства м≤х≤М.

Следствие Если мн-во ограниченно то оно имеет точную верхнюю и точную нижнюю грань.

4.Числовые последовательности: понятие числовой последовательности, операции над ними, ограниченные и неограниченные последовательности, бесконечно большие последовательности;примеры. Числовые последовательности и операции над ними.

Опр.1. Если каждому значению n натурального ряда чисел 1,2,3,... поставлено в соответствии по определенному закону некоторое число 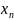, то мн-во занумерованных чисел 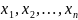.. наз. числовой последовательностью. Числа наз. элементами этой последовательности -общий член этой последовательности.

Опр.2. числовая последовательность 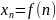, т.е. числовая последовательность это f:N→R.

Числовая последовательность это функция которая переводит мн-во натуральных чисел во мн-во вещественных.

Ограниченные, неограниченные, бесконечно-большие посл-ти.

Опр. Посл-ть наз. ограниченной сверху(снизу) если найдется такое число М(м) такое, что для любого элемента выполняется неравенство ≤М ( ≥м).

М верх. Грань, м- нижняя грань.

Замечание ограниченная сверху пос-ть имеет бесконечно много верхних граней, ограниченная снизу пос-ть имеет бесконечно много нижних граней.

Опр. пос-ть наз. ограниченной если она ограниченна с обеих сторон, т.е м≤х≤М. для любого элемента посл-ти.

Пос-ть не являющаяся ограниченной наз. неограниченной, т.е. посл-ть наз. неограниченной если любое А>0найдеться элемент такой что выполняеться неравенство | |>A.

Опр. Пос-ть наз. бесконечно-большой если любое А>0 найдеться номер N для всех элементов с номерами n≥N выполняется неравенство |>A.Очевидно, что любая бесконечно-большая пос-ть является неограниченной, но из неограниченной пос-ти не следует, то что она является бесконечно-большой.

5.Бесконечно-малые посл-ти и их св-ва Опр. Пос-ть {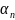 } наз. бесконечно-малой, если любой ε>0 найдется N, такой что для всех элементов с номерами n≥N выполняется неравенство | |< ε.

Св-ва бесконечных посл-тей.

Теорема 1. {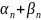 } и {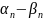 } двух бесконечно малых пос-тей также является бесконечной малой пос-ю.

Следствие. Сумма любого конечного числа бесконечно малых пос-тей также являеться бесконечно малой пос-тью.

Теорема2. Произведение {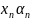 } ограничены пос-тью на бес.-мал. Пос-ть также является бес.-мал. Пос-тью.

Теорема3 любая бес.-мал. Пос-ть является ограниченной.

Следствие. Произведение любого конечного числа бес.-мал. Пос-ти также является б.м. пос-тью

Замечание. Частное двух б.м. пос-тей может быть пос.тью любого типа , а может даже не иметь смысла.

Теорема4. Если все элементы б.м. пос-ти { } равны по одному и тому же числу с то с=0.

Теорема5. Если с б.б. пос-ть то начиная с некоторого номера определенна пос-ть {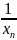 } которая является б.м.

Если все элементы б.м .{ }пос-ти отличны от нуля то определена пос-ть которая является бес. Большой.