
- •2.Основные числовые мн-ва, примеры. Вещественные числа.
- •3.Ограниченные и неограниченные числовые мн-ва, точные верхние и нижние грани мн-тв; теорема о существовании точной верхней(нижней) грани у ограниченного сверху(снизу) мн-ва.
- •6.Сходящиеся посл-ти: определение предела посл-ти, основные св-ва сходящихся посл-тей. Сходящиеся пос-ти.
- •8.Понятие ф-ции. Область определения, мн-во значений, способы задания. Простейшие элементарные ф-ции. Понятия функции.
- •9.Предел ф-ции в точке: определение предела ф-ции по Каши и по Гейне, эквивалентность двух определений. Предел функций.
- •10.Односторонние пределы. Св-ва ф-ций, имеющих предел: арифметические операции, предельный переход в неравенствах. Понятие одностороннего предела.
- •14.Точки разрыва, их классификация, примеры.
6.Сходящиеся посл-ти: определение предела посл-ти, основные св-ва сходящихся посл-тей. Сходящиеся пос-ти.
Опр1.
Пос-ть{
}наз.
сходящийся если найдется такое
вещественное число а, что пос-ть { }
является бесконечной малой. Число а
наз. пределом пос-ти {
}и
обозначается
}
является бесконечной малой. Число а
наз. пределом пос-ти {
}и
обозначается
 или
→a
при n→∞/
или
→a
при n→∞/
Замечание. Любая юесконечно-малая пос-ть является сходящийся с а=0.
Св-ва сходящихся пос-тей.
1.Сходящиеся
пос-ть имеет только один предел. 2. Любая
сходящиеся плоскость ограничена.
Замечание. Из ограниченности пос-ти
сходимость не следует.3. Сумма {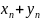 },
разность {
},
разность { },произведение
{
},произведение
{ }
и частное {
}
и частное {
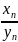 }(y
не равен 0) сходящиеся пос-тей {
}(y
не равен 0) сходящиеся пос-тей { }
имеющих своими пределами число а и в
являются сходящимися пос-тями имеющими
пределы соответственно равны а+в, а-в,
а*в, а\в(в не равно 0).4. если пос-ть
{
}сходиться
к некоторому числу х, по крайне мере с
некоторого номера выполняется неравенство
≥а(
≤в),
то х≥а(х≤в).
}
имеющих своими пределами число а и в
являются сходящимися пос-тями имеющими
пределы соответственно равны а+в, а-в,
а*в, а\в(в не равно 0).4. если пос-ть
{
}сходиться
к некоторому числу х, по крайне мере с
некоторого номера выполняется неравенство
≥а(
≤в),
то х≥а(х≤в).
Замечание. Если >a( <b), то не следует отсюда x>a(x<b)
7.монотонные посл-ти, теорема(признак Вейерштрасса) о сходимости монотонных ограниченных посл-тей. Опр. Посл-ть наз. Монотонной если она является неубывающей ( невозрастающей ).Теорема: для сходимости монотонной посл-ти необходимо и достаточно чтобы она являлась ограниченной. Замеч.- и любая сходящиеся пос-ть является монотонной. Пример(1,-1/2,1/3,-1/4,….,1/2n-1,-1/2n;) сходиться к 0 но не является монотонной.
8.Понятие ф-ции. Область определения, мн-во значений, способы задания. Простейшие элементарные ф-ции. Понятия функции.
Опр. Если каждому числу х из некоторого мно-ва поставлено в соответствии по определенному закону некоторое число у, то говорят что на мн-ве х задана функция у=у(х).
Х-наз. аргументом или независимой переменной. Х- наз. областью определения функции, у- наз. частным значением функции в точке х.
Спосабы
задания ф-ции: 1 по средствам формул.
2.табличные способ- заключаються в
задание таблицы отдельных значений
аргумента и соответствующих им значении
ф-ций. 3.графический способ- соответствии
между аргументом и ф-ции задается по
средстом графики. Простейшие элементарные
ф-ци. 1 Степенная ф-ция y=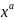 2.показательная ф-ции y=
2.показательная ф-ции y=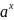 a>0,
a≠1.
3Логорифмическая ф-ция y=
a>0,
a≠1.
3Логорифмическая ф-ция y= ,
a>0,
a≠1.
Тригонометрические ф-ции: y=
,
a>0,
a≠1.
Тригонометрические ф-ции: y= ,
y=
,
y= ,
y=tgx,
y=ctgx.
5.Обратные тригонометрическиеф-ции
y=arcsinx,
y=arccosx,
y=arctgx,
y=arcctgx.
,
y=tgx,
y=ctgx.
5.Обратные тригонометрическиеф-ции
y=arcsinx,
y=arccosx,
y=arctgx,
y=arcctgx.
9.Предел ф-ции в точке: определение предела ф-ции по Каши и по Гейне, эквивалентность двух определений. Предел функций.
Опр. Предел функций по гейне.
Число
b
наз.пределом функции y=f(x)
в точке а, если для любой пос-ти значений
аргумента
..
сходящиеся к а, и состоящая из чисел
не
равно а, соответствующая пос-ть значений
функции f(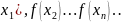 сходится
к числу b
сходится
к числу b
Опр. Предел функции по Каши.
Число b наз.пределом функции y=f(x) в точке а, если для любого положительного числа найдется число положительное, такое что для всех значений аргумента ч, удовлетворяющих неравенство 0<|x-a|<δ выполняется неравенство |f(x)-b|<ε
10.Односторонние пределы. Св-ва ф-ций, имеющих предел: арифметические операции, предельный переход в неравенствах. Понятие одностороннего предела.
Опр. По гейне.
Число
b
наз. правым(левым) пределом функции
y=f(x)
в точке а, если для любой пос-ти
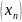 значений аргумента, сходящиеся к а и
состоящий из чисел >a,
соответствующая пос-ть {
значений аргумента, сходящиеся к а и
состоящий из чисел >a,
соответствующая пос-ть { }
значение функции сходится к b
}
значение функции сходится к b
Опр. По каше.
Число b наз. правым(левым) пределом функции y=f(x) в точке а, если любое ε>0 найдется число δ>0, такое что для всех значений аргумента х из интервала в случ. Предела (а,а+б)( в случ. Лев. Пр. (а-б, а)) выполняется неравенство |f(x)-b|<ε
Арифметические операции над функциями имеющими предел.
Теорема пусть 2 функции f(x) и g(x)заданы на одном и том же множестве х, и имеют в точке а пределы равные соответственно b и c. тогда функции f(x) +- g(x), f(x)*g(x), f(x)\g(x) имеют в точке а пределы, равные соответственно b+-c,b*c,b\c(c≠0)
Предельный переход в неравенствах. Теорема: Если 3 ф-ции, f(x), h(x), g(x) заданные в некоторой проколотой окрестности т.а две из которых f(x) и g(x) имеет одинаковый предел b и всюду в этой окрестности выполняется неравенство f(x)≤h(x)≤g(x) то очевидно что ф-ции h(x) так же имеет предел в т.а то ф-ция h(x) имеет в т.а предел так же равный b.
11.«Замечательные»
пределы. Первый замечательный предел.
Второй замечательный предел.(две формы
записи). .1-й
замечательный предел: Предел ф-ции
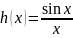 в точке x=0
существует и равен 1.
в точке x=0
существует и равен 1.
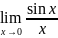 =1
=1
2-ой
зам. Предел: предел ф-ции
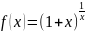 в точке x=0
существует и равен e.Следствие:
Предел при
в точке x=0
существует и равен e.Следствие:
Предел при
 ф-ции
существует и равен e.
ф-ции
существует и равен e.
 =e.
=e.
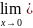 .
.
12.Бесконечно
малые ф-ции, сравнение бесконечно малых
ф-ции, примеры. .опр.
ф-ция α(x)
наз. беск. Малой в точке а, если
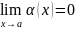 .
Замечание: если известно, что
.
Замечание: если известно, что
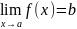 ,
то f(x)-b=
α(x).
,
то f(x)-b=
α(x).
Сравнение:
Пусть α(x)
и β(x)
– б.м. в т.а ф-ции. 1.ф-ция α(x)
является б.м. высокого порядка в т.а ,
чем β(x)
если
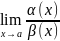 =0.
Пример: α(x)=
=0.
Пример: α(x)= β(x)=
β(x)=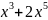 в т.х=0
в т.х=0
 =
=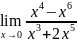 =
= =
= обозначение: α=0(β) 0-б.м. более высокого
порядка.
обозначение: α=0(β) 0-б.м. более высокого
порядка.
2.
Ф-ции α(x)
и β(x)
являются в т.а б.м. одного порядка, если
≠0≠∞
пример: α(x)=
β(x)=7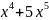 в т.х=0
=
в т.х=0
=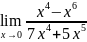 =
= =
=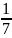 .
.
3.
Ф-ции α(x)
и β(x)
являются в т.а эквивалентными б.м. если
=1.
α(x)~β(x).
Пример: α(x)= -
б.м. в т.х=3 β(x)=
-
б.м. в т.х=3 β(x)=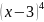
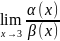 =
= =
=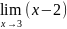 =1.
Если ф-ции α(x)~β(x)
то при то при решении пределов одну
ф-цию можно заменить другой.
=1.
Если ф-ции α(x)~β(x)
то при то при решении пределов одну
ф-цию можно заменить другой.
13.Два
определения непрерывности ф-ции в точке.
Арифметические операции над ф-циями,
непрерывными в точке. Сложная ф-ция и
ее непрерывность. Непрерывность на
мн-ве. опр.
ф-ция
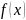 наз.
непрерывной в точке а если существует
предел ф-ции
в точке а, причем этот предел равен
частному значению
наз.
непрерывной в точке а если существует
предел ф-ции
в точке а, причем этот предел равен
частному значению
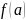 ф-ции в этой точке
ф-ции в этой точке
 .
опр. ф-ция
наз.
непрерывной на множестве х если она
непрерывна в каждой точке этого множества.
Опр. ф-ция
наз.
непрерывной в точке а с права(с лева)
если существует правый(левый) предел
в точке а, равный частному значению
ф-ции в этой точке. утв. Если ф-ция
непрерывна с права и с лева в точке а то
эта ф-ция и просто непрерывна в точке
а.
.
опр. ф-ция
наз.
непрерывной на множестве х если она
непрерывна в каждой точке этого множества.
Опр. ф-ция
наз.
непрерывной в точке а с права(с лева)
если существует правый(левый) предел
в точке а, равный частному значению
ф-ции в этой точке. утв. Если ф-ция
непрерывна с права и с лева в точке а то
эта ф-ция и просто непрерывна в точке
а.
