3 Раздел. Интегральное исчесление функций одной переменной.

1. Первообразная и неопределенный интеграл. Таблица интегралов.

Первообразная.

Ф-я F(x) называется первообразной ф-и f(x) на множестве D, если для любого х из D:F’(x)=f(x).

Если F(x) первообрзная ф-и f(x) на мн-ве D, то любую другую первообразную этой ф-и можно получить по формуле: Ф(х)=F(x)+c при некотором значение с.

Неопределенный интеграл и его св-ва.

Опр. Совокупность всех первообразных для ф-и f(x) на множестве наз. Неопределенным интегралом этой функции. ?f(x)dx=F(x)+c, f(x)-подинтегральная ф-я ,f(x)dx – подинтегральное выражение.

Таблицу интегралов от руки.

   Простейшие интегралы

2. Общее правило интегрирования.

3.Замена переменной в неопределенном интеграле.

При решении задач замену переменной можно выполнить двумя способами. 1. Если в подынтегральной функции удаётся сразу заметить оба сомножителя, и f(t(x)), и , то замена переменной осуществляется подведением множителя под знак дифференциала: , и задача сводится к вычислению интеграла .

2. Замену переменной можно осуществлять формальным сведением подынтегрального выражения к новой переменной

4. Интегрирование по частям в неопределенном интеграле.

Интегрирование по частям - приём, который применяется почти так же часто, как и замена переменной. Пусть u(x) и v(x) - функции, имеющие непрерывные частные производные. Тогда по формуле дифференцирования произведения d(uv) = u∙dv + v∙du . Находим неопределённые интегралы для обеих частей этого равенства (при этом ): . Эта формула и называется формулой интегрирования по частям. Часто ее записывают в производных (dv = v’∙dx , du = u’∙dx):

5. Схема разложения правильной рациональной дроби на элементарные.

Лемма 1. Пусть правильная дробь и a – вещественный корень многочлена Q(x), т.е. Q(x)=(x-a)Q1(x), Q1(a)0,1. Тогда существует A и многочлен P1(x) такие, что

 ,

где - правильная дробь.

Доказательство:  Рассмотрим разность (A - некоторое, пока неопределенное число)

.

Дробь справа правильная, так как порядок P(x) и AQ1(x) меньше порядка знаменателя. Положим , тогда для числителя число a будет корнем P-AQ1=(x-a)P1(x), что и требовалось доказать.

Лемма 2. Пусть правильная дробь и w=u+iv (v0) – комплексный корень многочлена Q(x), т.е. Q(x)=(x2+px+q)Q1(x), Q1(w)0, 1. Тогда существуют вещественные числа M, N и многочлен P1(x) с вещественными коэффициентами  такие, что

 ,

где - правильная дробь.

6.Опеределенный интеграл как предел интегральных сумм.

Пусть на отрезке [a,b] задана функция y = f(x). Разобьём отрезок [a,b] произвольным образом на n частей точками [x0 , x1], [x1 , x2], …, [xi-1 , xi], …, [xn-1 , xn]; длину i-го отрезка обозначим : ; максимальную из длин отрезков обозначим . На каждом из отрезков [xi-1 , xi] выберем произвольную точку и составим сумму . Сумма называется интегральной суммой. Если существует (конечный) предел последовательности интегральных сумм при , не зависящий ни от способа разбиения отрезка [a,b] на части [xi-1 , xi], ни от выбора точек , то функция f(x) называется интегрируемой по отрезку [a,b], а этот предел называется определённым интегралом от функции f(x) по отрезку [a,b] и обозначается 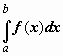. Функция f(x), как и в случае неопределённого интеграла, называется подынтегральной, числа a и b - соответственно, нижним и верхним пределами интегрирования. Кратко определение иногда записывают так: . В этом определении предполагается, что b> a. Для других случаев примем, тоже по определению: Если b=a, то ; если b<a, то .

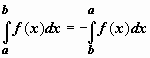7.Теорема об оценке определенного интеграла.

1.ли на отрезке [a,b] функция удовлетворяет неравенству , то . Док-во. Докажем левое неравенство (цифрами над знаками импликации обозначены номера применяемых ранее доказанных свойств): . Аналогично доказывается и правое неравенство. 2.сли функция f(x) интегрируема по отрезку [a,b], то . Док-во.

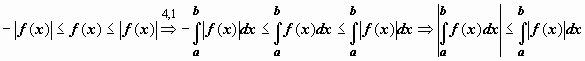
8. Теорема о среднем для определенного интеграла.

Если f(x) непрерывна на отрезке [a,b], то существует точка , такая что . Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка , такая что . Это свойство имеет простую геометрическую интерпретацию: если непрерывна на отрезке [a,b], то существует точка такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [a,b] и высотой f(c).

9.Определеный интеграл с переменным верхнем приделом.

Интеграл с переменным верхним пределом. Значение определённого интеграла не зависит от того, какой буквой обозначена переменная интегрирования: 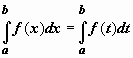этом разделе переменную интегрирования будем обозначать буквой t, а буквой x обозначим верхний предел интегрирования. Будем считать, что верхний предел интеграла может меняться, т.е. что x - переменная, в результате интеграл будет функцией Ф(x) своего верхнего предела: . Легко доказать, что если f(t) интегрируема, то Ф(x) непрерывна, но для нас важнее следующая фундаментальная теорема: Теорема об интеграле с переменным верхним пределом. Если функция f(t) непрерывна в окрестности точки t = x, то в этой точке функция Ф(x) дифференцируема, и . Другими словами, производная определённого интеграла от непрерывной функции по верхнему пределу равна значению подынтегральной функции в этом пределе.

10. Основная теорема интегрального исчисления. Формула Ньютона-Лейбница.

Формула Ньютона-Лейбница. Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции , то

11.Замена переменной в определенном интеграле.

1. определена, непрерывно дифференцируема и монотонна на отрезке ,

2. ,

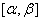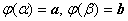3. функция непрерывна на отрезке [a, b].

Тогда

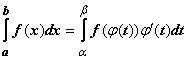
12. Интегрирование по частям в определенном порядке.

Если u(x), v(x) - непрерывно дифференцируемые функции, то .

12. Площадь плоской фигуры в декартовых координатах.

Если плоская фигура ограничена прямыми х=а, у=в (а<в) и кривыми у=у1(х), у=у2(х), причем у1(х) у2(х), (а х в), то ее площадь вычисляется по формуле

14. Площадь плоской фигуры в полярных координатах.

Площадь правильной области           в полярных координатах находится так:

   

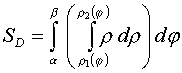
15.Объем тел при заданной площади поперечных сечений. Объем тел вращения.

Пусть имеется тело объема V. Площадь любого поперечного сечения тела Q, известна как непрерывная функция Q = Q(x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки хi разбиения отрезка [a, b]. Т.к. на каком- либо промежуточном отрезке разбиения [xi-1, xi] функция Q(x) непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно Mi и mi.

  Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны Mixi и mixi здесь xi = xi - xi-1.

  Произведя такие построения для всех отрезков разбиения, получим цилиндры, объемы которых равны соответственно  и .

  При стремлении к нулю шага разбиения , эти суммы имеют общий предел:

Таким образом, объем тела может быть найден по формуле:

  Недостатком этой формулы является то, что для нахождения объема необходимо знать функцию Q(x), что весьма проблематично для сложных тел.

Объём и площадь поверхности тел вращения можно узнать при помощи теорем Гульдина-Паппа

• Первая теорема Гульдина-Паппа гласит:

Площадь поверхности, образуемой при вращении линии, лежащей в плоскости целиком по одну сторону от оси вращения, равна произведению длины линии на длину окружности, пробегаемой центром масс этой линии.

• Вторая теорема Гульдина-Паппа гласит:

Объём тела, образуемого при вращении фигуры, лежащей в плоскости целиком по одну сторону от оси вращения, равен произведению площади фигуры на длину окружности, пробегаемой центром масс этой фигуры.

16. Длина дуги и и формула для ее вычисления , дифференциал дуги.

Длина дуги окружности L = A * R L = A * R Где L — длина дуги окружности, R — радиус окружности, A — центральный угол, выраженный в радианах (см. тригонометрические функции). Так, для окружности, A = 2*пи (360 градусов), получим L = 2*пи*R.

17.Площадь поверхности вращения.

Площадь поверхности вращения, образованной вращением плоской кривой конечной длины вокруг оси, лежащей в плоскости кривой, но не пересекающей кривую, равна произведению длины кривой на длину окружности с радиусом, равным расстоянию от оси до центра масс кривой. Это утверждение называется второй теоремой Гюльдена, или теоремой Паппа о центроиде.

Площадь поверхности ращения, образованной вращением кривой вокруг оси можно вычислить по формуле

Площадь поверхности вращения, образованной вращением кривой вокруг оси можно вычислить по формуле

Для случая, когда кривая задана в полярной системе координат действительна формула