Резонанс в цепях переменного тока.

Реактивные индуктивные и емкостные сопротивления цепи переменного тока могут полностью уравновесить друг друга. В этом случае имеем резонанс в цепи. При резонансе сопротивление цепи является чисто активным, угол сдвига между напряжением и током равен нулю и cosφ = 1. Резонанс в цепи можно получить тремя способами: изменяя частоту напряжения цепи, индуктивность или емкость или то и другое вместе. Угловая частота ω, при которой наступает резонанс, называется резонансной или собственной угловой частотой цепи ω_о .

1. Резонанс при последовательном соединении элементов цепи - резонанс напряжений. Напряжения на индуктивности и конденсаторе взаимно компенсируются и резонансная угловая частота ω_о определяется из условия:

U_L = U_c ; X_L = X_c ; ω_о L = 1/ ω_о C, откуда: ω_о = 1/ √LC.

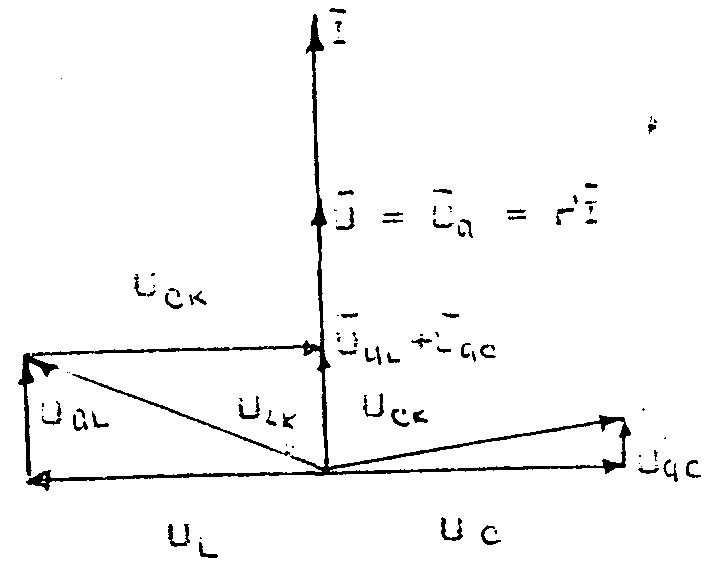
Рис. 14. Векторная диаграмма при резонансе напряжений.

Полное сопротивление цепи равно только активному сопротивлению цепи r = z. Ток в цепи при U = const. достигает наибольшего значения. Напряжение на зажимах катушки и конденсатора могут превосходить напряжение на зажимах цепи в десятки раз, поэтому резонанс при последовательном соединении называется резонансом напряжений. X_L = X_c = ω_о L = √L/C = Z - волновое сопротивление.

Q = U_L/U =U_c/U = ZI/rI = Z/r - добротность цепи.

2. Резонанс при параллельном соединении элементов цепи - резонанс токов. Резонанс токов наступает при равенстве реактивных проводимостей B_L и B_c:

ω_о L/{[r_L²] + (ω_о L)²} = (1/ ω_о C) {1/[r_c² + (1/ ω_о C)²]}.

При относительно малых r_L и r_c для резонансной частоты получаем выражение, подобное выражению при резонансе напряжений:

ω_о = 1/ √LC.

При резонансе проводимость цепи Y = g = g_l + g_c , угол φ = 0 и cosφ=1. Проводимость цепи имеет наименьшее значение, а ток минимален при неизменном напряжении цепи.

Рис. 15. Векторная диаграмма при резонансе токов.

Токи катушки и конденсатора могут превосходить общий ток цепи в несколько десятков раз не только при резонансе, но и с приближением к нему, поэтому резонанс при параллельном соединении элементов называется резонансом токов.

B_l = B_c = √^C/_L = γ - волновая проводимость.

γ = I_lk/U = I_ck/U. Отношение d = g/γ называется затуханием цепи.

Мощность цепи переменного тока.

Мгновенная мощность p = u i. Энергия, доставляемая в цепь, равна произведению времени, в течении которого энергия доставляется, на среднее значение мощности за рассматриваемый промежуток времени.

Средняя мощность за период:

P = (1/T) u i dt

При u = U_m sin ωt и i = I_m sin (ωt - φ)

P = (1/T) u i dt = (1/T) [ √2U sin ωt √2 I sin(ωt - φ)]dt =

= (UI/T) [cosφ - cos(2ωt - φ)] dt

Интеграл от 2-го члена равен нулю, поэтому: P = U I cos φ - средняя мощность за период, подобно мощности цепи постоянного тока, определяет энергию, подводимую к цепи за одну секунду. Поэтому ее называют активной мощностью. Значение мощности зависит от действующих тока и напряжения цепи и угла сдвига фаз между напряжением и током. U и I, множитель cos φ называется коэффициентом мощности.

Из выражения p = u i = U I [cos φ - cos (2ωt - φ)] следует, что мгновенная мощность цепи изменяется с удвоенной частотой 2ω; амплитуда изменения мощности равна UI.

1. Электрическая цепь с активным сопротивлением R.

cos φ = 1 и φ = 0; p = ui = UI (1 - cos 2ωt).

Средняя мощность Р равна произведению действующих напряжения и тока UI, наибольшее значение мощности равно 2UI, т.к. наименьшее значение cos 2ωt = -1, а наибольшее равно 1.

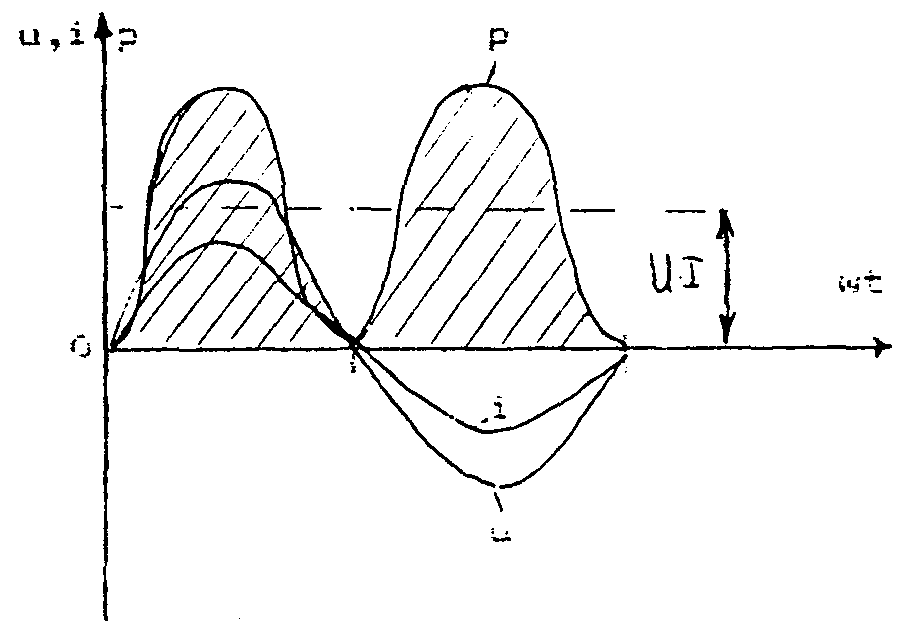
Рис. 16. Временная диаграмма напряжения, тока и мощности для цепи переменного тока с активным сопротивлением.

Заштрихованная площадь, ограниченная кривой мощности р и осью абсцисс, определяет pdt, т.е. электрическую энергию, преобразованную в тепловую за один период.

2. Электрическая цепь с идеальной индуктивностью L.

Ток отстает от напряжения на угол φ = π/2.

p = -UI cos (2ωt - π/2) = -UI sin 2ωt.

Средняя мощность равна нулю. Если переменный ток изменяется по гармоническому закону i = I_m sin (ωt - π/2) = -I_m cos ωt, то энергия магнитного поля W_m = (L i²) / 2 = { [ L (I_m)² ] / 2 } ( 1 + cos 2ωt ) / 2 также изменяется гармонически от O до LI² с угловой частотой 2ω. Мгновенная мощность цепи определяется скоростью изменения энергии магнитного поля:

p = ui = (d/dt) [(Li²)/2] = Li di/dt = -UI sin 2ωt

Рис. 17. Временная диаграмма напряжения, тока и мощности для цепи переменного тока с индуктивностью L.

При возрастании тока напряжение действует в направлении протекания тока, ЭДС самоиндукции действует в направлении навстречу току, при этом p = ui > 0, т.е. энергия поступает в цепь и преобразуется в энергию магнитного поля. При уменьшении тока напряжение действует в направлении, противоположном протеканию тока; ЭДС самоиндукции действует в направлении протекания тока; p = ui < 0 - энергия, запасенная в магнитном поле, - возвращается источнику. В цепи происходит непрерывный обмен энергией между источником энергии и цепью, с которой связано магнитное поле.