Векторные диаграммы.

Применение векторных диаграмм наглядно представляет рассматриваемые процессы и упрощает расчеты. Векторные диаграммы являются совокупностью векторов, изображающих действующие синусоидальные ЭДС и токи или их амплитудные значения. Гармонически изменяющееся напряжение определяется выражением:

u = U_m sin (ωt + ψ_u)

Под углом относительно оси Х изобразим вектор U_m, длина которого в масштабе равна амплитуде гармонической величины. Положительные углы будем откладывать в направлении против вращения часовой стрелки, а отрицательные - по часовой стрелке.

Предположим, вектор U с момента t = 0 вращается вокруг начала координат против часовой стрелки с постоянной частотой вращения ω, равной угловой частоте функции. В момент t. U_m повернется на угол ωt и будет расположен под углом ωt + ψ_u по отношению оси абсцисс.

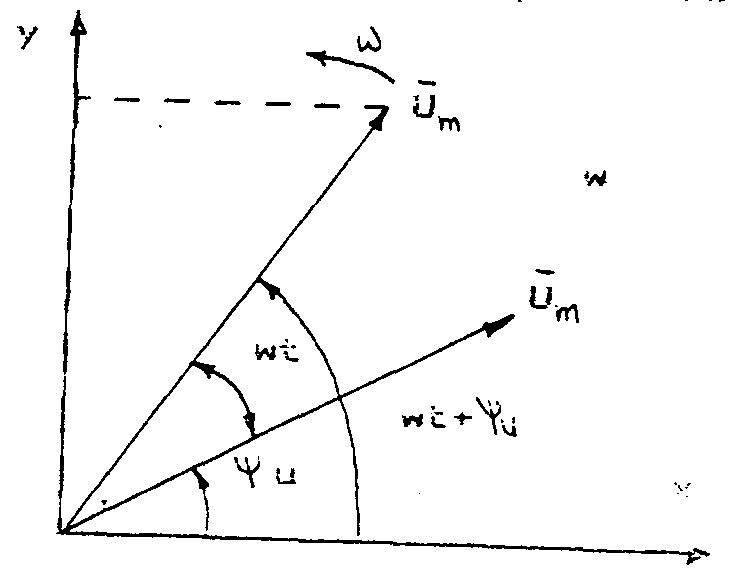
Рис. 8. Векторная диаграмма.

Его проекция на ось ординат равна мгновенному значению изображаемой функции u = U_m sin (ωt + ψ_u). Следовательно, величину, изменяющуюся гармонически во времени, можно изображать вращающимся вектором.

График зависимости любой переменной величины от времени называется временной диаграммой.

При расчетах требуются действующие ЭДС, напряжения и токи или амплитуды и их сдвиг по фазе. Поэтому рассматриваются неподвижные векторы для некоторого момента времени, который выбирается так, чтобы диаграмма была наглядной – векторная диаграмма.

Сложение Е, I или U одной и той же частоты можно осуществить аналитически и графически с помощью векторов Е_m = Е_1m + Е_2m.

Лекция 5

Тема: Электрические цепи синусоидального переменного тока.

В состав простых цепей переменного тока входят резисторы, катушки индуктивности, конденсаторы и элементы, соединенные магнитной или емкостной связью с другими цепями.

В резисторах электроэнергия полезно преобразуется в другие виды энергии или рассеивается как тепловая. Резистивный элемент характеризуется сопротивлением. Любой из них обладает некоторой индуктивностью и емкостью. Влиянием L и С можно иногда пренебречь. Если влиянием L пренебречь нельзя, то на схеме изображается последовательное соединение сопротивления и индуктивности. Реальный L-элемент обладает кроме L и R. Иногда надо учитывать влияние емкости. Индуктивность L линейного элемента в генри (Гн) определяется отношением потокосцепления Ψ в веберах (Вб) к току I в амперах (А):

L = Ψ/I, ом с.

Взаимная индуктивность М в генри между цепями 1 и 2 определяется отношением потокосцепления Ψ₁₂ или Ψ₂₁ цепи 1 или 2 в веберах к току цепи 2 или 1 соответственно:

M = Ψ₁₂/I₂ = Ψ₂₁/I₁

В реальной емкости имеются некоторые потери энергии. Поэтому С элемент надо изображать в виде параллельного соединения емкости С с проводимостью g. Потери энергии чаще всего невелики, поэтому С элемент изображается в виде идеальной емкости. Емкость С в фарадах определяется отношением заряда Q в кулонах к напряжению U:

С = Q / U.

Процессы в цепях переменного тока принципиально отличаются от процессов в цепях постоянного тока, I и U которых неизменны, при этом не изменяются электрические и магнитные поля, связанные с цепью. В цепях переменного тока при изменениях U и I изменяются магнитные и электрические поля, связанные с цепью. Возникают ЭДС самоиндукции и взаимоиндукции, протекают зарядные и разрядные токи.

Основные физические законы сформулированы применительно к цепям постоянного тока. Но они справедливы и к цепям переменного тока, но только для реально существующих в каждый момент мгновенных значений величин. На основе выражений, составленных по этим законам для мгновенных значений, составляются уравнения и формулируются законы для векторов и изображений напряжений, ЭДС и токов в символическом виде. В цепях переменного тока также показываются условные положительные направления ЭДС, U и I.

1. Электрическая цепь переменного тока с активным сопротивлением R. Пренебрегаем очень малой L и С проводов цепи. Сопротивление переменному току будет больше сопротивления постоянному току за счет неравномерного распределения тока в проводе и потерь энергии в окружающей среде. Поэтому в отличие от сопротивления постоянного тока сопротивление в цепи переменного тока называется активным.

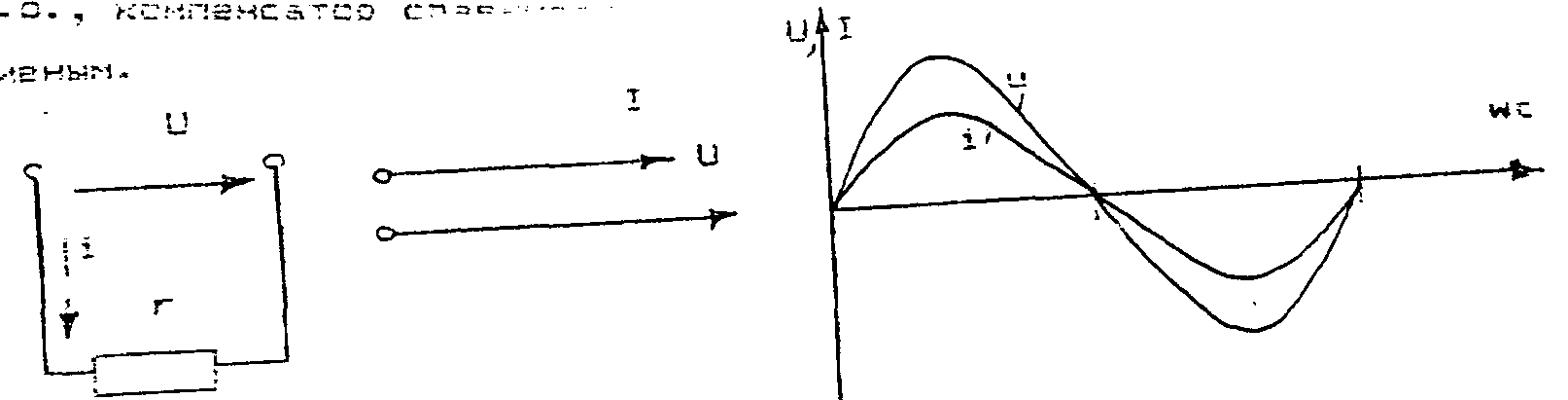
Рис. 9. Электрическая схема, векторные и временные диаграммы напряжения и тока для электрической цепи с активным сопротивлением.

По закону Ома:

i = u/r = (U_m/r) sin ωt = I_m sin ωt,

где I_m = U_m/R - амплитуда тока.

Действующие напряжение и ток меньше амплитудных значений в √2 раз; следовательно I = U/r и I = U/r

Ток и напряжение для цепи только с R совпадают по фазе. (Реостаты, электрические лампы, нагревательные приборы и др.).

2. Электрическая цепь переменного тока с индуктивностью L. Рассмотрение элемента цепи с сосредоточенными параметрами, обладающего только L, является научной абстракцией.

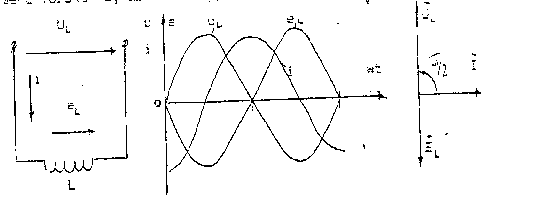
Рис. 10. Электрическая схема, векторные и временные диаграммы напряжения и тока для электрической цепи с индуктивным сопротивлением.

Изменение тока в цепи с L вызывает возникновение ЭДС самоиндукции е , которая по закону Ленца противодействует изменению тока. При увеличении тока е действует навстречу току, а при уменьшении - в направлении тока, противодействуя его уменьшению.

Для тока: i = I_m sin ωt и при L = const:

E_L = - L di/dt = - ωL I_m cos ωt = - E_Lm cos ωt = E_Lm sin(ωt - π/2)

где Е_Lm = ω L I_m - амплитуда ЭДС самоиндукции.

ЭДС самоиндукции отстает по фазе от тока на угол π/2. Чтобы в цепи протекал ток, требуется иметь на зажимах напряжение, уравновешивающее ЭДС самоиндукции, равное ей по значению и противоположное по знаку:

u = - E_L = L di/dt = ω L I_m cos ωt = U_Lm sin (ωt + π/2),

где U_Lm = ω L I_m - амплитуда напряжения. Для действующих тока и напряжения получаем выражения, аналогичные по форме закону Ома: U_L=ωLI и I = U_L/(ωL).

Величина ωL измеряется в Омах и называется индуктивным сопротивлением. Оно пропорционально частоте:

X_L = ωL = 2π f L.

3. Электрическая цепь переменного тока с емкостью С. Рассмотрение элемента цепи только с С также является научной абстракцией.

В цепи с идеальной С, включенной на напряжение переменного тока, происходит непрерывное перемещение электрических зарядов.

При увеличении напряжения ток в цепи конденсатора будет зарядным, а при уменьшении - разрядным. Мгновенный ток i равен скорости изменения заряда конденсатора:

i = dQ/dt = C du /dt,

где Q - заряд конденсатора, С - емкость конденсатора.

Рис. 11. Электрическая схема, векторные и временные диаграммы напряжения и тока для электрической цепи с емкостным сопротивлением.

Напряжение Uс на зажимах определяется отношением заряда Q к емкости С:

u_c = Q/C = ∫dQ/C = ∫i dt/C.

Если U_c = U_cm sin ωt, ток i будет равен:

i = C du/dt = ω C U_cm cos ωt = I_m sin(ωt + π/2)

Величина 1/ωC измеряется в Омах и называется емкостным сопротивлением X_c = 1/ωC = 1/2πfC и оно обратно пропорционально частоте приложенного напряжения. Действующее значения:

U_c = 1/ωC = x_c I, I = ω C U_c = U_c/x_c.

В цепи с конденсатором ток опережает напряжение на угол π/2.

4. Электрическая цепь с последовательным соединением активного сопротивления R, индуктивности L и емкости С. Рассматриваем идеализированную цепь с сосредоточенными параметрами.

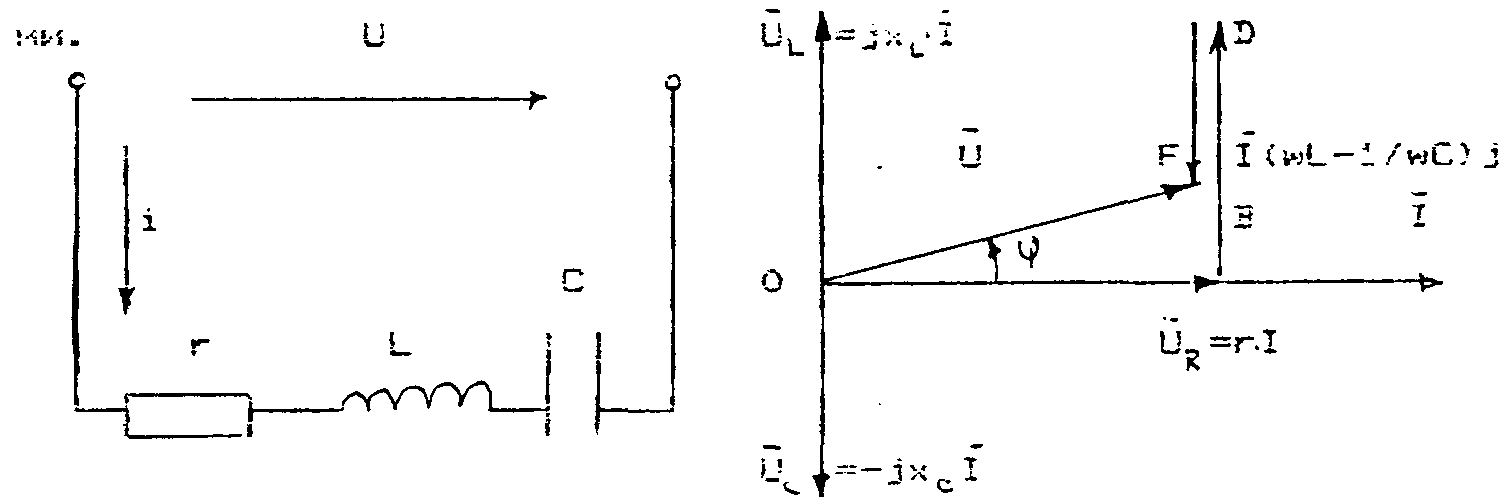
Рис. 12. Электрическая схема и векторные диаграммы напряжения и тока для электрической цепи с последовательным соединением R,L,C.

При u = U_m sin (ωt + ψ_u) ток будет равен i = I_m sin (ωt + ψ_i)

По 2-му закону Кирхгофа i r = u + E_L + E_c = u - L di/dt + ∫i dt/C, т. е.

U = U_q + U_L + U_c = i r + L di/dt + ∫i dt/C.

Это уравнение преобразуется в дифференциальное уравнение 2-го порядка, частным решением которого является выражение синусоидального тока i = I_m sin (ωt + ψ_i), для которого надо найти:

I_m и ψ_i или φ = ψ_u - ψ_i .

Если ток изменяется по гармоническому закону, то и напряжения на участках цепи изменяются по этому же закону. Тогда: U = U_q + U_L + U_c - из векторной диаграммы. Из ∆ ОВF: U² = (rI)² + (X_L - X_c )² I² и получаем:

Сопротивление цепи называется полным сопротивлением цепи. X = (X_L - X_c) называется реактивным сопротивлением цепи. Если в цепи преобладает индуктивное сопротивление, то Х положительно и φ > 0 и напряжение цепи опережает ток. Если в цепи преобладает емкостное сопротивление, то Х - отрицательно и φ < 0 и ток опережает напряжение. Следовательно, в подобных цепях φ может изменяться в пределах -π/2 < φ < π/2. Для комплексных действующих напряжений формула будет:

U = U_q + U_L + U_c = rI + j(X_L - X_c) I = Z I.

Законы Ома и Кирхгофа справедливы для мгновенных токов и напряжений, они справедливы и для комплексных напряжений и токов. Поэтому справедливо: I = U/Z.

Сумма комплексных токов в проводах, сходящихся в узле электрической цепи, равна нулю: I_к = 0.

Сумма комплексных ЭДС, действующих в замкнутом контуре, равна сумме комплексных падений напряжения в ветвях этого контура:

E_к = [r_к + j(X­_L - X_C)] I_к = Z_к I_к .

5. Электрическая цепь с параллельным соединением активного сопротивления R, индуктивности L и емкости С.

Рис. 13. Электрическая схема и векторные диаграммы напряжения и тока для электрической цепи с параллельным соединением R, L, C.

При u = U_m sin ωt общий ток по первому закону Кирхгофа будет:

i = i_q + i_L + i_c = (U_m/r) sin ωt + (U_m/ωL) sin (ωt - π/2) + ωCU_m sin (ωt + π/2).

Реактивный ток будет равен:

i_p = i_L + i_c = U_m[(1/ωL) - ωC] sin (ωt - π/2)

Если разделить стороны треугольника токов на векторной диаграмме на напряжение U, можно получить треугольник проводимостей и, учитывая соотношения для треугольника сопротивлений, получим:

cos φ = r/z; sin φ = x/z.

Соответственно токи и проводимости будут равны:

I_u = I cos φ = (U/z) (r/z) = (r/z²) U = g U;

I_p = I sin φ = (U/z) (x/z) = (x/z²) U = B U;

I = U/z = gU = √g² + B² U.

Лекция 6