
- •3 Задание
- •Числовое поле, аксиомы поля, поле комплексных чисел
- •Обратная матрица, определение существование, формула
- •Билет 3 Комплексные числа в алгебраическом виде, операции над ними.
- •Рангом матрицы а называется максиальное число линейно-независиых строк
- •Однородные системы линейных уравнений. Фундаментальная система решений. Система линейных уравнений называется однородной, если все свободные члены равны 0
- •Вопрос 3?
- •Матрицы и операции над ними
- •Универсальное определение кривых 2ого порядка
Матрицы и операции над ними
М атрица-
прямоугольная таблица чисел
атрица-
прямоугольная таблица чисел
А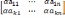 = Операции
над ними:
= Операции
над ними:
произведением матрицы А на число α αА называется матрица вида αА=
АКхN K – строк , N – столбцов А= (аij)KxN
Суммой матриц А= (аij) B=(bij) имеющих одинаковое число строк и столбцов называется матрица вида: А+В= (aij+bij)
П
 роизведение
матриц А= (аij)
и B=(bij)
Произведение строки А=( а1,…,аn)
на столбец В=
роизведение
матриц А= (аij)
и B=(bij)
Произведение строки А=( а1,…,аn)
на столбец В= 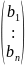 называется число
называется число
АВ= а1b1+a2b2+…+anbn Сума произведений соответствующих координат
Произведением 2х матриц есть произведение строк левой матрицы на столбцы правой
Пусть число столбцов матрицы А= (аij) равно числу строк матрицы B=(bij), тогда произведением матриц АВ=С
Называется
матрица С =(Сij)
в которой элемент (Сij),
стоящий на пересечении I
той строки и jтого
столбца равен произведению i-той
строки матрицы А на jтый
столбец матрицы В. Сij
= (ai1
….ain)
* =
ai1b1j+….+ainbnj
=
ai1b1j+….+ainbnj
 A1+a2+…+an=
A1+a2+…+an=
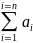
 = 1+
= 1+ (KxN)(NxP)=(KxP)
число столбцов левой N
= числу строк правой N
(2x5)(5x3)=(2x3)
Транспонирование- замена строк столбцами
и наоборот Ат
Свойства операций над матрицами:
(KxN)(NxP)=(KxP)
число столбцов левой N
= числу строк правой N
(2x5)(5x3)=(2x3)
Транспонирование- замена строк столбцами
и наоборот Ат
Свойства операций над матрицами:
1)αА=Аα 2) α(А+В)=αА+αВ 3)(α+β)А= αА+βА 4)А+В=В+А коммунтативность 5)(А+В)+С=А+(В+С) ассоциативность
6)(А*В)*С=А*(В*С)
7)A*(B+C)=AB+AC
8)(A+B)*C=AC+BC
транзитивность 9) существование 0 А+0=А
а) нулевая матрица: п умножению нейтральный
элемент
 б) нейтральный по сложению элемент
Матрица Е =
б) нейтральный по сложению элемент
Матрица Е =
10) Существует единичная матрица ЕкА=А; АЕn=А 11)(А+В)Т= ВТ+АТ 12) (АВ)Т=ВТАТ 13) А+(-1)А=0 14)квадратные матрицы матрица степени NxN
Теорема: Сумма произведений элементов какой либо строки(столбца) определителя на алгебраические дополнения к элементам другой строки(столбца) равна 0 ai1Аi1+ ainАin=0 (i≠j)
Теорема: Определитель произведения 2х квадратных матриц одинаковых степеней равен произведению их определителей. |AB|=|A|*|B|
Универсальное определение кривых 2ого порядка
Геометрическое место точек плоскости, отношение расстояний которых до данной точки, называемой фокусом, и до данной прямой, называемой директрисой, есть величина постоянная равная ε называется :
Эллипсом, если 0≤ε≤1 Параболой, если ε=1 гиперболой, если ε>1
Замечание: Каноническая теория кривых 2ого порядка Любая кривая 2ого порядка получается как сечение данного тела плоскостью
Окружность- перпендикулярно оси, гипербола- параллельно оси, парабола – параллельно образующей, эллипс – всё остальные
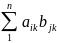
Билет 7 Скалярное произведение векторов, проекция одного вектора на другой. Понятие линейного пространства и подпространства, критерии подпространства
Скалярным произведением векторов а и b называется произведение модулей тих векторов на cos угла между ними а*b= |a|*|b|*cosγ γ=a^b
Углом между двумя векторами называется наименьший угол на который нужно повернуть один вектор до совмещения его с другим
Свойства скалярного произведения
A*b=b*a 2) (a+b)*c= a*c+b*c 3)αab=α(ab) 4) aa=a2≥0, a2 =0 a=0
Условие ортогональности векторов
Векторы ортогональны тогда и только тогда, когда их скалярное произведение равно 0 aперпендикулярна b ab=0=> |a||b|cosγ=0 =>|a|=0=> 0 перпендикулярен b; |b|=0=> перпендикулярен a; cosγ=0 => γ=π/2
Ab=(a1i+a2j+a3k)(b1i+b2j+b3k)=a1b1i2+a2b2j2+a3 b3 k2=a1b1 + a2b2+a3 b3
Ab=
a1b1
+
a2b2+a3
b3
(1) |a|= (2) Cosα=
(2) Cosα=
 =
=
 (3)
(3)
Проекцией
вектора а на направление вектора b
называется длина вектора а1
взятая со знаком «+» если его направление
совпадает с направлением b
и со знаком «-» в противном случаи.
Проекция а на b
равна =1) |a1|,
если а1 b1
2)
-|a1|,
если a1
b1
2)
-|a1|,
если a1 b1;
α<90=>
а1
b1
α>90=>
a1
b1;
Проекция a
на b
=
b1;
α<90=>
а1
b1
α>90=>
a1
b1;
Проекция a
на b
=
 (4) ; ab=
a*
(4) ; ab=
a* b=b*
b=b* a
(5)
a
(5)
Линейное пространство Линейным пространством V над полем F называется система элементов V с операциями сложения элементов и умножения элементов на числа из поля при этом должны выполняться следующие аксиомы линейного пространства.
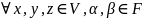 выполняется
: 1) сложение коммутативно х+у=у+х 2)сложение
ассоциативно(х+у)+z=x+(y+z)
выполняется
: 1) сложение коммутативно х+у=у+х 2)сложение
ассоциативно(х+у)+z=x+(y+z)
 4)
4)
 5)1*x=x
унитальность 6) α(βх)=(αβ)х дистрибутивность
5)1*x=x
унитальность 6) α(βх)=(αβ)х дистрибутивность
7) (α+β)х=αх+βх 8)α(х+у)= αх+αу Замкнутость относительно операций т.е. не выходим из V
Линейная зависимость и независимость элементов линейного пространства
Система элементов линейного пространства V а1…аn называется линейно зависимой, если существуют числа из поля F α1… αn не все равные 0, такие что α1а1+…+αnаn=0 нулевому элементу.
N≥2 Система элементов линейного пространства V а1…аn называется линейно зависимой тогда и только тогда когда хотя бы один из них линейно выражается через остальные.
В противно случаю система элементов а1…аn линейного пространства V линейно независима
Понятие подпространства и критерии его
Подмножества L линейного пространства V называется подпространством если оно является пространством относительно операций определённых на V/
Теорема1:
Критерий подпространства L
V
является подпространством тогда и
только тогда когда L
замкнута относительно операций сложения
и умножения на число. 1)
 2)
2)
 3) Если х
L
=>(-1)x
L=>x+(-1)x=0
L
Если выполняется 2 требования то L
является пространством
3) Если х
L
=>(-1)x
L=>x+(-1)x=0
L
Если выполняется 2 требования то L
является пространством
а1,…,аn л.з. 1) α1 ….αn не все =0 α1а1+…+αnan =0 2) n≥2 хотя бы один выражается через остальные
а1,…,аn л.н. 1) α1а1+…+αnan =0 α1….=αn=0 2) n≥2 ни один не выражается
Билет 8. Векторное произведение, его геометрический смысл, выражение через координаты. Базис и размерность линейного пространства.
Упорядоченная тройка некомпланарных векторов называется правой если из конца 3его вектора кратчайший поворот от 1ого ко 2оу виден против часовой стрелки в противно случаи тройка называется левой .
Векторное произведение векторов ab называется вектор с=AxB, удовлетворяющий условиям 1
С перпендикулярен А; С перпендикулярен B
|c|=|a||b| sin(a^b)
A,b,c – правая тройка
Модуль векторного произведения есть площадь параллелограмма построенного на сомножителях
Векторное произведение направлено как головка буравчика который мы вращаем от 1 множителя ко 2ому
Свойства:
АхВ= -ВхА – анти коммутативность
(А+В)хС=АхС+ВхС(αА)хВ=α(АхВ)
АхВ=
 =
i
=
i -j
-j +k
+k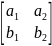 Условия
коллинеарности 2 вектора коллинарны
тогда и только тогда когда векторное
произведение их равно 0
Базис
и размерность линейного пространства
Условия
коллинеарности 2 вектора коллинарны
тогда и только тогда когда векторное
произведение их равно 0
Базис
и размерность линейного пространства
Базисом линейного пространства V называется система линейно независимых элементов, аксиальная по включению(при присоединении элемента л.н. исчезает)
Пусть е1…еn - ,базис V x V { е1…еn,x}- линейно зависимая
 α1…αn
,α
– не все равные 0, такие что αх+α1е1+…+αnen=0
α1…αn
,α
– не все равные 0, такие что αх+α1е1+…+αnen=0
α1е1+…+αnen=0 не все х1,…, αn =0 =>e1,…,en- л.з. – противоречие => α≠0
αx=
- α1e1-…-αnen
x=-
α1e1/α-…-αnen/α
 =
=
 =
= x=x1e1+…+xnen
(1)
x=x1e1+…+xnen
(1)
Выражение (1) называется разложением элемента х по базису е1….еn
Пусть система { е1….еn} – л.н. и для любого Х из V справедливо (1) тогда е1….еn образует базис. Х (X1,…, Xn)
Упорядоченная n кА чисел (X1,…, Xn) называется координатами элементов Х в базисе е1….еn
Множество упорядоченных n ок действительных чисел по компонентным сложениям и умножениям на действительное число образуют линейное пространство которое обозначается Rn .
Теорема: Пусть элементы b1…bs линейного пространства V есть линейные комбинации элементов a1….ak если s>k => то b1…bs – л.з.
b 1=α11a1+…+αk1ak
1=α11a1+…+αk1ak
b2=α12a1+…+αk2ak (2) Из коэффициентов равенства (2) составим матрицу: А=
bs=α1sa1+…+αksak
R(A)≤K K<S=> столбцы матрицы А линейно зависимы
β1…βs
не все =0 β1 +….βs
+….βs =
= (3)
(3)
β1b1=α11a1+α21a2+…+αk1ak
β2b2=α12a1+ α22a2+…+αk2ak
βSbS=α1Sa1+ α2Sa2+…+αkSak
Из равенства (3) следует что линейная комбинация β1b1+…+ βSbS=0а1+...+0ак=0 => b1,…,bS –л.з Линейная комбинация длины К линейно независимых может быть не больше чем К
Теорема 2: В любом базисе конечномерного линейного пространства V содержится одинаковое количество элементов
Е1,…,еn – базис V ; b1,…,bk- базис V ; k< n Поскольку е1= α11b1+α21b2+…+αk1bk en= α1nb1+α2nb2+…+αknbk => Е1,…,еn –л.з.
Противоречие => k≥n => k=n
Размерность конечномерного пространства V называется число элементов в базисе этого пространства
Теорема : разложение по базису единственно
(1’) X=X’1e1+…+X’nen = противное предположение
Х = Х1е1+…+Хnen
(1)-(1’) 0=(X1-X’1)e1+…+(Xn-X’n)en => X1=X’1 Xn=X’n чтд
Х(X1,…,Xn) Rn
Линейная оболочка элементов а1...ак
L(а1...ак) = {α1а1+…+αnan, α1….αn R}
Теорема : Линейная оболочка является пространством (подпространством )
L
V
L
– подпространство
1)
 2)
2)
 a=
α1а1+…+αkak
b=β1a1+…+βkak
a=
α1а1+…+αkak
b=β1a1+…+βkak
1)A+b= (α1+β1)a1+…+ (αk+βk)ak L
2)αa= αα1a1+…+ααkak L
Билет 9 Смешанное произведение его геометрический смысл, выражение через координаты . Линейный оператор и его матрица.
Смешанное произведение векторов называется число. Смешанное произведение некомпланарных векторов |abc| по модулю равно объему параллелепипеда построенного на сомножителях . Оно положительно если тройка |abc| правая и отрицательна если тройка левая
|abc |= Abc=(AxB)C= |AxB|*|C||Cos(AxB)^C)| |C||Cos(AxB)^C)|=H |AxB|= S параллелограмма SH=V параллелепипеда
У словие
компланарности : 3 вектора компланарны
тогда и только тогда когда их смешанное
произведение равно 0
словие
компланарности : 3 вектора компланарны
тогда и только тогда когда их смешанное
произведение равно 0
Abc = abc=bca=cab=-bac=-acb=-cba i-j-k=1
Координатами точки М называются координаты её радиус вектора ОМ
Уравнение соответствующим заданному множеству точек называется уравнение которому удовлетворяют координаты вех точек множества и не удовлетворяют координаты точек не принадлежащих множеству.
Множеством точек соответствующих заданному уравнению называются множества тех и только тех точек координаты которых удовлетворяют заданному уравнению.
Линейный оператор и его матрица.
Пусть V линейное пространство.
Определение1: преобразование линейного пространства V называется линейны оператором пространства V если выполняются следующие условия:
 1)
γ(x+y)=γ(x)+γ(y)
– аддитивность
1)
γ(x+y)=γ(x)+γ(y)
– аддитивность
2) γ(αх) =α(γх) – однородность
Γ(х) –образ элемента х под действием оператора γ
Если у=γ(х) – х называется прообраз у под действием оператора γ
П усть
(е) = (е1,…,еn)
– базис V,
тогда
усть
(е) = (е1,…,еn)
– базис V,
тогда 
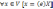

 X=
X= X=X1e1+…+Xnen
γ(x)=
γ(x1e1+…+xnen)
= γ(x1e1)
+…+γ(xnen)
= x1γ(e1)+…+xnγ(en)
γ(e1)-
образ элемента базиса
X=X1e1+…+Xnen
γ(x)=
γ(x1e1+…+xnen)
= γ(x1e1)
+…+γ(xnen)
= x1γ(e1)+…+xnγ(en)
γ(e1)-
образ элемента базиса
Как линейный оператор действует на элементы базиса
γ(е1)=
τ11е1+τ21е2+…+τn1en=
(e1…en)
 =e
=e
γ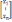
 (еn)=
τ1nе1+τ2nе2+…+τnnen=
(e1…en)
(еn)=
τ1nе1+τ2nе2+…+τnnen=
(e1…en)
 =e
=e
З амечание:
* =
=X1
амечание:
* =
=X1 +…+Xn
+…+Xn тогда матрицу умножают на столбец, как
будто берём линейную комбинацию столбцов
этой матрицы.
тогда матрицу умножают на столбец, как
будто берём линейную комбинацию столбцов
этой матрицы.
γ (х)=x1γ(e1)+…+xnγ(en)=(γ(е1)…γ(еn))
=(e
…(e)
=(e)(
…
)
=
(e)(X1
+…+Xn
)=
(e)*
(х)=x1γ(e1)+…+xnγ(en)=(γ(е1)…γ(еn))
=(e
…(e)
=(e)(
…
)
=
(e)(X1
+…+Xn
)=
(e)*
 Матрица
линейного оператора
Матрица
линейного оператора
Матрицей линейного оператора γ в базисе (е) [γ]e – обозначение. Называется матрица столбцы которой есть координаты образа элементов базиса в данном базисе. γ(х)=(е)[γ]eX (1)
P-
проекция на плоскость хОу [P]ijk
P(i)=i=(1,0,0)
P(j)=j=(0,1,0)
P(k)=k=(0,0,0)
[P]ijk= Матрица линейного оператора в базисе
I,j,k
Матрица линейного оператора в базисе
I,j,k
Операции над операторами:
1)(γ1+φ)(Х)= γХ+φХ
2)(αγ)(Х)=αγ(Х)
3)(γφ)(Х)=γ(φХ)
Заметим что между линейными операторами
1) [γ+φ]E=[γ] +[φ]E+[γ]E
2) [αγ]E= α[γ]E
3) [γφ]E=[γ]E[φ]E
Понятие
обратного оператора (γ)-1

 [γ-1]E=[γ]-1E
[γ-1]E=[γ]-1E
Структура общего решения неоднородной системы линейных уравнений
Общее решение неоднородной системы линейных уравнений равно сумме частного решения этой системы и общего решения соответствующее однородной системе.
Х1=Х0+α1С1+…+αn-rCn-r (9) Запись общего решения системы в геометрической форме Х – общее решение неоднородной системы, Х0 частное решение неоднородной системы; α1С1+…+αn-rCn-r – общее решение однородной системы Замечание: L – подпространство сдвигаем(гиперпространство, многообразие, сдвинутое подпространство)
Билет10 Различные уравнения плоскости, угол между плоскостями. Вид матрицы линейного оператора в базисе из собственных векторов.
1)Общее уравнение плоскости: Ax+By+Cz+D=0 вектор n=(A,B,C)≠0
2) Плоскость перпендикулярная вектору n=(A,B,C) и проходящая через точку M0=(X0,Y0,Z0): A(x-x0)+B(y-y0)+C(z-z0)=0
3) Плоскость проходящая через 3 данные точки М1=(X1,Y1,Z1), М2=(X2,Y2,Z2), М3=(X3,Y3,Z3), не лежащие на одной прямой:

4)Плоскость
отсекающая на осях координат ненулевые
отрезки a,b,c
описывается уравнением в отрезках:

5)Если
нормальные вектор единичный, и направлен
из начала координат в сторону плоскости,
то получаем нормальное
уравнение плоскости xcosα+ycosβ+
zcosγ-p=0
p≥0,
OPперпендикулярен
p,
ОР^Ox=α,
OP^Oy=β
OP^Oz=γ.
Для того чтобы общее уравнение привести
к нормальному виду, его нужно умножить
на μ= - нормирующий множитель, противоположен
D.Р
– расстояние плоскости от начала
координат, cos,sin
– направляющие вектора нормали
- нормирующий множитель, противоположен
D.Р
– расстояние плоскости от начала
координат, cos,sin
– направляющие вектора нормали
Отклонение точки М1=(X1,Y1,Z1) от плоскости L заданной нормальным уравнением, находится по формуле:
δ(M1,L)=x1cosα+y1cosβ+z1cosγ-p
Расстояние от точки М1=(X1,Y1,Z1) до плоскости L находится по формуле:
р(M1,L)
=|δ(M1,L)|=|
x1cosα+y1cosβ+z1cosγ-p|=
A=0 L||Ox B=0 L||Oy C=0 L||Oz D=0 L через начало координат
Вектор
А0,
направленный так же как и вектор А и
имеющий единичную длину называется
ортом вектора А А0=
Угол между плоскостями равен углу между их нормальными векторами
P1=A1x+B1y+C1z+D1=0
P2=A2x+B2y+C2z+D2=0
Cosα=
α=P1^P2
P1||P2

Условие
ортогональности: Р1
перпендикулярна
Р2
 =0
=0
Вид матрицы линейного оператора в базисе из собственных векторов
М
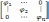 атрица
линейного оператора в базисе из
собственных векторов имеет диагональный
вид, причём на её диагонали стоят
собственные числа оператора.
атрица
линейного оператора в базисе из
собственных векторов имеет диагональный
вид, причём на её диагонали стоят
собственные числа оператора.
A= =>
[φ]E=диагон.
 Пусть [φ]E
имеет
диагональный вид
Пусть [φ]E
имеет
диагональный вид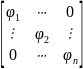
φ(ei)=(e)[φ]e =(e)
=(e)
 =(e1…en)
=(e1…en)
 =φ1e1
φ(ei)=
φiei
=φ1e1
φ(ei)=
φiei
ei – собственный элемент , φi – собственное значение
<= e1…en – Собственные тд. [φ]E=диагон.
[φ]E=
(φ(e1)
φ(e2)…
φ(en))=
φ(e1)=γ1e1
; φ(e2)=γ2e2
; φ(en)=γnen
=
 диагон.
γ1γ2γn-
собственные числа
диагон.
γ1γ2γn-
собственные числа
Билет 11. Различные уравнения прямой в пространстве. Матрица перехода к новому базису.
Общее уравнение прямой в пространстве:
A1x+B1y+C1z+D1=0 Чтобы плоскости не были параллельны N1=(A1,B1,C1) N2=(A2,B2,C2) N1xN2≠0
A2x+B2y+C2z+D2=0 (1)
N1xN2= =(
=( ,
,
 ,
,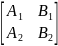 )
(
)2+(
)2+(
)2≠0
(2)
)
(
)2+(
)2+(
)2≠0
(2)
Система уравнений (1) с условием (2) задаёт прямую в пространстве такое задание называется общее уравнение прямой в пространстве
Теорема1: Всякая система уравнений (1) с условием (2) задаёт в пространстве прямую и наоборот. Любая прямая в пространстве может быть задана системой уравнений вида (1) с условием (2).
Каноническое
уравнение прямой в пространстве М0М||S
= S=(m,n,p)
– направляющий вектор
S=(m,n,p)
– направляющий вектор
Если одно или 2 из чисел m,n,p равны 0 это означает что соответствующий числитель равен 0
Параметрические уравнения прямой в пространстве
 t-
любое действительное число
t-
любое действительное число
X=mt+x0 Y=nt+y0 Z=pt+z0 (4)
M,n,p
– любого параллельного вектора
направляющего
Уравнения
прямой проходящей через 2 точки. S=M1M2

Угол
между прямой и плоскостью P:
Ax+By+Cz+D=0,то
N=(A,B,C)
S=(m,n,p)
sinα=|cosβ|
sinα= (6)
(6)
Условие
параллельности и перпендикулярности
L||p:Am+Bn+Cp=0
L
перпендикулярна p:
Точка пересечения прямой и плоскости P: Ax+By+Cz+D=0 L:
Для нахождения точек пересечения прямой L и плоскости р нужно:
Перейти к параметрическим уравнениям прямой вида (4) подставить полученные выражения для x,y,z, в уравнения плоскости р и найти параметр t , тогда если t = t0 то точка пересечения прямой и плоскости К имеет координаты К(mt+x0, nt+y0, pt+z0)
Расстояние от точки до прямой в пространстве. Площадь параллелограмма =|S|d=|M0M1*S|
d= (7)
(7)
Расстояние от точки до прямой в пространстве
Формулы деления отрезка в данном соотношении
γ= Найти координаты точки М М1М=γММ2
Найти координаты точки М М1М=γММ2
( )=γ(х2
–x;
y2-y;
z2-z)
)=γ(х2
–x;
y2-y;
z2-z)
x-x1=
γ(х2
–x)
x-x1=
γх2
–γx
=> X= (8) Замечание 1)γ≠-1
(8) Замечание 1)γ≠-1
2)Если точка М вне отрезка, то γ<0 3)От 1ой точки до делящей, к длине отрезка, от делящей до 2ой
Матрица перехода к новому базису (e)=(e1…en) - старый
(e’)=(e’1…e’n)- новый e1=α11e’1+ α21e’2+…+ αn1e’n
e2= α12e’1+ α22e’2+…+ αn2e’n (1)
en= α1ne’1+ α2ne’2+…+ αnne’n
Система
(1) в матричной форме: (e1…en)=(e’1…e’n)*S
S= (e)=
(e’)S
(e’)=(e)T=(e’)S
*T
S*T=E
(e)=
(e’)S
(e’)=(e)T=(e’)S
*T
S*T=E
Матрица перехода от старого (е) базиса к новому (e’) называется матрица, столбцы которой, есть координаты элементов старого базиса в новом.
Матрица перехода обратима при этом S-1 является матрицей перехода от базиса (e’) к базису (е). Координаты вектора и матрица линейного оператора зависят от базиса.
Билет 12 Различные уравнения прямой на плоскости, геометрический смысл параметров. Формула преобразования координат вектора при переходе к новому базису
1)Прямая
на плоскости хОу Р хОу: z=0
P=Ax+By+Cz+D=0
если в хОу, то С=0
Р хОу: z=0
P=Ax+By+Cz+D=0
если в хОу, то С=0
P=Ax+By+C =0 (1)
Теорема 1. Всякая прямая на плоскости может быть задана уравнениями вида (1) и наоборот, всякое уравнение вида (1) задаёт прямую на плоскости, поэтому уравнение вида (1) является общим уравнением плоскости. N=(A,B,C) перпендикулярно Р n=(A,B) перпендикулярно L L: Ax+By+C=0 S=(-B,A) nS=(A,B)(-B,A)=-BA+BA=0 nперпендикулярно S
Из общего уравнения (1) можно найти:
Вектор нормали к прямой n=(A,B)
Направляющие S=(-B,A)
Угол наклона прямой – угол, лежащий в верхней полуплоскости и образованный прямой с положительным направление оси Ох (α)
Угловым коэффициентом прямой называется тангенс угла наклона, относится к прямым не параллельным оси Оу
Углом между двумя прямыми, называется угол, на который нужно повернуть 1ую прямую , против часовой стрелки до совмещения её со 2ой прямой
Вектор нормали прямой называется вектор перпендикулярный прямой
Направляющий вектор параллелен прямой
Ax+By+Cz+D=0 (1) n=(A,B) S=(-B,A)
Виды уравнений прямой на плоскости
Название |
Вид уравнения |
Геометрический смысл параметра |
Общее |
Ax+By+Cz+D=0 |
N=(A,B) перпендикулн L S=(-B,A) ||L |
Уравнение прямой с угловым коэффициентом |
Y=kx+b |
K=tgα- угл. Коэфф. B- отрезок на оси Oy |
Ур.пр. проходящей через данную точку в данном направлении |
y-y0=k(x-x0) |
M1(x1,y1) L k- угловой коэффициент |
Ур. Пр. проходящей через 2 данные (.) |
|
M1(x1,y1) L М2(х2,у2) L |
Ур.Пр. в отрезках на осях |
|
а – отрезок на оси Ох , b- отр.на оси Оу |
Нормальное уравнение |
Xcosα+ysinα-p=0 |
n=(cosα,sin |
Уравнение прямой || оси Оу |
х=а |
а- отрезок на оси Ох |
2)Х=х1е1+…+хnen=(e)x x=(e)X=(e’)SX (e’)X’=(e’)SX SX=X’(2) [φ]e’=S[φ]eS-1 (3)
SX=X’(2) - Формула преобразования координат вектора при переходе к новому базису
φ(х)=(е)[φ]eX=(e’)S[φ]eX=(e’)S[φ]eS-1X’ φ(х)=(e’)S[φ]eS-1X’ X’=SX=>X=S-1X’
(e’)[φ]eX-1=(e’)S[φ]eS-1X’ [φ]eX’=S[φ]eS-1X’ =>X’([φ]e’ -S[φ]eS-1)=0=> X’- любой вектор, матрица нулевая=> [φ]e’ -S[φ]eS-1=0=> [φ]e’ =S[φ]eS-1 (3)
Формулы преобразования вектора и матрицы линейного оператора при переходе к новому базису.
Билет 13 Угол между 2 мя прямыми , условия параллельности и перпендикулярности. Преобразование линейного оператора при переходе к новому базису
Название |
Вид формулы |
Геометрич. Смысл параметра |
Угол между 2мя прямыми А) у=к1х+b1 Y=к2х+b2 Б) A1x+B1y+C1=0 A2x+B2y+C2=0 |
Tgφ=
Cosφ= |
K1, k2- угловой коэффициент
n1=(A1,B1) n2=(A2,B2)
|
Условия || |
А) k1=k2 Б)
|
|
Условие перпендикулярности |
Б) A1A2+B1B2=0 |
|
Расстояние от (.) до прямой на плоскости |
d= |
M0(x0,y0) данная(.) Ax+By+C=0 уравнение плоскости |
Угловой коэффициент |
K=
|
M1(x1,y1) L M2(x2,y2) L |
φ(х)=(е)[φ]eX=(e’)S[φ]eX=(e’)S[φ]eS-1X’ φ(х)=(e’)S[φ]eS-1X’ X’=SX=>X=S-1X’
(e’)[φ]eX-1=(e’)S[φ]eS-1X’ [φ]eX’=S[φ]eS-1X’ =>X’([φ]e’ -S[φ]eS-1)=0=> X’- любой вектор, матрица нулевая=> [φ]e’ -S[φ]eS-1=0=> [φ]e’ =S[φ]eS-1 (3)
Формулы преобразования вектора и матрицы линейного оператора при переходе к новому базису.
Билет14Эллипс определение, каноническое уравнение чертёж
Решение неоднородной системы линейных уравнений методом гаусса
Эллипс геометрическое место точек плоскости сумма, расстояний которых до 2х данных точек, называемых фокусами, есть величина постоянная равная 2а
М1F2+MF1=2a
 +
+ =2a
=2a
 =
= (x+c)2+y2=4a2-4a
(x+c)2+y2=4a2-4a +(x-c)2+y2
+(x-c)2+y2
X2+2xc+c2=4a2-4a
+x2-2xc+c2
4xc-4a2=-4a
(xc-a2)2=a2 (cx-a2)2=a2(x2-2cx+c2+y2)
(cx-a2)2=a2(x2-2cx+c2+y2)
C2x2-2a2cx+a4=a2x2-2a2cx+a2c2+a2y2 (a2-c2)x2+a2y2=a4-a2c2 (a2-c2)x2+a2y2=a2(a2-c2) (a2-c2)>0
A2-c2=b2 обозначим b2x2+a2y2=a2b2\:a2b2
 =1
– каноническое уравнение эллипса
=1
– каноническое уравнение эллипса
А1,А2; В1, В2 – вершины эллипса
F1,F2 – фокусы эллипса А1А2=2а
А- большая полуось, b – малая полуось с- половина фокусного расстояния а2=b2+c2 связь между параметрами эллипса
Число
ε= =>эксцентриситет эллипса, служит мерой
сплющенности эллипса, чем больше ε , те
больше сплющен эллипс. Чем больше с те
больше сплющен эллипс, с=0 – окружность
0<ε<1 c<a
– для эллипса ε
[0;1]
=>эксцентриситет эллипса, служит мерой
сплющенности эллипса, чем больше ε , те
больше сплющен эллипс. Чем больше с те
больше сплющен эллипс, с=0 – окружность
0<ε<1 c<a
– для эллипса ε
[0;1]
Прямые
параллельные оси Оу и имеющие уравнения
Х=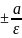 – называется директрисами эллипса
– называется директрисами эллипса
Расстояние
от точки эллипса до фокуса называется
фокальным радиусом эллипса
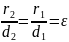 r1=a+εx
r2=a-εx
r1=a+εx
r2=a-εx
Окружность является частным случаем эллипса
Если
(.) F1
и F2
совпадают, т.е. с=0 то эллипс становится
окружностью.
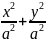 =1
х2+у2=а2
Фокальные свойства Эллипса???
=1
х2+у2=а2
Фокальные свойства Эллипса???
Решение неоднородной системы линейных уравнений методом Гаусса
А11х11+…+а1nx1n=b1
Ak1x1+…+aknxkn=bk (1) – система
2 системы линейных уравнений называются эквивалентными, если множество их решений совпадает.
А= расширенная матрица системы однозначно
определяет систему
расширенная матрица системы однозначно
определяет систему
Элементарные преобразования строк расширенной матрицы системы (1). Переводят систему (1) в эквивалентную
Приведём расширенную матрицу к ступенчатому виду, элементарными преобразованиями строк
А А’=
А’= (2)
(2)
Система (1) совместна, тогда и только тогда, когда в ступенчатом виде (2) b’r+1 =0
0x1+…0xn=br+1 Система не совместна. Если при приведении расширенной матрицы к ступенчатому виду образуется строка b’r+1 ≠0, то система не совместна.
r=n
r<n
Если r=n, то А’= (3) Считаем с конца строки
A’nnxn=b’n

a’n-1,n-1xn-1+a’n-1,nxn=b’n-1 xn-1=…
r<n Система имеет бесконечное множество решений. Поэтому есть общее решение и частное.
Параметрическая форма записи общего решения – это такая форма, в которой неизвестные x1…xn, выражаются как линейные функции некоторых параметров, принимающих произвольные значения
А’= (4) Нулевые строки отбрасываем, ведь 0=0
(4) Нулевые строки отбрасываем, ведь 0=0
Алгоритм:
Неизвестные попавшие в углы ступенек называются базисными
Все остальные свободные
Переносим свободные неизвестные в правую часть и выражаем базисные неизвестные через свободные, эти выражения и есть общее решение системы в параметрической форме , роль параметров играют свободные переменные .
Пример1:
 1)
x1,x3,x4
– базисные х2,х5-
свободные
1)
x1,x3,x4
– базисные х2,х5-
свободные
Обратным ходом алгоритма Гаусса получим в столбцах базисных переменных единичную матрицу
 Переписать строки расширенной матрицы
на языке уравнений
Переписать строки расширенной матрицы
на языке уравнений
X1+4x2+ x5=
x5=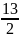
X3- x5=
X4+2x5=3
4)Выразить базисные неизвестные через свободные
X1=-4x2-
x5 Общее решение в параметрической форме
Общее решение в параметрической форме
X3= x5-
X4=-2x5+3
Замечание: (5) является общим решением в том смысле, что после подстановки выражений (5) в исходную систему все уравнения превращаются в тождества
Придавая свободным переменным х2 и х5 произвольные значения получаем частные решения системы
Если в системе есть хоть 1 свободная переменная, она имеет бесконечно много решений, поэтому по числу решений системы классифицируются следующим образом:
Число решений 0 система несовместна
Число решений 1 система определенная
Число решений ∞ система совестная неопределенная
Совестные r(A)=r(A) – Определённая r=n неопределенная r<n
Несовместная
r(A)≠r( )
)
Билет15. Гипербола, определение, асимптоты, каноническое уравнение, чертёж. Собственные векторы и собственные значения линейного оператора.
Гипербола- геометрическое место точек плоскости разность расстояний которых до 2х данных точек называемых фокусами есть вличина постоянная равная 2а
1)Прямая не ограниченная
|MF1-MF2|=2a
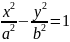 c2=a2+b2
Связь между параметрами гипарболы
c2=a2+b2
Связь между параметрами гипарболы
А1А2 – вершины гиперболы, F1F2 – фокусы
a<c y=+- bi при х=0
а- действительная ось, b - мнимая ось, с – половина фокусного расстояния
Число ε = называется эксцентриситетом гиперболы ε>1
Прямые параллельные оси Оу и имеющие уравнение называются директрисами гиперболы
Х=
 Левая ветвь r1-εx-a
r2-εx+a
Левая ветвь r1-εx-a
r2-εx+a
Правая ветвь r1=εx+a r2=εx-a
Прямые
с уравнениями у= x
называются асимптотами гиперболы
x
называются асимптотами гиперболы
Фокальные свойства выходит будто его выпустили из другого фокуса
a=b на 45 градусов
Если гипербола равнобочная т.е. а=b , то повернутая на 45 градусов она превращается в «школьную»
Собственные элементы и собственные значения линейного оператора
Ненулевой элемент Х линейного пространства V называется собственным элементом линейного оператора [φ] если для него выполняется равенство φ(х)=γх (1) х≠0 V при этом γ называется собственным значением(числом) линейного оператора φ соответствующим элементу Х
γх=γ’х =>(γ-γ’)x=0=> γ=γ’
Собственный элемент под действием оператора меняется самым простейшим методом( может только растянуться)
Как равенство (1) выглядит на языке матриц
Фиксируем (е) => [φ]e= A
Φ(x)=(e)[φ]ex γx=(e)γx
AX=γX (1’)
AX-γEX=0 X≠0 (A-γE)X=0 (2) Однородная система линейных уравнений с матрицей A-γE
|A-γE| =0 Чтобы система 2 имела ненулевое решение необходимо и достаточно чтобы
|A-γE|
=
 =γЕ=
=γЕ= =
)(
=
)( -а21а12=γ2-γ(а11+а22)+а11а22-а21а12
-а21а12=γ2-γ(а11+а22)+а11а22-а21а12
Билет 16.Парабола определение, каноническое уравнение, чертёж.
Парабола- геометрическое место точек равноудалённых от данной точки, называемой фокусом и от данной прямой, называемой директрисой.
Р- параметр параболы, расстояние от фокуса до директрисы MF=MK
 =
=

 -
каноническое уравнение параболы
-
каноническое уравнение параболы
 -
эксцентриситет r=x+
-
эксцентриситет r=x+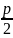 Фокальные свойства параболы: луч идёт
параллельно оси, симметрии параболы.
Собираются в одной точке.
Фокальные свойства параболы: луч идёт
параллельно оси, симметрии параболы.
Собираются в одной точке.
Собственные векторы линейного оператора, относящиеся к разным собственным значениям.
 (1)
х≠0
V
γ- называется собственным значением(числом)
линейного оператора φ соответствующим
элементу Х
(1)
х≠0
V
γ- называется собственным значением(числом)
линейного оператора φ соответствующим
элементу Х
γх=γ’х =>(γ-γ’)x=0=> γ=γ’
Собственный элемент под действием оператора меняется самым простейшим методом( может только растянуться)
Как равенство (1) выглядит на языке матриц
Фиксируем (е) => [φ]e= A
Φ(x)=(e)[φ]ex γx=(e)γx
AX=γX (1’)
AX-γEX=0 X≠0 (A-γE)X=0 (2) Однородная система линейных уравнений с матрицей A-γE
|A-γE| =0 Чтобы система 2 имела ненулевое решение необходимо и достаточно чтобы
|A-γE| = =γЕ= = )( -а21а12=γ2-γ(а11+а22)+а11а22-а21а12
Билет 17 Линейное пространство, подпространство, линейная оболочк\
Линейным пространством V над полем F называется система элементов V с операциями сложения элементов и умножения элементов на числа из поля при этом должны выполняться следующие аксиомы линейного пространства.
Подмножества L линейного пространства V называется подпространством если оно является пространством относительно операций определённых на V.
Линейная оболочка элементов а1...ак
L(а1...ак) = {α1а1+…+αnan, α1….αn R}
Теорема : Линейная оболочка является пространством (подпространством )
L V L – подпространство 1) 2) a= α1а1+…+αkak b=β1a1+…+βkak
1)A+b= (α1+β1)a1+…+ (αk+βk)ak L
2)αa= αα1a1+…+ααkak L
Привидение уравнения линий второго порядка к каноническому виду
Эллипс геометрическое место точек плоскости сумма, расстояний которых до 2х данных точек, называемых фокусами, есть величина постоянная равная 2а
М1F2+MF1=2a
+ =2a = (x+c)2+y2=4a2-4a +(x-c)2+y2
X2+2xc+c2=4a2-4a +x2-2xc+c2 4xc-4a2=-4a (xc-a2)2=a2 (cx-a2)2=a2(x2-2cx+c2+y2)
C2x2-2a2cx+a4=a2x2-2a2cx+a2c2+a2y2 (a2-c2)x2+a2y2=a4-a2c2 (a2-c2)x2+a2y2=a2(a2-c2) (a2-c2)>0
A2-c2=b2 обозначим b2x2+a2y2=a2b2\:a2b2
=1 – каноническое уравнение эллипса
Гипербола- геометрическое место точек плоскости разность расстояний которых до 2х данных точек называемых фокусами есть вличина постоянная равная 2а
1)Прямая не ограниченная |MF1-MF2|=2a
Парабола- геометрическое место точек равноудалённых от данной точки, называемой фокусом и от данной прямой, называемой директрисой.
Р- параметр параболы, расстояние от фокуса до директрисы MF=MK
= - каноническое уравнение параболы
Билет18 Векторы линейные операции над ними, симметрические матрицы и их характеристические числа и собственные векторы.
Вектором называется направленный отрезок прямой, векторы в аналитической геометрии рассматриваются с точностью до параллельного переноса. ( мы не фиксируем начало вектора)
Длиной вектора или его модулем называется расстояние между началом и концом вектора. Если это расстояние равно нулю, то вектор называется нулевым или обозначается 0. Направление – произвольное
Векторы, расположенные на параллельных прямых – коллинеарные
Векторы расположенные на прямых параллельных одной и той же плоскости, называются компланарными.
2 вектора всегда компланарны
Суммой двух векторов является вектор для нахождения которого можно пользоваться двумя правилами: правилом параллелограмма и правилом треугольника.
Правило параллелограмма: суммой векторов а и b приложенных к одной точке, называется вектор, совпадающий с диагональю параллелограмма, построенного на векторах а и b.
Правило треугольника: Если начало вектора b совещается с концом вектора а, то суммой векторов а и b называется вектор, направленный из начала вектора а в конец вектора b.
Разностью векторов а и b называется вектор с, равный сумме вектора а и вектора, противоположного b.
Произведением
вектора а на действительное число γ
называется вектор b=γa,
такой что 1)|b|=|γ||a|,
2)b
a,
если γ>0, и b
a,
если γ<0 Из этого определения следует,
что а||b

Вектором а0 называется ортом вектора а, если |a0|=1 и а0 а. Вектор, длина которого равна 1, называется единичным вектором или просто ортом.
Симметрические матрицы и их характеристические числа и собственные векторы.
?????????????????????????????????????
Билет 19Декартовы прямоугольные координаты на плоскости и в пространстве
Декартовой системой координат на плоскости( в пространстве) называется совокупность точки( начала координат) и ортонормированного базиса. а=а1i+a2j+a3k=(a1, a2, a3)=a |i|=|j|=1 I перпендикулярна j. В пространстве V3 геометрических векторов рассмотрим различные базисы {e1,e2,e3} такие что e1,e2,e3 попарно перпендикулярны и |e1|=|e2|=|e3|=1 Такие базисы называются ортонормированными. Некоторые из них похожи на другие т.е. совмещаются при подходящих поворотах. Если брать только непохожие базисы то останется только два, буде говорить класса ориентации. Правый ортонормированный базис в V3 называется декартовым прямоугольным базисом. Обозначается такой базис {I,j,k}. Совокупность точки О (начала координат) и базиса {I,j,k}называется прямоугольной декартовой системой координат. Проекцией Прba вектора а на вектор b называется длина вектора b’ взятая со знаком +, если b b’ и со знаком минус, если b b’. Координаты вектора а в декартовой прямоугольном базисе являются проекциями а на координатные оси:
а=xi+yj+zk x=прia ; y= прja z= прka
Если
α,β,γ – углы, которые вектор а составляет
с векторами I,j,k,
то x=|a|cosα
y=|a|cosβ
z=|a|cosγ
a0=(cosα,cosβ,cosγ)= (x,y,z)
(x,y,z)
Величины
cosα,cosβ,cosγ
называются направляющими косинусами
вектора а и связаны соотношением: соз2α+
соз2β+соз2γ=1.
Длина вектора а находится по формуле
|a|= .
Вектор ОМ= xi+yj+zk
называется радиус-вектором точки
М(x,y,z).
Если М1(х1,у1z1)
и М2(х2,у2,z2)
- две точки в прямоугольной декартовой
системе координат, то вектор М1М2
имеет координаты (x2-x1,y2-y1,z2-z1).
Пусть А(х1,у1z1)
и В(х2,у2,z2)-
две точки в прямоугольной декартовой
системе координат, а точка М делит
отрезок АВ в отношении
.
Вектор ОМ= xi+yj+zk
называется радиус-вектором точки
М(x,y,z).
Если М1(х1,у1z1)
и М2(х2,у2,z2)
- две точки в прямоугольной декартовой
системе координат, то вектор М1М2
имеет координаты (x2-x1,y2-y1,z2-z1).
Пусть А(х1,у1z1)
и В(х2,у2,z2)-
две точки в прямоугольной декартовой
системе координат, а точка М делит
отрезок АВ в отношении
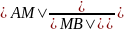 =γ.
Координаты точки М находятся по следующи
формулам деления отрезка в дано
соотношении:
=γ.
Координаты точки М находятся по следующи
формулам деления отрезка в дано
соотношении:
Хм= ум=
ум=
 zM=
zM= .
Пусть а=(х1,у1z1)
и b=(х2,у2,z2)-векторы
в прямоугольной декартовой системе
координат. Тогда
.
Пусть а=(х1,у1z1)
и b=(х2,у2,z2)-векторы
в прямоугольной декартовой системе
координат. Тогда
а=b
x1=x2;y1=y2;z1=z2;
a||b
 c=a+b
c=(x2+x1,y2+y1,z2+z1)
b=γa
b=(γх1,
γу1,γz1)
c=a+b
c=(x2+x1,y2+y1,z2+z1)
b=γa
b=(γх1,
γу1,γz1)
Структура общего решения неоднородной системы линейных уравнений
Общее решение неоднородной системы линейных уравнений равно сумме частного решения этой системы и общего решения соответствующее однородной системе.
Х1=Х0+α1С1+…+αn-rCn-r (9) Запись общего решения системы в геометрической форме Х – общее решение неоднородной системы, Х0 частное решение неоднородной системы; α1С1+…+αn-rCn-r – общее решение однородной системы Замечание: L – подпространство сдвигаем(гиперпространство, многообразие, сдвинутое подпространство) Билет 20 Критерий компланарности 3 векторов
Условие компланарности : 3 вектора компланарны тогда и только тогда когда их смешанное произведение равно 0
Базис пространства решений однородной системы линейных уравнений.
Определение : Фундаментальной системой решений(ФСР) однородной системы линейных уравнений (1) называется базис пространства решений этой системы . Пусть ФСР = {C1…Ck} x L [x=α1C1+…+αkCk] (2)
(2)называется векторной формой записи общего решения однородной системы (1)
Нахождение ФСР 1)x1,…,xr – базисные хк+1,..,хn – свободные
2) Выражение базисных элементов через свободные
Х1= а1r+1xr+1 +…+ a1nxn
X2 = а2r+1xr+1 +…+ a2nxn (3)
Xr= = аrr+1xr+1 +…+ arnxn
Найдём общее решение в параметрической форме. Чтобы найти векторы С1,…, Ск (ФСР) придадим свободным неизвестным Хr+1,...,Xn линейно независимые наборы значений (n-r).
Хr+1,...,Xn Придадим свободным неизвестным и для каждого набора найдём частное решение r- базисных, n-r - неизвестных
С1= C2 = Cn-r= (4) X1= a1r+1Xr+1a1r+2Xr+2+…+a1nXn
Любое решение системы (1) линейно выражается через C1 , Cn X0= предположим, что этот набор решений системы (1). Стало быть его компоненты удовлетворяют системе (2) равенств
а1r+1X0r+1+…+a1nX0n (5) Из (5) Следует что = X0r+1 +…+X0n (6)
X02= а2r+1X0r+1+…+a2nX0n
X0r= аrr+1X0r+1+…+arnX0n
Из последнего (6) выражение следует что вектор
Х= = X0 r+1 +…+X0n X = X0r+1C1 +…+ X0nCn-r (7) мы получили что произвольные решения действительно равняются линейной комбинации ФСР. Векторы C1 … Cn-r образуют базис пространства решения
Размерность пространства решений однородной системы уравнений n-r где n –число неизвестных r - ранг матрицы системы
Билет 21 Квадратичные формы, преобразование матрицы квадратичной формы при переходе к новому базису.
Квадратичной формой n переменных x1….xn называется однородным многочлен второй степени относительно этих переменных:
Ф(x1….xn)
= а11х12+a12x1x2+…+a1nx1xn+a21x2x1+a22x22+…+annxn2,
(1) или в матричном виде Ф(x1….xn)=
ХТАХ,
где Х= ,
А=(аij)NxN.
,
А=(аij)NxN.
Квадратичная форма – функция, ставящая в соответствие каждому элементу х евклидова пространства Еn некоторое вещественное число Ф(х). Тогда Ф в (1) есть не что иное как функция от координат вектора х.
Матрица А, называемая матрицей квадратичной формы Ф, всегда симметрична, поскольку мы всегда можем потребовать, чтобы аij= аji,так как это коэффициенты при равных произведениях хixj и xjxi.
По
сколько в (1) используются координаты
вектора, то эта запись зависит от
выбранного базиса, и, следовательно, от
базиса зависит также и матрица квадратичной
формы. Пусть ε и ε’ – два базиса Еn,
А- матрица квадратичной формы Ф в базисе
ε, а А’ - в базисе ε’. Тогда А’= A
A (2)
(2)
Две квадратичные формы называются эквивалентными, если одна из них переводятся в другую посредством невырожденного линейного преобразования координат. Поскольку при невырожденном линейном преобразовании базис переходит в базис, матрицы двух эквивалентных квадратичных форм будут связаны соотношением вида (2).
Каноническим видом квадратичной формы называется эквивалентная ей квадратичная форма, содержащая только квадраты переменных:
Ф’(x1….xn)=
γ1x12+…+γnxn2=XTBX
, B= .
Матрица квадратичной формы в каноническом
виде диагональна. Базис, в котором
квадратичная матрица принимает
канонический вид, называется каноническим.
.
Матрица квадратичной формы в каноническом
виде диагональна. Базис, в котором
квадратичная матрица принимает
канонический вид, называется каноническим.
Прямая в пространстве, переход от общих уравнений к каноническим.
Общее уравнение прямой в пространстве:
A1x+B1y+C1z+D1=0 Чтобы плоскости не были параллельны N1=(A1,B1,C1) N2=(A2,B2,C2) N1xN2≠0
A2x+B2y+C2z+D2=0 (1)
N1xN2= =( , , ) ( )2+( )2+( )2≠0 (2)
Система уравнений (1) с условием (2) задаёт прямую в пространстве такое задание называется общее уравнение прямой в пространстве
Теорема1: Всякая система уравнений (1) с условием (2) задаёт в пространстве прямую и наоборот. Любая прямая в пространстве может быть задана системой уравнений вида (1) с условием (2).
Каноническое уравнение прямой в пространстве М0М||S = S=(m,n,p) – направляющий вектор
Если одно или 2 из чисел m,n,p равны 0 это означает что соответствующий числитель равен 0
Параметрические уравнения прямой в пространстве
t- любое действительное число
X=mt+x0 Y=nt+y0 Z=pt+z0 (4)
M,n,p – любого параллельного вектора направляющего Уравнения прямой проходящей через 2 точки. S=M1M2
Угол между прямой и плоскостью P: Ax+By+Cz+D=0,то N=(A,B,C) S=(m,n,p) sinα=|cosβ| sinα= (6)
Условие параллельности и перпендикулярности L||p:Am+Bn+Cp=0 L перпендикулярна p:
Точка пересечения прямой и плоскости P: Ax+By+Cz+D=0 L:
Для нахождения точек пересечения прямой L и плоскости р нужно:
Перейти к параметрическим уравнениям прямой вида (4) подставить полученные выражения для x,y,z, в уравнения плоскости р и найти параметр t , тогда если t = t0 то точка пересечения прямой и плоскости К имеет координаты К(mt+x0, nt+y0, pt+z0)
Расстояние от точки до прямой в пространстве. Площадь параллелограмма =|S|d=|M0M1*S|
d= (7)
Расстояние от точки до прямой в пространстве
Формулы деления отрезка в данном соотношении
γ= Найти координаты точки М М1М=γММ2
( )=γ(х2 –x; y2-y; z2-z)
x-x1= γ(х2 –x) x-x1= γх2 –γx => X= (8) Замечание 1)γ≠-1
2)Если точка М вне отрезка, то γ<0 3)От 1ой точки до делящей, к длине отрезка, от делящей до 2ой
Билет 22Понятие евклидова пространства, неравенство Коши-Буняковского. Теорема Кронекера Капелли.
Вещественное линейное пространство называется евклидовым, если в нём каждой паре векторов х,у поставлено в соответствие число (х,у) , называемое скалярным произведением векторов х и у, для которого выполняются следующие условия:
(х,у) = (у,х)
(х1+х2,у) = (х1,у)+(х2,у)
(γх,у)= γ(х,у)
(х,х)≥0, причем (х,х) =0 х=0
Аксиомы евклидова пространства:
Нормой в линейном пространстве L называется функция, ставящая в соответствие каждому вектору х L вещественное число ||x|| , для которого выполняются следующие условия:
||x||>0 , если х≠0, и ||0||=0
||γx||=|γ| ||x||, γ R
 x,
y
L
(||x+y||≤||x||+||y||)
Неравенство треугольника
x,
y
L
(||x+y||≤||x||+||y||)
Неравенство треугольника
В
евклидовом пространстве Е норму можно
задать следующим образом: ||x||=
Неравенство
Коши Буняковского
 Е
(|(x,y)|≤||x||
||y||)
Такая норма носит называние евклидовой.
Е
(|(x,y)|≤||x||
||y||)
Такая норма носит называние евклидовой.
Углом
между векторами х и у называется угол
φ
[0,π] косинус которого вычисляется по
формуле cosφ=
Векторы х и у называются ортогональными, если (х,у) =0. Система векторов x1….xn называется ортогональной, если векторы этой системы попарно ортогональны друг другу.
Теорема Кронекера Капелли
Система 1 совместна тогда и только тогда когда ранг матрицы системы равен рангу расширенной матрицы. (1) совместна r(A)=r(Ā)
=> (1) совместна т д ч r(A)=r(Ā) Существуют α₁αn – решения (1)
Система 2:
А1 = Аn = B= тогда 2 означает α₁А1 + …+ αn An =B (2’ )=> Столбцы А1, Аn, В – линейно зависимы
Ранг столбцов r(А1, …,An) = r(А1, …,An ,B)
Потому что В через них линейно выражается
r(A)=r(Ā)
<= r(A)=r(Ā) т д что (1) совместна , В линейно зависимый со столбцами А1, …,An
r(A)=r(Ā) => B линейно выражается через А1, …,An => α₁А1 + …+ αn An =B выполняется равенство (2’), а (2’) означает, чо выполняется равенство (2), => а из равенства (2) следует что система (1) совместна
Билет 23 Существование ортогонального базиса в евклидовом пространстве.
Нормой в линейном пространстве L называется функция, ставящая в соответствие каждому вектору х L вещественное число ||x|| , для которого выполняются следующие условия:
||x||>0 , если х≠0, и ||0||=0
||γx||=|γ| ||x||, γ R
x, y L (||x+y||≤||x||+||y||) Неравенство треугольника
В евклидовом пространстве Е норму можно задать следующим образом: ||x||=
Неравенство Коши Буняковского Е (|(x,y)|≤||x|| ||y||) Такая норма носит называние евклидовой.
Углом между векторами х и у называется угол φ [0,π] косинус которого вычисляется по формуле cosφ=
Векторы х и у называются ортогональными, если (х,у) =0. Система векторов x1….xn называется ортогональной, если векторы этой системы попарно ортогональны друг другу.
Расстояние от точки до прямой в пространстве.
Расстояние от точки до прямой в пространстве. Площадь параллелограмма =|S|d=|M0M1*S|
d= (7)
Расстояние от точки до прямой в пространстве
Формулы деления отрезка в данном соотношении
γ= Найти координаты точки М М1М=γММ2
( )=γ(х2 –x; y2-y; z2-z)
x-x1= γ(х2 –x) x-x1= γх2 –γx => X= (8) Замечание 1)γ≠-1
2)Если точка М вне отрезка, то γ<0 3)От 1ой точки до делящей, к длине отрезка, от делящей до 2ой
Билет 24 Приведение квадратичной формы к каноническому виду с помощью ортогональных преобразований.
Пусть
А матрица квадратичной формы в старом
ортонормированном базисе ε. Нам необходимо
подобрать такую смену базиса чтобы в
новом базисе ε’ матриа квадратичной
формы стала диагональной т.е надо
подобрать такую невырожденную матрицу
S= ,
чтобы STAS=D=
,
чтобы STAS=D=
Рассмотрим в пространстве Еn линейный оператор φ такой что |φ|E=A. Поскольку матрица А симметрична, оператор φ является самосопряженным.Для этого оператора сущетсвует ортонормированный базис из собственных векторов φ, который обозначает за ε’. Как нам известно, в базисе из собственных векторов матрица линейного оператора принимает диагональный вид, причём по диагонали стоят собственные значения оператора, т.е. для S= ,
S-1AS= S – матрица перехода от ортонормированного базиса к ортонормированному и она является ортогональной.Для ортогональной матрицы ST=S-1 чтд
Таким образом для приведения квадратичной формы к каноническому виду необходимо:
Записать матрицу А данной квадратичной формы Ф
Найти собтсвенные числа соответсвующего саосопряженного оператора φ т.е. решить характерестическое уравнение |A-γE|=0 . Пусть γ1,...,γn – собственные числа. Тогда и канонический вид квадратичной формы Ф будет следующий:
Ф(x1’,…,xn’)=γ1(x1’)2+…+ γn(xn’)2
Найти собственные векторы оператора φ. Пусть это векторы а1…аn. Если все корни характерестического уравнения простые, то ти векторы образуют ортогональный базис в силу свойств самосопряженного оператора. Еси есть кратные корни то для собственных векторов , соответствующих одному собственному значению,птребуется провести процесс ортогонализации.
Из полученного ортогонального базиса сделать ортонормированный: еi=
 .
Это и будет искомый канонический базис.
.
Это и будет искомый канонический базис.
Исследование общего уравнения плоскости.
1)Общее уравнение плоскости: Ax+By+Cz+D=0 вектор n=(A,B,C)≠0
2) Плоскость перпендикулярная вектору n=(A,B,C) и проходящая через точку M0=(X0,Y0,Z0): A(x-x0)+B(y-y0)+C(z-z0)=0
3) Плоскость проходящая через 3 данные точки М1=(X1,Y1,Z1), М2=(X2,Y2,Z2), М3=(X3,Y3,Z3), не лежащие на одной прямой:
4)Плоскость отсекающая на осях координат ненулевые отрезки a,b,c описывается уравнением в отрезках:
5)Если нормальные вектор единичный, и направлен из начала координат в сторону плоскости, то получаем нормальное уравнение плоскости xcosα+ycosβ+ zcosγ-p=0 p≥0, OPперпендикулярен p, ОР^Ox=α, OP^Oy=β OP^Oz=γ. Для того чтобы общее уравнение привести к нормальному виду, его нужно умножить на μ= - нормирующий множитель, противоположен D.Р – расстояние плоскости от начала координат, cos,sin – направляющие вектора нормали
Отклонение точки М1=(X1,Y1,Z1) от плоскости L заданной нормальным уравнением, находится по формуле:
δ(M1,L)=x1cosα+y1cosβ+z1cosγ-p
Расстояние от точки М1=(X1,Y1,Z1) до плоскости L находится по формуле:
р(M1,L) =|δ(M1,L)|=| x1cosα+y1cosβ+z1cosγ-p|=
A=0 L||Ox B=0 L||Oy C=0 L||Oz D=0 L через начало координат
Вектор А0, направленный так же как и вектор А и имеющий единичную длину называется ортом вектора А А0=
Угол между плоскостями равен углу между их нормальными векторами
P1=A1x+B1y+C1z+D1=0 P2=A2x+B2y+C2z+D2=0 Cosα=
α=P1^P2 P1||P2
Условие ортогональности: Р1 перпендикулярна Р2 =0
Билет25 Классификация систем линейных уравнений по числу решений, ступенчатый вид расширенной матрицы системы в каждом случаи.
Система называется совестной если она имеет решение.В противном случаи систеа называется несовместной.
Система называется определенной, если она имеет единственное решение. Таким образом, имеется 3 варината
Система несовместна (имеет 0 решений)
Система определенная (имеет одно решение)
Система совместная неопределённая (бесконечное число решений) Ступенчатый вид расширенной матрицы.
Несовместные
rA
Совместные
rA=
Определённая rA=n

Совместные неопределённые rA<n

*-
любое число,
 - любое ненулевое число
- любое ненулевое число
Нормальное уранвение плоскости, приведение общего уравнения плоскости к нормальному.
5)Если нормальные вектор единичный, и направлен из начала координат в сторону плоскости, то получаем нормальное уравнение плоскости xcosα+ycosβ+ zcosγ-p=0 p≥0, OPперпендикулярен p, ОР^Ox=α, OP^Oy=β OP^Oz=γ. Для того чтобы общее уравнение привести к нормальному виду, его нужно умножить на μ= - нормирующий множитель, противоположен D.Р – расстояние плоскости от начала координат, cos,sin – направляющие вектора нормали
1)Общее уравнение плоскости: Ax+By+Cz+D=0 вектор n=(A,B,C)≠0
Координаты единичного вектора направляющие косинуса.
Билет26 Самосопряженный оператор и его матрица в ортонормированном базисе.
Пусть
φ линейный оператор над евклидовым
пространством Еn.
Линейный оператор φ* называется
сопряженным оператору φ, если
 Еn((φ
x,y)=(x,
φ*y)).
Еn((φ
x,y)=(x,
φ*y)).
Для всякого оператора φ существует и при том единственный сопряженный оператор φ*. Если в ортонорированном базисе оператор φ имеет матрицу А, то оператор φ* имеет матрицу АТ.
Оператор φ называется самосопряженным, если φ=φ*. Понятно что если А матрица самосопряженного оператора в ортонормированном базисе, то А=АТ. Матрица с таким свойство называется симметрической или симметричной.
Свойства самосопряженного оператора:
Матрица самосопряженного оператора влюбом ортонормированном базисе симметрична
Все характерестические числа самосопряженного оператора вещественны
Различным собственным числам самосопряженного оператора соотвествуют ортогональные собствеенные векторы
Если φ сомасопряженный оператор над Еn, то в Еn существует ортонорированный базис из собственных векторов φ, и матрица оператора в этом базисе имеет вид: где γ – собственные числа оператора φ.
Однородные системы линейных уравнений. Фундаментальная система решений.
Система линейных уравнений называется однородной, если все свободные члены равны 0
(1) AX=0 (1’)
Замечание1: Однородные системы совместны, Множество однородной системы не пусто
Теорема1:Множество решений однородной системы линейных уравнений является подпространством пространства Rn Пусть L – множество решений (1). Х,У L, требуется доказать 1) (х+у) L ; 2) α R [αx L]
x L => AX=0 => AX+AY=0 A(X+Y)=0 => X+Y L
y L => AY=0=> AX+AY=0 A(X+Y)=0
A(αX)= αAX=0 => αX L
Определение : Фундаментальной системой решений(ФСР) однородной системы линейных уравнений (1) называется базис пространства решений этой системы . Пусть ФСР = {C1…Ck} x L [x=α1C1+…+αkCk] (2)
(2)называется векторной формой записи общего решения однородной системы (1)
Нахождение ФСР 1)x1,…,xr – базисные хк+1,..,хn – свободные
2) Выражение базисных элементов через свободные
Х1= а1r+1xr+1 +…+ a1nxn
X2 = а2r+1xr+1 +…+ a2nxn (3)
Xr= = аrr+1xr+1 +…+ arnxn
Найдём общее решение в параметрической форме. Чтобы найти векторы С1,…, Ск (ФСР) придадим свободным неизвестным Хr+1,...,Xn линейно независимые наборы значений (n-r).
Хr+1,...,Xn Придадим свободным неизвестным и для каждого набора найдём частное решение r- базисных, n-r - неизвестных
С1= C2 = Cn-r= (4) X1= a1r+1Xr+1a1r+2Xr+2+…+a1nXn
Любое решение системы (1) линейно выражается через C1 , Cn X0= предположим, что этот набор решений системы (1). Стало быть его компоненты удовлетворяют системе (2) равенств
а1r+1X0r+1+…+a1nX0n (5) Из (5) Следует что = X0r+1 +…+X0n (6)
X02= а2r+1X0r+1+…+a2nX0n
X0r= аrr+1X0r+1+…+arnX0n
Из последнего (6) выражение следует что вектор
Х= = X0 r+1 +…+X0n X = X0r+1C1 +…+ X0nCn-r (7) мы получили что произвольные решения действительно равняются линейной комбинации ФСР. Векторы C1 … Cn-r образуют базис пространства решения
Размерность пространства решений однородной системы уравнений n-r где n –число неизвестных r - ранг матрицы системы
Билет 27 Ортогональный оператор и его матрица в ортонормированном базисе
Линейный оператор φ над евклидовым пространством Е называется ортогональным, если он сохраняет скалярное произведение, т.е. Е((х,у)=(φх,φу)).
Матрица А ортогонального оператора в некотором ортонормированном базисе называется также ортогональной и обладает там характерестическим свойством, что её обратная матрица совпадает с её транспонированной АТ=А-1.
Матрица перехода от ортонормированного базиса к ортонормированному является ортогональной.
Пусть
ε=(е1…еn)
и ε’ =(е’1…е’n)-
ортонормированные базисы в Е, S= ,.Тогда
по определению атрицы перехода столбцы
матрицы S
(и строки ST)
состоят из координат векторов из ε в
базисе ε’. Докажем что S
ортогональна, т.е. STS=E.
Так как ε и ε’ – ортонормированны,то
,.Тогда
по определению атрицы перехода столбцы
матрицы S
(и строки ST)
состоят из координат векторов из ε в
базисе ε’. Докажем что S
ортогональна, т.е. STS=E.
Так как ε и ε’ – ортонормированны,то
STS= =
= =E,
т.е.ST=S-1
=E,
т.е.ST=S-1
Гипербола
Гипербола- геометрическое место точек плоскости разность расстояний которых до 2х данных точек называемых фокусами есть вличина постоянная равная 2а
1)Прямая не ограниченная
|MF1-MF2|=2a c2=a2+b2 Связь между параметрами гипарболы
А1А2 – вершины гиперболы, F1F2 – фокусы
a<c y=+- bi при х=0
а- действительная ось, b - мнимая ось, с – половина фокусного расстояния
Число ε = называется эксцентриситетом гиперболы ε>1
Прямые параллельные оси Оу и имеющие уравнение называются директрисами гиперболы
Х= Левая ветвь r1-εx-a r2-εx+a
Правая ветвь r1=εx+a r2=εx-a
Прямые с уравнениями у= x называются асимптотами гиперболы
Фокальные свойства выходит будто его выпустили из другого фокуса
a=b на 45 градусов
Если гипербола равнобочная т.е. а=b , то повернутая на 45 градусов она превращается в «школьную»
Билет28 Матрица перехода от одного ортонормированного базиса к другому.
Матрица А ортогонального оператора в некотором ортонормированном базисе называется также ортогональной и обладает там характерестическим свойством, что её обратная матрица совпадает с её транспонированной АТ=А-1.
Матрица перехода от ортонормированного базиса к ортонормированному является ортогональной.
Пусть ε=(е1…еn) и ε’ =(е’1…е’n)- ортонормированные базисы в Е, S= ,.Тогда по определению атрицы перехода столбцы матрицы S (и строки ST) состоят из координат векторов из ε в базисе ε’. Докажем что S ортогональна, т.е. STS=E. Так как ε и ε’ – ортонормированны,то
STS= = =E, т.е.ST=S-1
Векторное произведение, его геометрический смысл, критерий компланарности векторов.
Упорядоченная тройка некомпланарных векторов называется правой если из конца 3его вектора кратчайший поворот от 1ого ко 2оу виден против часовой стрелки в противно случаи тройка называется левой .
Векторное произведение векторов ab называется вектор с=AxB, удовлетворяющий условиям 1
1)С перпендикулярен А; С перпендикулярен B
2) |c|=|a||b| sin(a^b)
3) A,b,c – правая тройка
Модуль векторного произведения есть площадь параллелограмма построенного на сомножителях
Векторное произведение направлено как головка буравчика который мы вращаем от 1 множителя ко 2ому
Свойства:
1)АхВ= -ВхА – анти коммутативность
2)(А+В)хС=АхС+ВхС(αА)хВ=α(АхВ)
АхВ= = i -j +k Условия коллинеарности 2 вектора коллинарны тогда и только тогда когда векторное произведение их равно 0
Компланарность
Билет 29Приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования переменных.
Пусть А матрица квадратичной формы в старом ортонормированном базисе ε. Нам необходимо подобрать такую смену базиса чтобы в новом базисе ε’ матриа квадратичной формы стала диагональной т.е надо подобрать такую невырожденную матрицу S= , чтобы STAS=D=
Рассмотрим в пространстве Еn линейный оператор φ такой что |φ|E=A. Поскольку матрица А симметрична, оператор φ является самосопряженным.Для этого оператора сущетсвует ортонормированный базис из собственных векторов φ, который обозначает за ε’. Как нам известно, в базисе из собственных векторов матрица линейного оператора принимает диагональный вид, причём по диагонали стоят собственные значения оператора, т.е. для S= ,
S-1AS= S – матрица перехода от ортонормированного базиса к ортонормированному и она является ортогональной.Для ортогональной матрицы ST=S-1 чтд
Таким образом для приведения квадратичной формы к каноническому виду необходимо:
Записать матрицу А данной квадратичной формы Ф
Найти собтсвенные числа соответсвующего саосопряженного оператора φ т.е. решить характерестическое уравнение |A-γE|=0 . Пусть γ1,...,γn – собственные числа. Тогда и канонический вид квадратичной формы Ф будет следующий:
Ф(x1’,…,xn’)=γ1(x1’)2+…+ γn(xn’)2
Найти собственные векторы оператора φ. Пусть это векторы а1…аn. Если все корни характерестического уравнения простые, то ти векторы образуют ортогональный базис в силу свойств самосопряженного оператора. Еси есть кратные корни то для собственных векторов , соответствующих одному собственному значению,птребуется провести процесс ортогонализации.
Из полученного ортогонального базиса сделать ортонормированный: еi= . Это и будет искомый канонический базис.
Различные уравнения плоскости в пространстве, расстояния от точки до плоскости.
1)Общее уравнение плоскости: Ax+By+Cz+D=0 вектор n=(A,B,C)≠0
2) Плоскость перпендикулярная вектору n=(A,B,C) и проходящая через точку M0=(X0,Y0,Z0): A(x-x0)+B(y-y0)+C(z-z0)=0
3) Плоскость проходящая через 3 данные точки М1=(X1,Y1,Z1), М2=(X2,Y2,Z2), М3=(X3,Y3,Z3), не лежащие на одной прямой:
4)Плоскость отсекающая на осях координат ненулевые отрезки a,b,c описывается уравнением в отрезках:
5)Если нормальные вектор единичный, и направлен из начала координат в сторону плоскости, то получаем нормальное уравнение плоскости xcosα+ycosβ+ zcosγ-p=0 p≥0, OPперпендикулярен p, ОР^Ox=α, OP^Oy=β OP^Oz=γ. Для того чтобы общее уравнение привести к нормальному виду, его нужно умножить на μ= - нормирующий множитель, противоположен D.Р – расстояние плоскости от начала координат, cos,sin – направляющие вектора нормали
Отклонение точки М1=(X1,Y1,Z1) от плоскости L заданной нормальным уравнением, находится по формуле:
δ(M1,L)=x1cosα+y1cosβ+z1cosγ-p
Расстояние от точки М1=(X1,Y1,Z1) до плоскости L находится по формуле:
р(M1,L) =|δ(M1,L)|=| x1cosα+y1cosβ+z1cosγ-p|=
A=0 L||Ox B=0 L||Oy C=0 L||Oz D=0 L через начало координат
Вектор А0, направленный так же как и вектор А и имеющий единичную длину называется ортом вектора А А0=
Угол между плоскостями равен углу между их нормальными векторами
P1=A1x+B1y+C1z+D1=0 P2=A2x+B2y+C2z+D2=0 Cosα=
α=P1^P2 P1||P2
Условие ортогональности: Р1 перпендикулярна Р2 =0
Расстояние от точки до плоскости
d=|M0K|=| - |=| |= d= d=
Доказать линейную зависимость:
Линейной зависимостью векторов а1,…,аn называется вектор α1а1+…+αnan где α1αn любые действительные числа
Если α1=α2=….=αn=0 то линейная комбинация – тривиальная
Система векторов а1,…,аn называется линейно зависимой если существует нетривиальная линейная комбинация этих векторов равная ненулевому вектору, в противно случаи система векторов - линейно независимая
Если b= α1а1+…+αnan , то говорят что b линейно выражается через а1,…,аn
(n≥2) Система векторов а1,…,аn называется линейно зависимой если хотя бы один из них линейно выражается через остальные, в противно случаи а1,…,аn линейно независима.
а1,…,аn – л.з.(n≥2) α1….αn не все равные 0 такие, что α1а1+…+αnan =0
Пусть α1≠0 α1а1= α2а2-…-αnan/: α1 а1= α2а2/ α1 -…-αn an/ α1 => а1= α2а2+…+αn an а1- α2а2-…- αn an=0
а1,…,аn л.з. 1) α1 ….αn не все =0 α1а1+…+αnan =0 2) n≥2 хотя бы один выражается через остальные
а1,…,аn л.н. 1) α1а1+…+αnan =0 α1=α2=….=αn=0 2) n≥2 ни один не выражается
Билет 30 Привидение уравнений линий второго порядка к каноническоу виду
Эллипс геометрическое место точек плоскости сумма, расстояний которых до 2х данных точек, называемых фокусами, есть величина постоянная равная 2а
М1F2+MF1=2a
+ =2a = (x+c)2+y2=4a2-4a +(x-c)2+y2
X2+2xc+c2=4a2-4a +x2-2xc+c2 4xc-4a2=-4a (xc-a2)2=a2 (cx-a2)2=a2(x2-2cx+c2+y2)
C2x2-2a2cx+a4=a2x2-2a2cx+a2c2+a2y2 (a2-c2)x2+a2y2=a4-a2c2 (a2-c2)x2+a2y2=a2(a2-c2) (a2-c2)>0
A2-c2=b2 обозначим b2x2+a2y2=a2b2\:a2b2
=1 – каноническое уравнение эллипса
Гипербола- геометрическое место точек плоскости разность расстояний которых до 2х данных точек называемых фокусами есть вличина постоянная равная 2а
1)Прямая не ограниченная |MF1-MF2|=2a
Парабола- геометрическое место точек равноудалённых от данной точки, называемой фокусом и от данной прямой, называемой директрисой.
Р- параметр параболы, расстояние от фокуса до директрисы MF=MK
= - каноническое уравнение параболы
Различные уравнения прямой на плоскости, геометрический смысл параметров.
1)Прямая на плоскости хОу Р хОу: z=0 P=Ax+By+Cz+D=0 если в хОу, то С=0
P=Ax+By+C =0 (1)
Теорема 1. Всякая прямая на плоскости может быть задана уравнениями вида (1) и наоборот, всякое уравнение вида (1) задаёт прямую на плоскости, поэтому уравнение вида (1) является общим уравнением плоскости. N=(A,B,C) перпендикулярно Р n=(A,B) перпендикулярно L L: Ax+By+C=0 S=(-B,A) nS=(A,B)(-B,A)=-BA+BA=0 nперпендикулярно S
Из общего уравнения (1) можно найти:
Вектор нормали к прямой n=(A,B)
Направляющие S=(-B,A)
Угол наклона прямой – угол, лежащий в верхней полуплоскости и образованный прямой с положительным направление оси Ох (α)
Угловым коэффициентом прямой называется тангенс угла наклона, относится к прямым не параллельным оси Оу
Углом между двумя прямыми, называется угол, на который нужно повернуть 1ую прямую , против часовой стрелки до совмещения её со 2ой прямой
Вектор нормали прямой называется вектор перпендикулярный прямой
Направляющий вектор параллелен прямой
Ax+By+Cz+D=0 (1) n=(A,B) S=(-B,A)
Виды уравнений прямой на плоскости
Название |
Вид уравнения |
Геометрический смысл параметра |
Общее |
Ax+By+Cz+D=0 |
N=(A,B) перпендикулн L S=(-B,A) ||L |
Уравнение прямой с угловым коэффициентом |
Y=kx+b |
K=tgα- угл. Коэфф. B- отрезок на оси Oy |
Ур.пр. проходящей через данную точку в данном направлении |
y-y0=k(x-x0) |
M1(x1,y1) L k- угловой коэффициент |
Ур. Пр. проходящей через 2 данные (.) |
|
M1(x1,y1) L М2(х2,у2) L |
Ур.Пр. в отрезках на осях |
|
а – отрезок на оси Ох , b- отр.на оси Оу |
Нормальное уравнение |
Xcosα+ysinα-p=0 |
n=(cosα,sin ) p- расстояние прямой от начала координат |
Уравнение прямой || оси Оу |
х=а |
а- отрезок на оси Ох |



 )
p-
расстояние прямой от начала координат
)
p-
расстояние прямой от начала координат
 =
= =
=

 k1≠0
k1≠0
