2. Рангом матрицы а называется максиальное число линейно-независиых строк

Все ненулевые строки в матрице ступенчатого вида линейно-независимы.

r(A)= r число ненулевых строк в ступенчатом виде.

Любая матрица приводится к ступенчатому виду элементарными преобразованиями строк:

1. Перестановка строк

2. Умножение на α≠0

3. Прибавление к одной строке другой строки, умноженной на любое число

Элементарные преобразования строк не меняют ранга матрицы

Для того чтобы найти ранг матрицы нужно привести её к ступенчатому виду, тогда число ненулевых строк в ступенчатом виде будет равняться рангу матрицы

Следствие: Максимальное число линейно независимых строк совпадает с максиальным числом линейно независимых столбцов

Сделаем элементарные преобразования столбцов r – ненулевых линейно независимых столбцов Максиальное число линейно независимых столбцов – r

Определение ранга – Ранг- максимальное число линейно независиых строк или столбцов

Для того, чтобы у системы однородной существовало еще и  нетривиальное, ненулевое   решение  необходимо и достаточно, чтобы определитель ее матрицы был равен нулю.

Билет4Комплексные числа в тригонометрической, показаедльной формах, возведение в степень и извлечение корня

Гаусс Геометрическая интерпретация комплексного числа

Сумма комплексных чисел = сумме векторов

Х= r cosα y=rsinα

Z= r(cosα+isinα) – тригонометрическая форма комплексного числа

r = |z| модуль комплексного числа α=argZ – аргумент -π≤arg Z≤π главное значение аргумента

z₁=r₁(cosα₁+isinα₁) z₂= r₂(cosα₂+i sinα₂) z₁*z₂= r₁*r₂*( cosα₁* cosα₂- sinα₁*sinα₂) + i*( cosα₁* sinα₂+ cosα₂* sinα₁)

Умножение:

z₁*z₂=r₁*r₂* (cos(α₁+ α₂) +isin(α₁+ α₂))= r₁*r₂* Деление: = (cos( +iSin( ))=

Извлечение корня:

= *Cos( +isin )= , где k=0,1,…,n-1

Возведение в степень:

Zⁿ=rⁿ* (cosnα+isinnα)= rⁿ* - формула Муавра. Каждому комплексному числу z=x+iy ставится в соответствие точка М(х,у), радиус-вектор 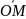которой называется геометрическим представлением комплексного числа Z. Плоскость хОу на которой изображаются комплексные числа, называется комплексной плоскостью, ось Ох – действительной осью (и поэтому обозначается Re), Oy- мнимой осью (и обозначается Im)

r=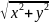 = называется модулем комплексного числа

Угол α, на который нужно повернуть положительное направление оси Ох против часовой стрелки до совмещения её с , называется аргументом комплексного числа z и обозначается Arg z. Если α= Arg z, то справедливы равенства:

Cosα= ; sinα= x=r*cosα, y=r*sinα

cosα+isinα= - формула Эйлера

z= r* - показательная форма комплексного числа

Однородные системы линейных уравнений. Фундаментальная система решений. Система линейных уравнений называется однородной, если все свободные члены равны 0

(1) AX=0 (1’)

Замечание1: Однородные системы совместны, Множество однородной системы не пусто

Теорема1:Множество решений однородной системы линейных уравнений является подпространством пространства Rⁿ Пусть L – множество решений (1). Х,У L, требуется доказать 1) (х+у) L ; 2) α R [αx L]

1. x L => AX=0 => AX+AY=0 A(X+Y)=0 => X+Y L

y L => AY=0=> AX+AY=0 A(X+Y)=0

2. A(αX)= αAX=0 => αX L

Определение : Фундаментальной системой решений(ФСР) однородной системы линейных уравнений (1) называется базис пространства решений этой системы . Пусть ФСР = {C₁…C_k} x L [x=α₁C₁+…+α_kC_k] (2)

(2)называется векторной формой записи общего решения однородной системы (1)

Нахождение ФСР 1)x₁,…,x_r – базисные х_к+1,..,х_n – свободные

2) Выражение базисных элементов через свободные

Х₁= а_1r+1x_r+1 +…+ a_1nx_n

X₂ = а_2r+1x_r+1 +…+ a_2nx_n (3)

X_r= = а_rr+1x_r+1 +…+ a_rnx_n

Найдём общее решение в параметрической форме. Чтобы найти векторы С₁,…, С_к (ФСР) придадим свободным неизвестным Х_r+1,...,X_n линейно независимые наборы значений (n-r).

Х_r+1,...,X_n Придадим свободным неизвестным и для каждого набора найдём частное решение r- базисных, n-r - неизвестных

С₁₌ C₂ = Cn-r= (4) X₁= a_1r+1X_r+1a_1r+2X_r+2+…+a_1nX_n

Любое решение системы (1) линейно выражается через C₁ , C_n X₀= предположим, что этот набор решений системы (1). Стало быть его компоненты удовлетворяют системе (2) равенств

а_1r+1X_0r+1+…+a_1nX_0n (5) Из (5) Следует что = X_0r+1 +…+X_0n (6)

X₀₂= а_2r+1X_0r+1+…+a_2nX_0n

X_0r= а_rr+1X_0r+1+…+a_rnX_0n

Из последнего (6) выражение следует что вектор

Х= = X_{0 r+1} +…+X_0n X = X_0r+1C₁ +…+ X_0nC_n-r (7) мы получили что произвольные решения действительно равняются линейной комбинации ФСР. Векторы C₁ … C_n-r образуют базис пространства решения

Размерность пространства решений однородной системы уравнений n-r где n –число неизвестных r - ранг матрицы системы