4 Вопрос

Замечательные пределы. Методы раскрытия неопределенностей

1 Первый замечательный предел

Функция не определена при x=0, так как числитель и знаменатель дроби обращаются в нуль. График функции изображен на рисунке.

Однако, можно найти предел этой функции при х→0.

П риведем доказательство записанной формулы. Рассмотрим окружность радиуса 1 и предположим, что угол α, выраженный в радианах, заключен в пределах 0 < α < π/2. (Так как четная функция и ее значения не изменяются при изменении знака α, то достаточно рассмотреть случай, когда α > 0.) Из рисунка видно, что

S_ΔOAC <S_сект.OAC <S_ΔOBC.

Так как указанные площади соответственно равны

S_ΔOAC=0,5∙OC∙OA∙sinα=0,5sinα,S_сект.OAC=0,5∙OC²∙α=0,5α,S_ΔOBC=0,5∙OC∙BC=0,5tgα.

Следовательно,

sin α < α < tg α.

Разделим все члены неравенства на sin α > 0:

.

Но . Поэтому на основании теоремы 4 о пределах заключаем, что .

Выведенная формула и называется первым замечательным пределом.

Таким образом, первый замечательный предел служит для раскрытия неопределенности . Заметим, что полученную формулу не следует путать с пределами .

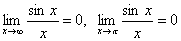2 Второй замечательный предел

Второй замечательный предел служит для раскрытия неопределенности 1^∞ и выглядит следующим образом

Обратим внимание на то, что в формуле для второго замечательного предела в показателе степени должно стоять выражение, обратное тому, которое прибавляется к единице в основании (так как в этом случае можно ввести замену переменных и свести искомый предел ко второму замечательному пределу).

Примеры.

1. .

2. .

3. .

4. .

5. .

6. .

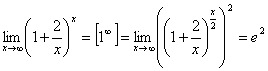3

Условные выражения

характеризуют типы неопределенностей и применяются для обозначения переменных величин, при вычислении предела которых нельзя сразу применять общие свойства пределов.

Рассмотрим некоторые приемы раскрытия неопределенностей.

I. Неопределенность .

1. .

2. .

При разложении числителя на множители воспользовались правилом деления многочлена на многочлен «углом». Так как число x=1 является корнем многочлена x³ – 6x² + 11x– 6, то при делении получим

3. 

4. 

5. .

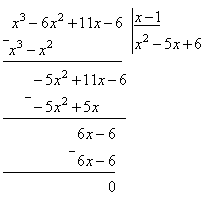
II. Неопределенность .

1. .

При вычислении предела числитель и знаменатель данной дроби разделили на x в старшей степени.

2. .

3. .

4. .

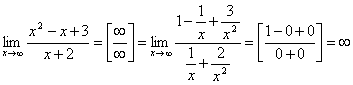При вычислении предела воспользовались равенством ,если x<0.

Следующие виды неопределенностей с помощью алгебраических преобразований функции, стоящей под знаком предела, сводят к одному из рассмотренных выше случаев или .

III. Неопределенность 0 ·∞.

.

IV. Неопределенность ∞ –∞.

5 Вопрос

Предел функции в точке, существование и единственность предела, бесконечно малые фун-ии

1 Предел функции в точке

Функция y=f(x) стремится к пределу b при x → a, если для каждого положительного числа ε, как бы мало оно не было, можно указать такое положительное число δ, что при всех x ≠ a из области определения функции, удовлетворяющих неравенству |x - a| < δ, имеет место неравенство |f(x) - b| < ε. Если b есть предел функции f(x) при x → a, то пишут или f(x) → b при x → a.

Проиллюстрируем это определение на графике функции. Т.к. из неравенства |x - a| < δ должно следовать неравенство |f(x) - b| < ε, т.е. при x  (a - δ, a + δ) соответствующие значения функции f(x)  (b - ε, b + ε), то, взяв произвольное ε > 0, мы можем подобрать такое число δ, что для всех точек x, лежащих в δ – окрестности точки a, соответствующие точки графика функции должны лежать внутри полосы шириной 2ε, ограниченной прямыми y = b – ε и y = b + ε.

Несложно заметить, что предел функции должен обладать теми же свойствами, что и предел числовой последовательности, а именно и если при x → a функция имеет предел, то он единственный.