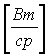- •7. Плоская световая волна, ее характеристики: амплитуда, фаза, волновой фронт и другие. Частота, длина волны, скорость волны: в вакууме и в оптической среде.
- •15 . Интерференция света в тонких пленках
- •16 Кольца Ньютона. Наблюдение в проходящем и отражённом свете
- •Дифракция как явление и как свойство света. Угол дифракции — мера расходимости ограниченного светового пучка.
- •Дифракция сферической волны на круглом отверстии. Зоны Френеля.
- •Зоны Френеля. Зонная пластинка. Растровая фокусирующая оптика.
- •27.Дифракционная решётка. Уравнение дифракционной решётки. Порядки дифракции. Условие наблюдения дифракционной картины.
- •41. Круговая (циркулярная) и эллиптическая поляризация света
- •45. Искусственная анизотропия
1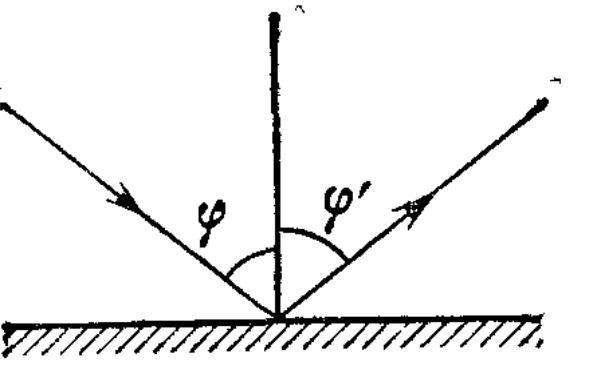 Оптика
- учение о природе света, световых
явлениях и взаимодействии света с
веществом. И почти вся ее история - это
история поиска ответа: что такое свет?
Одна из первых теорий света - теория
зрительных лучей - была выдвинута
греческим философом Платоном. Данная
теория предполагала, что из глаза исходят
лучи, которые, встречаясь с предметами,
освещают их и создают видимость
окружающего мира. Взгляды Платона
поддерживали многие ученые древности
и, в частности, Евклид, исходя из теории
зрительных лучей, основал учение о
прямолинейности распространения света,
установил закон отражения. В те же годы
были открыты следующие факты: -
прямолинейность распространения света;
явление отражения света и закон отражения;
явление преломления света; фокусирующее
действие вогнутого зеркала. Древние
греки положили начало
отрасли оптики, получившей позднее
название геометрической. Оптика
– раздел физики, изучающий свойства и
физическую природу света, а также его
взаимодействие с веществом. Основные
законы геометрической оптики были
известны задолго до установления
физической природы света.
Закон
прямолинейного распространения света:
в оптически однородной среде свет
распространяется прямолинейно. До-во
.опыт по прохождению света далекого
источника сквозь небольшое отверстие,
в результате чего образуется узкий
световой пучок. Этот опыт приводит к
представлению о световом луче как о
геометрической линии, вдоль которой
распространяется свет.
Закон
отражения света:
падающий и отраженный лучи, а также
перпендикуляр к границе раздела двух
сред, восстановленный в точке падения
луча, лежат в одной плоскости (плоскость
падения).
Угол отражения γ равен углу падения α.
Оптика
- учение о природе света, световых
явлениях и взаимодействии света с
веществом. И почти вся ее история - это
история поиска ответа: что такое свет?
Одна из первых теорий света - теория
зрительных лучей - была выдвинута
греческим философом Платоном. Данная
теория предполагала, что из глаза исходят
лучи, которые, встречаясь с предметами,
освещают их и создают видимость
окружающего мира. Взгляды Платона
поддерживали многие ученые древности
и, в частности, Евклид, исходя из теории
зрительных лучей, основал учение о
прямолинейности распространения света,
установил закон отражения. В те же годы
были открыты следующие факты: -
прямолинейность распространения света;
явление отражения света и закон отражения;
явление преломления света; фокусирующее
действие вогнутого зеркала. Древние
греки положили начало
отрасли оптики, получившей позднее
название геометрической. Оптика
– раздел физики, изучающий свойства и
физическую природу света, а также его
взаимодействие с веществом. Основные
законы геометрической оптики были
известны задолго до установления
физической природы света.
Закон
прямолинейного распространения света:
в оптически однородной среде свет
распространяется прямолинейно. До-во
.опыт по прохождению света далекого
источника сквозь небольшое отверстие,
в результате чего образуется узкий
световой пучок. Этот опыт приводит к
представлению о световом луче как о
геометрической линии, вдоль которой
распространяется свет.
Закон
отражения света:
падающий и отраженный лучи, а также
перпендикуляр к границе раздела двух
сред, восстановленный в точке падения
луча, лежат в одной плоскости (плоскость
падения).
Угол отражения γ равен углу падения α.
Закон
преломления света:
падающий и преломленный лучи, а также
перпендикуляр к границе раздела двух
сред, восстановленный в точке падения
луча, лежат в одной плоскости. Отношение
синуса угла падения α к синусу угла
преломления β есть величина, постоянная
для двух данных сред
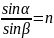 .Постоянную
величину n называют относительным
показателем преломления второй среды
относительно первой. Показатель
преломления среды относительно вакуума
называют абсолютным показателем
преломления. Относительный показатель
преломления двух сред равен отношению
их абсолютных показателей преломления:
n=n2/n1.
Среду с меньшим абсолютным показателем
преломления называют
оптически менее плотной.
Законы
отражения и преломления: γ = α;
n1 sin α = n2 sin β.
.Постоянную
величину n называют относительным
показателем преломления второй среды
относительно первой. Показатель
преломления среды относительно вакуума
называют абсолютным показателем
преломления. Относительный показатель
преломления двух сред равен отношению
их абсолютных показателей преломления:
n=n2/n1.
Среду с меньшим абсолютным показателем
преломления называют
оптически менее плотной.
Законы
отражения и преломления: γ = α;
n1 sin α = n2 sin β.
3 Пусть
абсолютный показатель преломления
первой среды больше, чем абсолютный
показатель преломления второй среды,
n1>n2
то есть первая среда оптически более
плотная. Здесь абсолютные показатели
сред соответственно равны:
Пусть
абсолютный показатель преломления
первой среды больше, чем абсолютный
показатель преломления второй среды,
n1>n2
то есть первая среда оптически более
плотная. Здесь абсолютные показатели
сред соответственно равны:
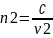 Тогда, если направить луч света из
оптически более плотной среды в оптически
менее плотную
среду,
то по мере увеличения угла
падения преломленный луч будет
приближаться к границе раздела двух
сред (рис.1), затем пойдет по границе
раздела (рис.2), а при дальнейшем увеличении
угла падения преломленный луч исчезнет,
т.е.падающий луч будет полностью
отражаться границей раздела
двух сред (рис.3)).
Тогда, если направить луч света из
оптически более плотной среды в оптически
менее плотную
среду,
то по мере увеличения угла
падения преломленный луч будет
приближаться к границе раздела двух
сред (рис.1), затем пойдет по границе
раздела (рис.2), а при дальнейшем увеличении
угла падения преломленный луч исчезнет,
т.е.падающий луч будет полностью
отражаться границей раздела
двух сред (рис.3)).
Предельный
угол
(альфа
нулевое)–
это угол падения, которому соответствует
угол преломления 90 градусов.
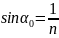 Приборы
и устройства,
в которых используется явление полного
отражения:
-
поворотная призма - в перископе
Приборы
и устройства,
в которых используется явление полного
отражения:
-
поворотная призма - в перископе

-
оборотная призма – в бинокле
 -
оптическое волокно – в световодах
(тонких кварцевых или пластмассовых
нитях диаметром 50-500 мкм в оболочке из
того же вещества, но с меньшим
показателем преломления),
где
информация передается как
последовательность световых
импульсов.
Проявления
в природе:
-
пузырьки воздуха на подводных
растениях кажутся зеркальными
- капли
росы вспыхивают разноцветными огнями
-
«игра» бриллиантов в лучах света
-
поверхность воды в стакане при
рассматривании снизу через стенку
стакана будет блестеть.
-
оптическое волокно – в световодах
(тонких кварцевых или пластмассовых
нитях диаметром 50-500 мкм в оболочке из
того же вещества, но с меньшим
показателем преломления),
где
информация передается как
последовательность световых
импульсов.
Проявления
в природе:
-
пузырьки воздуха на подводных
растениях кажутся зеркальными
- капли
росы вспыхивают разноцветными огнями
-
«игра» бриллиантов в лучах света
-
поверхность воды в стакане при
рассматривании снизу через стенку
стакана будет блестеть.
4.

5.
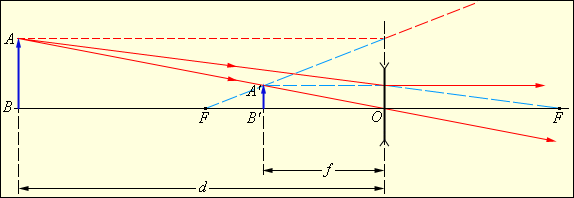
Формула тонкой линзы-связывает
расстояние d
от линзы до источника расстояния f
от линзы до изображения :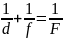 . Эта формула может применяется для
действительных и мнимых изображений
как в случае собирающей линзы, так и
для рассеивающей, если считать: F>0
для собирающей линзы, F<0
для рассеивающей, f>0
действительного изображения, f<0
для мнимого. Величина d
положительна, если на линзу падает
расходящийся пучок лучей (действительный
источник ) и отрицательна, если пучок
сходящийся (продолжение лучей пересекаются
за линзой в месте нахождения “мнимого”
источника). Увеличение
линзы Г
называется отношение линейных размеров
изображения H
и предмета h
,т.е. Г=Н/h.
Выполняется соотношение Г=
. Эта формула может применяется для
действительных и мнимых изображений
как в случае собирающей линзы, так и
для рассеивающей, если считать: F>0
для собирающей линзы, F<0
для рассеивающей, f>0
действительного изображения, f<0
для мнимого. Величина d
положительна, если на линзу падает
расходящийся пучок лучей (действительный
источник ) и отрицательна, если пучок
сходящийся (продолжение лучей пересекаются
за линзой в месте нахождения “мнимого”
источника). Увеличение
линзы Г
называется отношение линейных размеров
изображения H
и предмета h
,т.е. Г=Н/h.
Выполняется соотношение Г= .
.
 3
3
OF=F-
фокусное расстояние.d-расстояние
от объекта до линзы. f-расстояние
от линзы до изображения. F-
фокусное расстояние линзы. Решение-
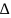 BDO
подобен
OB1A1
BDO
подобен
OB1A1
BO1/OB1=AB/A1B1 (1) COF падает FB1A1 => CO/A1B1=OF/FB1 (CO=AB) => AB/A1B1=OF/FB посмотри на (1) =>BO/OB1=OF/FB1 фигурная скобка(BO=d; OB1=f; OF=F;)
=>d/f=f/(f-F) ; => d(f-F)=Ff; => df-df=Ff; Учитывая св-во пропорции, имеем Ff+Fd=fd; Поделив все члены полученого равенства на произведение Ffd получим 1/d+1/f=1/F
6. Формула тонкой линзы-связывает расстояние d от линзы до источника расстояния f от линзы до изображения : . Эта формула может применяется для действительных и мнимых изображений как в случае собирающей линзы, так и для рассеивающей, если считать: F>0 для собирающей линзы, F<0 для рассеивающей, f>0 действительного изображения, f<0 для мнимого. Величина d положительна, если на линзу падает расходящийся пучок лучей (действительный источник ) и отрицательна, если пучок сходящийся (продолжение лучей пересекаются за линзой в месте нахождения “мнимого” источника). Увеличение линзы Г называется отношение линейных размеров изображения H и предмета h ,т.е. Г=Н/h. Выполняется соотношение Г= .
7. Плоская световая волна, ее характеристики: амплитуда, фаза, волновой фронт и другие. Частота, длина волны, скорость волны: в вакууме и в оптической среде.
Волна называется плоской, если ее волновые повеpхности пpедставляют собой паpаллельные дpуг дpугу плоскости, пеpпендикуляpные фазовой скоpости волны .Следовательно, лучи плоской волны - суть паpаллельные пpямые.
Уравнение плоской волны.
Пусть
в начале координат находится твердая
плоскость, которая колеблется по
гармоническому закону и вынуждает
частицы упругой среды, находящейся
рядом с ней, колебаться по этому же
закону. Направим ось x перпендикулярно
этой плоскости. Тогда вдоль этой оси
будет распространяться плоская
гармоническая продольная волна. Наша
задача - найти ![]() -
уравнение волны, если задано
-
уравнение волны, если задано ![]() .
.
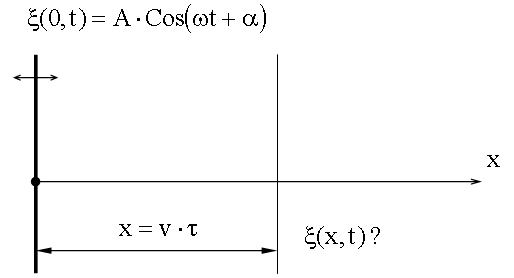
Колебания
до волновой поверхности, удаленной от
начала координат на расстояние x,
дойдут через время ![]() ,
значит уравнение волны
,
значит уравнение волны
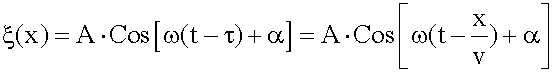 .
.
Фаза волны
- это аргумент у косинуса в уравнении волны, т.е.
 ,
,
Фаза плоской волны зависит от двух переменных - x и t.
Фазовая скорость
- это скорость перемещения в пространстве поверхности, вдоль которой фаза волны остается постоянной, т.е.
 .
.
Найдем производную от этого выражения по времени:
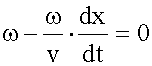 ,
,
откуда искомая фазовая скорость волны:
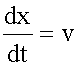 .
.
Уравнение плоской волны,
распространяющейся в направлении, противоположном оси x:
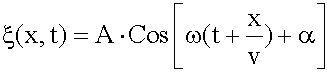 .
.
Из (15.2.2) для этой волны:
 .
.
Волновое число, симметричная форма уравнения волны
 .
.
Введем
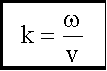 -
волновое число.
-
волновое число.
Тогда
![]() .
.
При такой записи координата х и время t входят в уравнение волны симметрично.
8. Волна, радиально расходящаяся от источника или сходящаяся к приёмнику; волн. фронт её — сфера. Простейшим примером явл. гармонич. симметричная С. в. в среде без поглощения:
![]()
где r — расстояние от источника, А/r — амплитуда, w±kr — фаза волны, w — круговая частота, А — волн. число. По мере удаления от источника значение |u2(r, t)| убывает как 1/r2. Но т. к. плотность потока энергии волны S=|u(r, t)|2, то вследствие закона сохранения энергии полная мощность S0•4pr2, уносимая от центра расходящейся волной (или приходящая к нему в сходящейся волне), остаётся постоянной. С. в. (1) — одно из решений трёхмерного волнового уравнения. При отсутствии дисперсии волн общее сферически симметричное решение этого ур-ния можно представить как суперпозицию сходящихся и расходящихся волн вида:
u(r, t)=(1/r)f(t±r/v), (2)
где f(t±r/v) — нек-рое стационарное возмущение, удовлетворяющее однородному волн. ур-нию, v — фазовая скорость.
Несимметричной С. в. наз. волна со сферич. фазовыми фронтами, амплитуда к-рой зависит от полярной q и азимутальной j координат:
u(t, q, j, t) =u(r, t)y(q, j), (3)
где u(r, t) — волн. возмущение, напр. в форме (1) или (2), а y(q, j) — суперпозиция сферич. гармоник. В однородной среде на больших расстояниях от источника волн. поле почти всегда имеет вид (3). Подбором распределения y(q, j) можно сконцентрировать поле внутри определ. телесного угла. Так формируется направление излучения волн, напр. в антеннах.
СФЕРИЧЕСКАЯ ВОЛНА
-
волна, радиально расходящаяся от нек-рой
точки (источника) или сходящаяся к ней
(к стоку) и имеющая сферич. волновые
фронты (поверхности равных фаз). Простейшим
примером является сферически симметричная
скалярная волна вида: u=f(r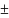 ct)/r
ct)/r
расходящаяся от центр. точки r = 0 (знак "-") или сходящаяся к ней (знак "+") со скоростью с. Такая волна удовлетворяет волновому уравнению и описывает многие физ. процессы в линейных средах без дисперсии и без потерь. Суперпозиция сходящейся и расходящейся волн (в частности, стоячая С. в.) также является решением волнового ур-ния.
Ф-ция f в общем случае произвольна; важный частный случай - гармоническая С. в.: f=Aexpi(wt + kr); в такой волне А/r - амплитуда, а wt + kr= Ф - фаза (w - круговая частота, k - волновое число).
Если величина u(r, t )описывает физ. поле (напр., возмущение давления в звуковой волне, скалярный потенциал в эл.-магн. волне и др.), то плотность потока энергии поля, уносимой от источника или приносимой к нему, пропорц. |u(r, t)|2, и, следовательно, общий поток энергии через сферу любого радиуса r, пропорц. 4pr2| и|2, сохраняется неизменным. Это является следствием закона сохранения энергии.
При наличии поглощения в среде энергия С. в. убывает в направлении её распространения. Для гармонии. С. в. поглощение может быть учтено заменой k на k' + k ", где k " - мнимая часть волнового числа. Это означает, что амплитуда волны затухает по экспоненте:
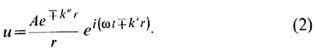
Существуют и несимметричные С. в., амплитуды к-рых зависят от полярной q и азимутальной j угл. координат, но фазовые фронты по-прежнему остаются сферическими:

где U(r, t )отвечает симметричной С. в., напр. в форме (1) или (2), a D(q,j) описывает угл. зависимость поля (эту ф-цию можно представить в виде суперпозиции т. н. сферич. гармоник). В однородных изотропных средах волновое поле на больших расстояниях от центра почти всегда имеет вид (3). Подбором D можно концентрировать поле около заданных направлений, поэтому ф-ция D(q, j) наз. диаграммой направленности излучения источника.
Волна называется сферической, если её волновые поверхности — сферы Понятие сферической волны оказывается чрезвычайно полезным. В самом деле, возьмём прозрачную однородную среду, физические свойства которой одинаковы вдоль всех направлений. Точечный источник света, помещённый в такую среду, излучает сферические волны (это понятно — ведь свет пойдёт в каждом направлении с одинаковой скоростью, так что любая волновая поверхность будет сферой). Ну а протяжённый источник света можно рассматривать как совокупность точечных источников, и наложение сферических волн этих источников даст общую световую волну, идущую от протяжённого источника.Кроме того, обсуждаемые ниже вторичные волны (центральное понятие принципа Гюйгенса) являются именно сферическими.
9 Электромагнитная волна называется монохроматической, если переменные поля меняются со временем по гармоническому закону. Для плоской монохроматической волны
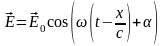 .
(9.8)
.
(9.8)
Здесь
 - амплитуда, циклическая частота и
начальная фаза, соответственно. Начальную
фазу удобно сразу принять за нуль (выбор
начала отсчета времени). Введем волновое
число
- амплитуда, циклическая частота и
начальная фаза, соответственно. Начальную
фазу удобно сразу принять за нуль (выбор
начала отсчета времени). Введем волновое
число
 .
(9.9)
.
(9.9)
Тогда
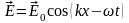 .
(9.10)
.
(9.10)
Если ввести волновой вектор
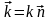 ,
(9.11)
,
(9.11)
то последнюю формулу можно представить в виде:
 .
(9.12)
.
(9.12)
Последняя
формула описывает волну, распространяющуюся
в произвольном фиксированном направлении,
которое задается единичным вектором
 .
.
. Для плоской монохроматической линейно поляризованной волны окончательно имеем:
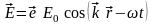 .
(9.13)
.
(9.13)
В общем случае плоская монохроматическая волна (9.12) представляет собой суперпозицию двух линейно поляризованных волн:
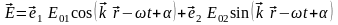 .
(9.14)
.
(9.14)
Шкала электромагнитных волн:
Радиоволны
=105- 1011 Гц, =10-3-103 м.
Получают с помощью колебательных контуров и макроскопических вибраторов. Свойства. Радиоволны различных частот и с различными длинами волн по-разному поглощаются и отражаются средами. Применение Радиосвязь, телевидение, радиолокация. В природе радиоволны излучаются различными внеземными источниками (ядра галактик, квазары).
Инфракрасное излучение (тепловое)
=3-1011- 4.1014 Гц, =8.10-7 - 2.10-3 м.
Излучается атомами и молекулами вещества.
Инфракрасное излучение дают все тела при любой температуре.
Человек излучает электромагнитные волны 9.10-6 м.
Свойства
1. Проходит через некоторые непрозрачные тела, а также сквозь дождь, дымку, снег.
2. Производит химическое действие на фотопластинки.
3. Поглощаясь веществом, нагревает его.
4. Вызывает внутренний фотоэффект у германия.
5. Невидимо.
Регистрируют тепловыми методами, фотоэлектрическими и фотографическими.
Применение. Получают изображения предметов в темноте, приборах ночного видения (ночные бинокли), тумане. Используют в криминалистике, в физиотерапии, в промышленности для сушки окрашенных изделий, стен зданий, древесины, фруктов.
Видимое излучение
Часть электромагнитного излучения, воспринимаемая глазом (от красного до фиолетового):
Свойства. Воздействует на глаз.
Ультрафиолетовое излучение
![]()
(меньше, чем у фиолетового света)
Источники: газоразрядные лампы с трубками из кварца (кварцевые лампы).
Излучается всеми твердыми телами, у которых T>1000°С, а также светящимися парами ртути.
Рентгеновские лучи
Излучаются при большом ускорении электронов, например их торможение в металлах. Получают при помощи рентгеновской трубки: электроны в вакуумной трубке (р= 10-3-10-5 Па) ускоряются электрическим полем при высоком напряжении, достигая анода, при соударении резко тормозятся. При торможении электроны движутся с ускорением и излучают электромагнитные волны с малой длиной (от 100 до 0,01 им).Свойства Интерференция, дифракция рентгеновских лучей на кристаллической решетке, большая проникающая способность. Облучение в больших дозах вызывает лучевую болезнь. -излучение
Источники: атомное ядро (ядерные реакции). Свойства. Имеет огромную проникающую способность, оказывает сильное биологическое воздействие. Применение. В медицине, производстве (дефектоскопия). Применение. В медицине, в промышленности.
Шкала электромагнитных волн представляет собой непрерывную последовательность частот и длин электромагнитных излучений, представляющих собой распространяющееся в пространстве переменное магнитное поле. Теория электромагнитных явлений Джеймса Максвелла позволила установить, что в природе существуют электромагнитные волны разных длин.
.
Световым
полем называют электромагнитное поле
в оптическом
диапазоне частот.
Оптические частоты чрезвычайно велики
(порядка
в оптическом диапазоне свет очень слабо взаимодействует с веществом. Для частот, более низких, чем частоты оптического диапазона, нельзя построить оптические системы по законам геометрической оптики, а электромагнитное поле более высоких частот, как правило, либо проходит сквозь любое вещество, либо разрушает его.Оптический диапазон состоит из следующих видов излучения: рентгеновское, ультрафиолетовое (УФ), видимое, инфракрасное (ИК). Если во времена Ньютона в оптический диапазон входило только видимое излучение, то с техническим прогрессом диапазон существенно расширился, причем рентгеновское излучение включено в оптический диапазон совсем недавно - примерно 20 лет назад. |
10
Поток излучения (лучистый
поток) ![]() -
это величина энергии, переносимой полем
в единицу времени через данную площадку
(рис.2.1.1)
-
это величина энергии, переносимой полем
в единицу времени через данную площадку
(рис.2.1.1)
Поток
излучения измеряется в ваттах: ![]() , .
, .

 Рис.
2.1.1. Поток излучения.
Рис.
2.1.1. Поток излучения.
Спектральная
плотность потока излучения ![]() -
это функция, показывающая распределение
энергии по спектру излучения:
-
это функция, показывающая распределение
энергии по спектру излучения:
|
Тогда
общий суммарный поток для всех длин
волн в диапазоне от ![]() до
до ![]() будет
вычисляться как интеграл:
будет
вычисляться как интеграл:
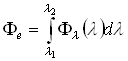 Поверхностная
плотность потока энергии
Поверхностная
плотность потока энергии ![]() -
это величина потока, приходящегося на
единицу площади:
-
это величина потока, приходящегося на
единицу площади:
|
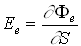
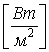 Если
площадка освещается потоком,
то поверхностная плотность потока
энергии будет иметь
смысл энергетическойосвещенности или облученности
.Если
поток излучается площадкой,
то поверхностная плотность потока
энергии будет иметь смысл энергетической
светимости
Если
площадка освещается потоком,
то поверхностная плотность потока
энергии будет иметь
смысл энергетическойосвещенности или облученности
.Если
поток излучается площадкой,
то поверхностная плотность потока
энергии будет иметь смысл энергетической
светимости ![]() .
.
Спектральная
плотность поверхностной плотности
потока ![]() показывает
распределение светимости или освещенности
по спектру излучения:
показывает
распределение светимости или освещенности
по спектру излучения:
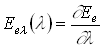 Рассмотрим
излучение точечного источника в пределах
некоторого телесного угла
Рассмотрим
излучение точечного источника в пределах
некоторого телесного угла ![]() (рис.2.1.3):
(рис.2.1.3):
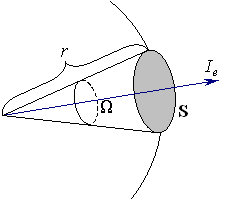 Рис.2.1.3.
Энергетическая сила света.
Рис.2.1.3.
Энергетическая сила света.
Телесный
угол данного
конуса равен отношению площади ![]() поверхности,
вырезанной на сфере конусом, к квадрату
радиуса
поверхности,
вырезанной на сфере конусом, к квадрату
радиуса ![]() сферы.
сферы.
|
Телесный
угол измеряется в стерадианах (в
сфере ![]() ).
).
Сила излучения (энергетическая сила света) - это поток излучения, приходящийся на единицу телесного угла, в пределах которого он распространяется:
|
За
единицу энергетической силы света
приняты сила излучения такого точечного
источника, у которого в пределах ![]() равномерно
распределяется поток излучения
в
равномерно
распределяется поток излучения
в ![]() . Освещенностью поверхности
называется величина, равная световому
потоку, падающему на единицу площади
равномерно освещаемой поверхности.В
СИ освещенность измеряется в люксах
(лк). Первый
закон освещенности:
освещенность поверхности точечным
источником прямо пропорциональна силе
света источника и обратно пропорциональна
квадрату расстояния от источника до
освещаемой поверхности:
. Освещенностью поверхности
называется величина, равная световому
потоку, падающему на единицу площади
равномерно освещаемой поверхности.В
СИ освещенность измеряется в люксах
(лк). Первый
закон освещенности:
освещенность поверхности точечным
источником прямо пропорциональна силе
света источника и обратно пропорциональна
квадрату расстояния от источника до
освещаемой поверхности:
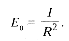 Второй
закон освещенности:
освещенность поверхности прямо
пропорциональна косинусу угла падения
лучей:
Второй
закон освещенности:
освещенность поверхности прямо
пропорциональна косинусу угла падения
лучей:
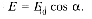 Объединенный
закон освещенности:
освещенность, создаваемая точечным
источником света на некоторой
площадке, прямо
пропорциональна силе
света источника и косинусу угла падения
лучей и обратно
пропорциональна квадрату
расстояния до площадки от источника:
Объединенный
закон освещенности:
освещенность, создаваемая точечным
источником света на некоторой
площадке, прямо
пропорциональна силе
света источника и косинусу угла падения
лучей и обратно
пропорциональна квадрату
расстояния до площадки от источника:
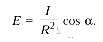
11 На рис. 1 кривая видности изображена для цветного зрения. Максимум кривой при =555 нм означает, что чувствительность глаза к свету вблизи этой области длин волн (в желто-зеленой части спектра) наибольшая.
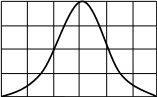
Vλ 1.0
0.5
400 550 700 λ, нм
Принято считать, что функция видности для этой длины волны равна единице, V(555нм) = 1, но при таком же потоке энергии оцениваемая зрительно интенсивность света для других длин волн меньше, а потому меньше и значение функции видности. Кривая построена так, что
V(1)/V(2) = (dэ)2 /(dэ)1.
Например, чтобы зрительные ощущения были одинаковыми энергия света для = 510 нм и = 610 нм должна быть вдвое больше, чем энергия света с = 555 нм. При 388 нм и >780 нм функция видности равна нулю, т.е. глаз эти волны не видит, хотя они и несут с собой энергию.
Из сказанного следует, что субъективная оценка интенсивности света отличается от объективной - энергетической. Но с помощью кривой видности можно установить связь между этими оценками. Для этого вводят понятие светового потока dФ
dФ = V()dФэ
Так как функция видности безразмерна, то можно сказать, что световой поток – это поток лучистой энергии, оцениваемый по зрительному ощущению.
Если источник точечный, то под силой света I понимают световой поток, распространяющийся в единице телесного угла (рис. 2)
I = dФ/d. n
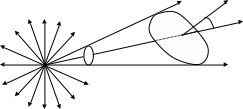
i
σ
L
dΩ
Для анизотропного источника света связь светового потока с силой света в полярной системе координат описывается формулой
dФ = Iθ,φ sin θ dθ dφ.
В случае равномерного потока эта связь упрощается Ф = 4π I.
Величина полного светового потока характеризует излучающий источник, и её нельзя увеличить никакими оптическими системами. Действие этих систем может сводиться лишь к перераспределению светового потока.
В системе СИ принята единица силы света кандела (кд) – одна из основных единиц (ГОСТ).
«Кандела – сила света, испускаемая с площади 1/600000 м2 полного излучателя (эталона) в перпендикулярном этому сечению направлении при температуре излучателя равном температуре затвердевания платины при давлении 101325 Па».
За единицу светового потока принимают люмен (лм). Это поток, излучаемый изотропным источником силой в 1кд в пределах телесного угла в 1 стерадиан.
Ф = I (1лм = 1кд 1ср)
Из опыта известно, что если = 555 нм, то одному люмену светового потока соответствует поток лучистой энергии равный 0,0016 Вт. Это механический эквивалент света (А555 = 0,0016 Вт/лм). Если 555 нм, то механический эквивалент будет равен
Аλ=А555/V() Вт/лм
Если источник света не является точечным, то его принято характеризовать яркостью в данном направлении.
Вi = dФ/σ cos i dΩ
Итак, яркостью в данном направлении называется световой поток, посылаемый в данном направлении единицей видимой поверхности внутрь единичного телесного угла (рис.3).
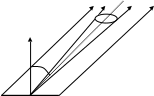
dΩ
n
i
σ Рис. 3
Яркость Вi есть величина, зависящая от направления; однако для некоторых источников она может от направления не зависеть. Такие источники называются источниками, подчиняющимися закону Ламберта.
Единицей яркости служит яркость площадки, дающая силу света в 1 кд с каждого квадратного метра в направлении, перпендикулярном к площадке.
Таким образом, единица яркости есть "кандела с квадратного метра" - иначе её называют нит (нт).
Светимость представляет собой интегральную величину, т.е. суммарный световой поток, посылаемый единицей поверхности в полупространство (внутрь телесного угла 2π стерадиан).
Светимость и яркость связаны между собой простым соотношением

12 Электромагнитная волна называется монохроматической, если переменные поля меняются со временем по гармоническому закону. Для плоской монохроматической волны
. (9.8)
Здесь - амплитуда, циклическая частота и начальная фаза, соответственно. Начальную фазу удобно сразу принять за нуль (выбор начала отсчета времени). Введем волновое число
. (9.9)
Тогда
. (9.10)
Если ввести волновой вектор
, (9.11)
то последнюю формулу можно представить в виде:
. (9.12)
Последняя формула описывает волну, распространяющуюся в произвольном фиксированном направлении, которое задается единичным вектором .
Пусть
вектор
 в электромагнитной волне остается в
процессе ее распространения параллельным
некоторому постоянному вектору
в электромагнитной волне остается в
процессе ее распространения параллельным
некоторому постоянному вектору
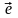 ,
который называется вектором поляризации.
В этом случае волна называется линейно
поляризованной. Для плоской монохроматической
линейно поляризованной волны окончательно
имеем:
,
который называется вектором поляризации.
В этом случае волна называется линейно
поляризованной. Для плоской монохроматической
линейно поляризованной волны окончательно
имеем:
. (9.13)
В общем случае плоская монохроматическая волна (9.12) представляет собой суперпозицию двух линейно поляризованных волн:
. (9.14)
Здесь
векторы
 - постоянные векторы перпендикулярные
друг другу и перпендикулярные направлению
распространению волны (т.е. вектору
).
- постоянные векторы перпендикулярные
друг другу и перпендикулярные направлению
распространению волны (т.е. вектору
).
Пусть
волна распространяется вдоль оси
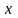 .
Далее, предположим, что вектор
.
Далее, предположим, что вектор
 направлен вдоль оси
направлен вдоль оси
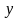 ,
а вектор
,
а вектор
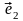 направлен вдоль оси
направлен вдоль оси
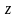 .
Тогда
.
Тогда
 .
.
Исключая из двух последних равенств время, найдем
 .
(9.15)
.
(9.15)
Последнее
равенство показывает, что в плоскости
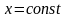 вектор
вращается так, что его конец описывает
эллипс. Поскольку распространение
электромагнитной волны происходит в
направлении оси
,
то изменение вектора
в пространстве и во времени представляется
в виде движения его конца по эллиптической
спирали (эллиптически поляризованная
волна). Шаг спирали равен длине волны
вектор
вращается так, что его конец описывает
эллипс. Поскольку распространение
электромагнитной волны происходит в
направлении оси
,
то изменение вектора
в пространстве и во времени представляется
в виде движения его конца по эллиптической
спирали (эллиптически поляризованная
волна). Шаг спирали равен длине волны
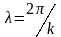 .
Если амплитуды
.
Если амплитуды
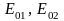 равны по величине, то волна будет
поляризована по кругу. Если одна из
амплитуд равна нулю, то волна линейно
поляризована. В общем случае плоская
монохроматическая волна поляризована
эллиптически.В силу того, что реальные
источники состоят из огромного числа
независимых излучателей, испускающих
волны со случайным распределением
амплитуд, начальных фаз и поляризаций,
реальные электромагнитные волны в целом
являются неполяризованными. Для получения
поляризованных волн необходимо, чтобы
элементарные источники были скоррелированы
друг с другом.
равны по величине, то волна будет
поляризована по кругу. Если одна из
амплитуд равна нулю, то волна линейно
поляризована. В общем случае плоская
монохроматическая волна поляризована
эллиптически.В силу того, что реальные
источники состоят из огромного числа
независимых излучателей, испускающих
волны со случайным распределением
амплитуд, начальных фаз и поляризаций,
реальные электромагнитные волны в целом
являются неполяризованными. Для получения
поляризованных волн необходимо, чтобы
элементарные источники были скоррелированы
друг с другом.
13 Интерференция — изменение в характере звуковых, тепловых, световых и электрических явлений, объясняемое колебательным движением: в первом случае частиц звучащего тела, в остальных трех — колебанием. Интерференция света — частный случай интерференции для видимой области электромагнитного спектра;
Явление интерференции происходит при взаимодействии двух и более волн одинаковой частоты, распространяющихся в различных направлениях. При этом оно наблюдается и у волн, распространяющихся в средах, и у электромагнитных волн. То есть интерференция является свойством волн как таковых и не зависит ни от свойств среды, ни от ее наличия.
Первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). Томас Юнг наблюдал интерференцию от двух источников, прокалывая на малом расстоянии (d ≈ 1мм) два маленьких отверстия в непрозрачном экране. Отверстия освещались светом от солнца, прошедшим через малое отверстие в другом непрозрачном экране. Давление в жидкости и газе Молекулы газа, совершая беспорядочное, хаотическое движение, не связаны или весьма слабо связаны силами взаимодействия, поэтому они движутся свободно и в результате соударений стремятся разлететься во все стороны, заполняя весь предоставленный им объем, т. е. объем газа определяется объемом того сосуда, который газ занимает.

Интерференционная картина наблюдалась на экране, удаленном на расстоянии L ≈ 1м от двух источников. Так, впервые в истории, Т. Юнг определил длины световых волн.При использовании лазера в качестве источника света необходимость в экране отпадает.
Утверждение о том, что волны от источников S1 и S2 распространяются независимо друг от друга, а в точке наблюдения они просто складываются, является опытным фактом и носит название принципа суперпозиции.
ИНТЕРФЕРЕНЦИОННАЯ КАРТИНА - регулярное чередование областей повыш. и пониж. интенсивности света, получающееся в результате наложения когерентных световых пучков, т. е. в условиях постоянной (или регулярно меняющейся) разности фаз между ними
Оптическая разность хода двух световых волн
Δ=L1—L2.
• Оптическая разность хода световых волн, отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластинки или пленки, находящейся в воздухе (рис. 30.1, а),
Δ=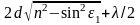 ,
или
,
или
Δ=2dn cos ε2’ + λ/2, где
d — толщина пластинки (пленки); ε1 — угол падения; ε2’ -— угол преломления.
• Связь разности фаз Δφ колебаний с оптической разностью хода волн
Δφ=2πΔ/λ..
• Условие максимумов интенсивности света при интерференции
Δ=±kλ (k=0,l,2,3, …).
• Условие минимумов интенсивности света при интерференции
Δ=±(2k+1) (λ/2).
Величина, равная произведению геометрической длины пути на абсолютный показатель преломления среды, называется оптической длиной пути.
14
Необходимым условием интерференции
волн является их когерентность, т. е.
согласованное протекание во времени и
пространстве нескольких колебательных
или волновых процессов. Этому условию
удовлетворяют монохроматические волны
— неограниченные в пространстве волны
одной определенной и строго постоянной
частоты. Так как ни один реальный источник
не дает строго монохроматического
света, то волны, излучаемые любыми
независимыми источниками света, всегда
некогерентны. Поэтому на опыте не
наблюдается интерференция света от
независимых источников, например от
двух электрических лампочек или от
разных точек нити накала одной
лампочки.Понять физическую причину
немонохроматичности, а следовательно,
и некогерентности волн, испускаемых
двумя независимыми источниками света,
можно исходя из самого механизма
испускания света атомами. В двух
самостоятельных источниках света атомы
излучают независимо друг от друга. В
каждом из таких атомов процесс излучения
конечен и длится очень короткое время
(![]() с).
За это время возбужденный атом возвращается
в нормальное состояние и излучение им
света прекращается. Возбудившись вновь,
атом снова начинает испускать световые
волны, но уже с новой начальной фазой.
Так как разность фаз между излучением
двух таких независимых атомов изменяется
при каждом новом акте испускания, то
волны, спонтанно излучаемые атомами
любого источника света, некогерентны.
Таким образом, волны, испускаемые
атомами, лишь в течение интервала
времени
с).
За это время возбужденный атом возвращается
в нормальное состояние и излучение им
света прекращается. Возбудившись вновь,
атом снова начинает испускать световые
волны, но уже с новой начальной фазой.
Так как разность фаз между излучением
двух таких независимых атомов изменяется
при каждом новом акте испускания, то
волны, спонтанно излучаемые атомами
любого источника света, некогерентны.
Таким образом, волны, испускаемые
атомами, лишь в течение интервала
времени ![]() с
имеют приблизительно постоянные
амплитуду и фазу колебаний, тогда как
за больший промежуток времени и амплитуда,
и фаза изменяются. Прерывистое излучение
света атомами в виде отдельных коротких
импульсов называется волновым цугом.
с
имеют приблизительно постоянные
амплитуду и фазу колебаний, тогда как
за больший промежуток времени и амплитуда,
и фаза изменяются. Прерывистое излучение
света атомами в виде отдельных коротких
импульсов называется волновым цугом.
(![]() 2.4.1)
2.4.1)
Принцип
суперпозиции есть
физическая гипотеза, согласно которой
для световых волн возмущение, создающееся
при прохождении ряда волн, равно
алгебраической сумме возмущений ,
производимых каждой волной в отдельности.
Уравнение (2.4.1) является математической
формулировкой этого принципа При
сложении колебаний можно пользоваться
аналитическим, графическим методами и
методом векторных диаграмм.Сложим
гармонические колебания одного
направления и одинаковой частоты:![]()
![]()
1. Аналитический метод. Результирующее смещение
![]()
Покажем, что результирующее колебание также является гармоническим колебанием той же частоты, т.е. что
![]()
где А —
амплитуда результирующего колебания; ![]() —
его начальная фаза. Тогда
—
его начальная фаза. Тогда
![]()
![]()
![]()
Решив эту систему уравнений, получим
![]()
![]()
2. Графический метод. Сложение сводится к суммированию ординат в каждый момент времени (чем больше точек, тем точнее) — рисунок 13.6.
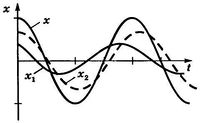
![]()
3. Метод векторных диаграмм.
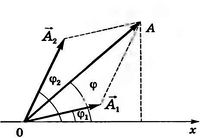
![]()
Вместо
разности фаз δφ интерферирующих волн
удобно ввести в рассмотрение
пропорциональную ей величину Δ —
оптическую разность хода, которая
отличается множителем λ/2π, где λ- длина
световой волны.
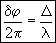
Изменению разности фаз на 2π соответствует изменение разности хода на λ. В вакууме оптическая разность хода в отличие от разности фаз имеет наглядную интерпретацию. Если две интерферирующие волны испускаются одним источником света, то разность хода — это геометрическая разность длин путей, по которым два интерферирующих луча от одной точки источника достигли одной точки экрана.В изотропной среде скорость света в n раз меньше, чем в вакууме, здесь n показатель преломления среды. Частота света в среде и в вакууме одинакова, поэтому длина волны в среде в n раз меньше. В соответствии соотношением вместо реального уменьшения длины волны λ можно рассматривать неизменную λ и соответствующее увеличение длины пути луча. С этой целью вводится понятие оптической длины пути, которая в n раз больше геометрической длины. Интенсивность интерференционной картины:
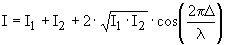


 ,
, 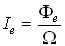 ,
,