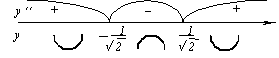- •Логарифмическая функция
- •Определение
- •[Править]Существование
- •Односторонний предел
- •3 Теоремы о пределах
- •Бесконечно малая величина
- •[Править]Бесконечно большая величина
- •Производная параметрически заданной функции
- •Четыре теоремы о дифференцируемых функциях
- •Достаточные условия убывания и возрастания функции. Достаточные условия экстремума функции.
Достаточные условия убывания и возрастания функции. Достаточные условия экстремума функции.
Теорема 1.Если функция f(x) имеет в каждой точке интервала (a, b) неотрицательную производную, то она является неубывающей функцией в этом интервале. Доказательство. Возьмем x1 < x2 из интервала (a, b). Для функции f(x) на интервале [x1 , x2] выполнены все условия теоремы Лагранжа. Поэтому
f(x2 ) - f(x1 ) = (x2 - x1 )f '(x0 ),
где x0 лежит в интервале (x1 , x2), а следовательно, и в интервале (a, b). По условию f '(x0 ) 0 и x2 > x1, следовательно,
f(x2 ) - f(x1 ) 0,
или
f(x2 ) f(x1 ) при x2 > x1 ,
что и требовалось доказать. Аналогично доказывается и другая теорема. Теорема 2. Если функция f(x) в каждой точке интервала (a, b) имеет неположительную производную, то она является невозрастающей функцией в этом интервале.
Пример 1.
Теорема 3. (первый достаточный признак экстремума). Если производная f '(x) функции f(x) обращается в нуль в точке x0 или не существует и при переходе через x0 меняет свой знак, то функция f(x) имеет в этой точке экстремум (максимум, если знак меняется с "+" на "-", и минимум, если знак меняется с "-" на "+"). Доказательство. Если производная f '(x) при переходе через x = x0 меняет знак с "+" на "-", то это означает, что при достаточно малом h производнаяf '(x) положительна в интервале (x0 - h, x0 ) и отрицательна в интервале (x0 , x0 + h). Следовательно, функция f(x) в интервале (x0 - h, x0 )возрастает, а в интервале (x0 , x0 + h) убывает, то есть в точке x0 достигает максимума. Аналогично доказывается утверждение данной теоремы относительно минимума функции. Заметим, что если производная f '(x), обращаясь в нуль в точке x0, не меняет знака, то в этой точке функция не имеет экстремума, так как с обеих сторон от точки x0 функция f(x) будет возрастать или убывать.
Пример 2. Пример 3.
Теорема
4. (второй
достаточный признак существования
экстремума функции). Если
в точке x0 первая
производная f '(x) функции f(x) обращается
в нуль, а её вторая производная f ''(x) отлична
от нуля, то в точке x0 функция f(x) достигает
экстремума (минимума, если f ''(x) > 0,
и максимума, еслиf ''(x) < 0).
Предполагается, что f ''(x) непрерывна
в точке x0 и
ее окрестности.
 Доказательство. Докажем
необходимость условия существования
максимума. Пустьf '(x) = 0, f ''(x) > 0.
Так
как f ''(x) непрерывна,
то в достаточно малом интервале (x0 - h,
x0 + h) вторая
производная положительна: f ''(x) > 0.
Это означает, что f '(x) возрастает
в этом интервале. Так как при этомf '(x0 )=0,
то f '(x)<0 в
интервале (x0 - h,
x0 ) и f '(x)>0 в
интервале (x0
, x0 + h).
Таким
образом, функция f(x) убывает
в интервале (x0 - h,
x0 ) и
возрастает в интервале (x0
, x0 + h).
Поэтому в точке x0 функция f(x) имеет
минимум. Аналогично доказывается
достаточность условия существования
максимума. На рисунке функция f(x) имеет
в точке x1 минимум,
в точке x2 -
максимум.
Второй производной
можно воспользоваться при решении задач
на отыскание максимума и минимума
функции.
Доказательство. Докажем
необходимость условия существования
максимума. Пустьf '(x) = 0, f ''(x) > 0.
Так
как f ''(x) непрерывна,
то в достаточно малом интервале (x0 - h,
x0 + h) вторая
производная положительна: f ''(x) > 0.
Это означает, что f '(x) возрастает
в этом интервале. Так как при этомf '(x0 )=0,
то f '(x)<0 в
интервале (x0 - h,
x0 ) и f '(x)>0 в
интервале (x0
, x0 + h).
Таким
образом, функция f(x) убывает
в интервале (x0 - h,
x0 ) и
возрастает в интервале (x0
, x0 + h).
Поэтому в точке x0 функция f(x) имеет
минимум. Аналогично доказывается
достаточность условия существования
максимума. На рисунке функция f(x) имеет
в точке x1 минимум,
в точке x2 -
максимум.
Второй производной
можно воспользоваться при решении задач
на отыскание максимума и минимума
функции.
17-18
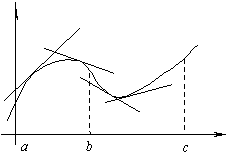
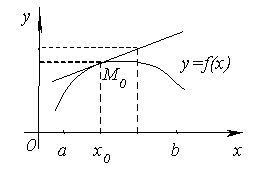
График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале. График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c). Примеры.
Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым. Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b)вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.
Доказательство. Предположим для определенности, что f''(x) < 0 и докажем, что график функции будет выпуклым. Возьмем
на графике функции y
= f(x) произвольную
точку M0 с
абсциссой x0 (a; b)
и проведем через точку M0 касательную.
Ее уравнение |
|
Итак,
уравнение кривой имеет вид y
= f(x).
Обозначим ![]() ординату
касательной, соответствующую абсциссе x.
Тогда
ординату
касательной, соответствующую абсциссе x.
Тогда ![]() .
Следовательно, разность ординат кривой
и касательной при одном и том же
значении x будет
.
Следовательно, разность ординат кривой
и касательной при одном и том же
значении x будет ![]() .
.
Разность f(x)
– f(x0) преобразуем
по теореме Лагранжа ![]() ,
где c между x и x0.
,
где c между x и x0.
Таким образом,
![]() .
.
К
выражению, стоящему в квадратных скобках
снова применим теорему Лагранжа: ![]() ,
где c1 между c0 иx0.
По условию теоремы f ''(x)
< 0. Определим знак произведения второго
и третьего сомножителей.
,
где c1 между c0 иx0.
По условию теоремы f ''(x)
< 0. Определим знак произведения второго
и третьего сомножителей.
Предположим, что x>x0. Тогда x0<c1<c<x, следовательно,
 (x
– x0)
> 0 и (c
– x0)
> 0. Поэтому
(x
– x0)
> 0 и (c
– x0)
> 0. Поэтому 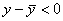 .
.Пусть x<x0, следовательно, x < c < c1 < x0 и (x – x0) < 0, (c – x0) < 0. Поэтому вновь .
Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x0 (a; b), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично.
Примеры.
Установить интервалы выпуклости и вогнутости кривой y = 2 – x2.
Найдем y '' и определим, где вторая производная положительна и где отрицательна. y' = –2x, y'' = –2 < 0 на (–∞; +∞), следовательно, функция всюду выпукла.
y = ex. Так как y'' = ex > 0 при любых x, то кривая всюду вогнута.



y = x3. Так как y'' = 6x, то y'' < 0 при x < 0 и y'' > 0 при x > 0. Следовательно, при x < 0 кривая выпукла, а при x > 0 вогнута.
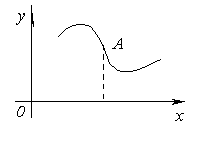
Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба. Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею. Определим достаточные условия того, что данная точка кривой является точкой перегиба. Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба. Доказательство. Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0. Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует. Примеры. Найти точки перегиба и определить интервалы выпуклости и вогнутости кривых. Найдем производные заданной функции до второго порядка.
Итак, точка перегиба x = 1. Функция выпукла на (1; +∞), вогнута на (–∞; 1).
Возможные
точки перегиба найдем, решив уравнение
2x2 –
1 = 0. Отсюда
Точки
перегиба
Следовательно, f(x) выпуклая на (–1; 1). |
|
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
При исследовании функции важно установить форму ее графика при неограниченном удалении точки графика от начала координат.
Особый интерес представляет случай, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.
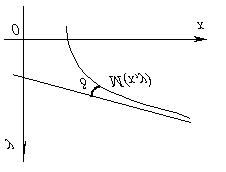
 Прямая
называется асимптотой графика
функции y = f(x),
если расстояние от переменной
точки M графика
до этой прямой при удалении точки M в
бесконечность стремится к нулю, т.е.
точка графика функции при своем стремлении
в бесконечность должна неограниченно
приближаться к асимптоте.
Прямая
называется асимптотой графика
функции y = f(x),
если расстояние от переменной
точки M графика
до этой прямой при удалении точки M в
бесконечность стремится к нулю, т.е.
точка графика функции при своем стремлении
в бесконечность должна неограниченно
приближаться к асимптоте.
Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.
Если обозначим через d расстояние от точки M кривой до асимптоты, то ясно, что d стремится к нулю при удалении точки M в бесконечность.
Будем в дальнейшем различать асимптоты вертикальные и наклонные.
ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ
Пусть
при x→ x0 с
какой-либо стороны функция y = f(x)неограниченно
возрастает по абсолютной величине,
т.е. ![]() или
или![]() или
или ![]() .
Тогда из определения асимптоты следует,
что прямая x = x0 является
асимптотой. Очевидно и обратное, если
прямая x = x0 является
асимптотой, т. о.
.
.
Тогда из определения асимптоты следует,
что прямая x = x0 является
асимптотой. Очевидно и обратное, если
прямая x = x0 является
асимптотой, т. о.
.
Т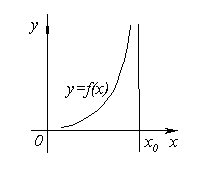 аким
образом, вертикальной асимптотой графика
функции y
= f(x) называется
прямая, еслиf(x) →
∞ хотя бы при одном из условий x→ x0 –
0 или x → x0 +
0, x = x0
аким
образом, вертикальной асимптотой графика
функции y
= f(x) называется
прямая, еслиf(x) →
∞ хотя бы при одном из условий x→ x0 –
0 или x → x0 +
0, x = x0
Следовательно, для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x0, при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение x = x0.
Примеры.
Найти вертикальные асимптоты графика функции
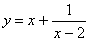 .
.
Так
как ![]() ,
то прямая x =
2 является вертикальной асимптотой.
,
то прямая x =
2 является вертикальной асимптотой.
 .
.
Прямая x = 0 – вертикальная асимптота.
НАКЛОННЫЕ АСИМПТОТЫ
Поскольку асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту, то ее уравнение будет y = kx + b. Наша задача найти коэффициенты k и b.
Т еорема.
Прямая y = kx + b служит
наклонной асимптотой при x →
+∞ для графика функции y= f(x) тогда
и только тогда, когда
еорема.
Прямая y = kx + b служит
наклонной асимптотой при x →
+∞ для графика функции y= f(x) тогда
и только тогда, когда ![]() .
Аналогичное утверждение верно и при x →
–∞.
.
Аналогичное утверждение верно и при x →
–∞.
Доказательство.
Пусть MP –
длина отрезка, равного расстоянию от
точки M до
асимптоты. По условию ![]() .
Обозначим через φ угол наклона асимптоты
к оси Ox.
Тогда из ΔMNPследует,
что
.
Обозначим через φ угол наклона асимптоты
к оси Ox.
Тогда из ΔMNPследует,
что ![]() .
Так как φ постоянный угол (φ ≠ π/2), то
.
Так как φ постоянный угол (φ ≠ π/2), то ![]() ,
но
,
но
MN = MK – NK = y - yас = f(x) - (kx+b).
Следовательно,
мы можем записать следующее равенство ![]() .
.
Так
как x →
+∞, то должно выполняться равенство ![]() .
Но при постоянных k и b
.
Но при постоянных k и b ![]() и
и ![]() .
Следовательно,
.
Следовательно, ![]() ,
т.е.
,
т.е. ![]() .
.
Если
число k уже
известно, то ![]() ,
поэтому
,
поэтому ![]() .
.
Для доказательства в случае x → –∞ все рассуждения аналогичны.
Докажем
обратное утверждение. Предположим, что
существуют пределы, определяющие
числа k и b.
Тогда несложно заметить, что выполняется
равенство ![]() .
Действительно
.
Действительно

Следовательно, прямая y = kx + b есть асимптота. Теорема полностью доказана.
Сделаем несколько замечаний.
Замечание 1. Теорема показывает, что для нахождения асимптот достаточно найти два указанных предела. Причем, если хотя бы один из пределов не существует или обращается в бесконечность, то кривая асимптот не имеет.
Замечание 2. В случае, когда k = 0 асимптота y = b называется горизонтальной асимптотой. Наличие горизонтальной асимптоты означает, что существуют пределы
![]() .
.
Замечание 3. Пределы для отыскания k и b могут быть различны при x → +∞ и x → – ∞ и, следовательно, график функции может иметь две различные асимптоты при x → +∞ и x → –∞.
Примеры. Найти асимптоты кривых.
 .
.Вертикальные:
![]()
x = 0 – вертикальная асимптота.
Наклонные:
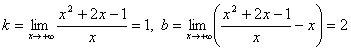 .
.
При x → - ∞ получим те же значения k и b. Следовательно, прямая y = x + 2 является наклонной асимптотой.
y = e–x sin x + x.
Функция определена и непрерывна на всей числовой прямой, следовательно, вертикальных асимптот нет.
а) 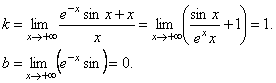 .
.
Итак, при x → +∞ наклонная асимптота у= х.
б)  ,
т. к.
,
т. к.
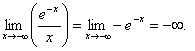 ,
поэтому при x →
- ∞ наклонных асимптот нет.
,
поэтому при x →
- ∞ наклонных асимптот нет.
y = x – 2arctg x.
Вертикальных асимптот нет.
а) ![]() .
.
![]() .
Наклонная асимптота y = x – π при
.
Наклонная асимптота y = x – π при ![]() .
.
б) ![]() при
при ![]() .
.
(19) 23
Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
 нормаль
нормаль
касательная плоскость
Пусть N и N0 – точки данной поверхности. Проведем прямую NN0. Плоскость, которая проходит через точку N0, называется касательной плоскостью к поверхности, если угол между секущейNN0 и этой плоскостью стремится к нулю, когда стремится к нулю расстояние NN0. Поверхностный интеграл Примеры решения и оформления задач контрольной работы
Определение. Нормалью к поверхности в точке N0 называется прямая, проходящая через точку N0 перпендикулярно касательной плоскости к этой поверхности.
В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.
Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М0(х0, у0), касательная плоскость в точке N0(x0,y0,(x0,y0)) существует и имеет уравнение:
![]() .
.
Примеры выполнения курсовой работы Электротехника
Уравнение нормали к поверхности в этой точке:
![]()
Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х0, у0) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х0, у0) к точке (х0+х, у0+у).
Как видно, геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.
Пример. Найти уравнения касательной плоскости и нормали к поверхности
![]()
в точке М(1, 1, 1).
![]()
![]()
Уравнение касательной плоскости:
![]()
Уравнение нормали:
![]()
Приближенные вычисления с помощью полного дифференциала.
Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное приращение этой функции:
![]()
![]()
Если подставить в эту формулу выражение
![]()
то получим приближенную формулу:
![]()
Пример. Вычислить
приближенно значение ![]() ,
исходя из значения функции
,
исходя из значения функции ![]() при x =
1, y =
2, z =
1.
при x =
1, y =
2, z =
1.
[an error occurred while processing this directive]
Из заданного выражения определим x = 1,04 – 1 = 0,04, y = 1,99 – 2 = -0,01,
z = 1,02 – 1 = 0,02.
Найдем значение
функции u(x, y, z)
= ![]()
Находим частные производные:
![]()
![]()

Полный дифференциал функции u равен:
![]()
![]()
Точное значение этого выражения: 1,049275225687319176.

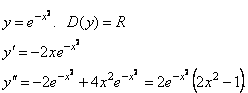
 при
всех x из
(–1; 1).
при
всех x из
(–1; 1).