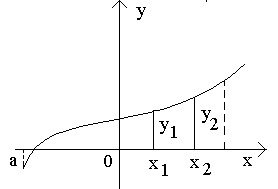- •Логарифмическая функция
- •Определение
- •[Править]Существование
- •Односторонний предел
- •3 Теоремы о пределах
- •Бесконечно малая величина
- •[Править]Бесконечно большая величина
- •Производная параметрически заданной функции
- •Четыре теоремы о дифференцируемых функциях
- •Достаточные условия убывания и возрастания функции. Достаточные условия экстремума функции.
Бесконечно малая величина
Последовательность an называется бесконечно
малой,
если ![]() .
Например, последовательность чисел
.
Например, последовательность чисел ![]() —
бесконечно малая.
—
бесконечно малая.
Функция
называется бесконечно
малой в окрестности точки x0,
если ![]() .
.
Функция
называется бесконечно
малой на бесконечности,
если ![]() либо
либо ![]() .
.
Также
бесконечно малой является функция,
представляющая собой разность функции
и её предела, то есть если ![]() ,
то f(x)
− a =
α(x),
,
то f(x)
− a =
α(x), ![]() .
.
[Править]Бесконечно большая величина
Во
всех приведённых ниже формулах
бесконечность справа от равенства
подразумевается определённого знака
(либо «плюс», либо «минус»). То есть,
например, функция xsin x,
неограниченная с обеих сторон, не
является бесконечно большой при ![]() .
.
Последовательность an называется бесконечно
большой,
если ![]() .
.
Функция
называется бесконечно
большой в окрестности точки x0,
если ![]() .
.
Функция
называется бесконечно
большой на бесконечности,
если ![]() либо
либо ![]() .
.
[Функция y=f(x) называется бесконечно
малой при x→a или
при x→∞,
если ![]() или
или ![]() ,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю.
,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю.
П римеры.
римеры.
Функция f(x)=(x-1)2 является бесконечно малой при x→1, так как
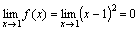 (см.
рис.).
(см.
рис.).Функция f(x) = tgx – бесконечно малая при x→0.
f(x) = ln (1+x)– бесконечно малая при x→0.
f(x) = 1/x– бесконечно малая при x→∞.
Установим следующее важное соотношение:
Теорема. Если
функция y=f(x) представима
при x→aв
виде суммы постоянного числа b и
бесконечно малой величины α(x):
f (x)=b+ α(x) то ![]() .
.
Обратно, если , то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.
Доказательство.
Докажем первую часть утверждения. Из равенства f(x)=b+α(x) следует |f(x) – b|=| α|. Но так как a(x) – бесконечно малая, то при произвольном ε найдется δ – окрестность точки a, при всех x из которой, значения a(x) удовлетворяют соотношению|α(x)|<ε. Тогда |f(x) – b|< ε. А это и значит, что .
Если , то при любом ε>0 для всех х из некоторой δ – окрестность точки a будет |f(x) – b|< ε. Но если обозначимf(x) – b= α, то |α(x)|<ε, а это значит, что a – бесконечно малая.
Рассмотрим основные свойства бесконечно малых функций.
Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.
Доказательство.
Приведем доказательство для двух
слагаемых. Пусть f(x)=α(x)+β(x),
где ![]() и
и ![]() .
Нам нужно доказать, что при произвольном
как угодно малом ε>0
найдется δ>0,
такое, что для x,
удовлетворяющих неравенству |x
– a|<δ,
выполняется |f(x)|< ε.
.
Нам нужно доказать, что при произвольном
как угодно малом ε>0
найдется δ>0,
такое, что для x,
удовлетворяющих неравенству |x
– a|<δ,
выполняется |f(x)|< ε.
Итак, зафиксируем произвольное число ε>0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ1>0, что при |x – a|<δ1 имеем |α(x)|< ε/2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ2>0, что при |x – a|<δ2 имеем | β(x)|< ε/2.
Возьмем δ=min{ δ1, δ2}.Тогда в окрестности точки a радиуса δбудет выполняться каждое из неравенств |α(x)|< ε/2 и | β(x)|<ε/2. Следовательно, в этой окрестности будет
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)| < ε/2 + ε/2= ε,
т.е. |f(x)|<ε, что и требовалось доказать.
Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.
Доказательство. Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε>0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих окрестностей имеем | αf|<ε/M= ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.
Из доказанной теоремы вытекают:
Следствие
1. Если
и
,
то ![]() .
.
Следствие
2. Если
и c=const,
то ![]() .
.
Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.
Доказательство.
Пусть ![]() .
Тогда 1/f(x) есть
ограниченная функция. Поэтому дробь
.
Тогда 1/f(x) есть
ограниченная функция. Поэтому дробь ![]() есть
произведение бесконечно малой функции
на функцию ограниченную, т.е. функция
бесконечно малая.
есть
произведение бесконечно малой функции
на функцию ограниченную, т.е. функция
бесконечно малая.
СООТНОШЕНИЕ МЕЖДУ БЕСКОНЕЧНО МАЛЫМИ
И БЕСКОНЕЧНО БОЛЬШИМИ ФУНКЦИЯМИ
Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a.
Доказательство. Возьмем
произвольное число ε>0 и
покажем, что при некотором δ>0 (зависящим
от ε) при всех x,
для которых|x
– a|<δ,
выполняется неравенство ![]() ,
а это и будет означать, что 1/f(x) –
бесконечно малая функция. Действительно,
так как f(x) –
бесконечно большая функция при x→a,
то найдется δ>0 такое,
что как только |x
– a|<δ,
так |f(x)|>1/ ε.
Но тогда для тех же x
.
,
а это и будет означать, что 1/f(x) –
бесконечно малая функция. Действительно,
так как f(x) –
бесконечно большая функция при x→a,
то найдется δ>0 такое,
что как только |x
– a|<δ,
так |f(x)|>1/ ε.
Но тогда для тех же x
.
Примеры.
Ясно, что при x→+∞ функция y=x2+1 является бесконечно большой. Но тогда согласно сформулированной выше теореме функция
 –
бесконечно малая при x→+∞,
т.е.
–
бесконечно малая при x→+∞,
т.е. 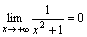 .
.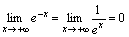 .
.
Можно доказать и обратную теорему.
Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x) является бесконечно большой функцией.
Доказательство теоремы проведите самостоятельно.
Примеры.
 .
. .
.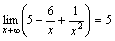 ,
так как функции
,
так как функции 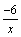 и
и 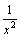 -
бесконечно малые при x→+∞,
то
-
бесконечно малые при x→+∞,
то 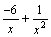 ,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же
,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же  является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0
![]()
4
НЕПРЕРЫВНЫЕ ФУНКЦИИ НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ
П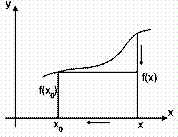 редставление
о непрерывности функции интуитивно
связано у нас с тем, что её графиком
является плавная, нигде не прерывающаяся
линия. При рассмотрении графика такой
функции y
= f(x) мы
видим, что близким значениям аргумента
соответствуют близкие значения функции:
если независимая переменная
редставление
о непрерывности функции интуитивно
связано у нас с тем, что её графиком
является плавная, нигде не прерывающаяся
линия. При рассмотрении графика такой
функции y
= f(x) мы
видим, что близким значениям аргумента
соответствуют близкие значения функции:
если независимая переменная ![]() приближается
к точке x0,
то значение функции y
= f(x) неограниченно
приближается к значению функции в
точкеx0,
т.е. к f(x0).
приближается
к точке x0,
то значение функции y
= f(x) неограниченно
приближается к значению функции в
точкеx0,
т.е. к f(x0).
Дадим строгое определение непрерывности функции. Итак, пусть имеем функцию y = f(x).
Функция y = f(x) называется непрерывной в точке x0, если она определена в этой точке и в некоторой окрестности содержащей x0 и
|
(1) |
Таким образом, можно сказать, что функция непрерывна в точкеx0, если выполнены 3 условия:
она определена в точке x0 и в некоторой её окрестности;
имеет предел при x → x0;
этот предел равен значению функции в точке x0.
Формулу
(1) можно записать в виде ![]() ,
т.к.
,
т.к. ![]() .
Это означает, что для того, чтобы найти
предел непрерывной функции при x
→
x0,
достаточно в выражение функции подставить
вместо аргумента xего
значение x0.
.
Это означает, что для того, чтобы найти
предел непрерывной функции при x
→
x0,
достаточно в выражение функции подставить
вместо аргумента xего
значение x0.
Пример: Докажем,
что функция y =
3x2 непрерывна
в произвольной точке x0.
Для этого найдем ![]() .
.
Если функция y=f(x) непрерывна в каждой точке некоторого интервала (a; b), где a < b, то говорят, что функция непрерывна на этом интервале.
Непрерывные функции обладают следующими свойствами.
Теорема 1. Если функции f(x) и g(x) непрерывны в точке x0, то их сумма φ(x) = f(x) + g(x) также есть непрерывная функция в точке x0.
Доказательство.
Так как функции f(x) и g(x) непрерывны
в точке x0,
то исходя из определения можно написать ![]() .
Тогда на основании свойств пределов
будем иметь
.
Тогда на основании свойств пределов
будем иметь
![]() .
.
Эта теорема справедлива для любого конечного числа слагаемых.
Следующие две теоремы докажите самостоятельно аналогично теореме 1.
Теорема 2. Произведение двух непрерывных функций есть функция непрерывная.
Теорема 3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.
Если
функцию можно представить в виде y
= f(u),
где u
= φ(x),
т.е. если функция ![]() зависит
от переменной
через
промежуточный аргумент u,
то
называется сложной
функцией переменной x.
зависит
от переменной
через
промежуточный аргумент u,
то
называется сложной
функцией переменной x.
Примеры:
y = sinx3. Здесь u = x3, y = sin u.
y = etg x, u = tg x, y = eu.
Таким образом, под термином сложная функция следует понимать не какое – либо очень сложное выражение, а функцию, которая зависит от аргумента x через несколько промежуточных функций.
Справедлива следующая теорема.
Теорема 4. Если функция u = φ(x) непрерывна в точкеx0 и принимает в этой точке значение u0 = φ(x0), а функция f(u)непрерывна в точке u0, то сложная функция y = f(φ(x)) непрерывна в точке x0.
Используя эти теоремы можно доказать следующий результат.
Теорема 5. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Заметим, что если функция y = f(x) непрерывна в точке x0 и её значение в этой точке отлично от 0, f(x0) ≠ 0, то значения функции f(x) в некоторой окрестности точки x0 имеют тот же знак, что и f(x0), т.е. если f(x0) > 0, то найдётся такое δ > 0, что на интервале(x0– δ;x0+ δ) f(x) > 0 (в этой окрестности значения функции f(x) очень мало отличаются от своего предела).
5I. ![]() .
.
Доказательство см. в курсе 10 класса.
II. ![]() .
.
Доказательство.
![]()
Из
непрерывности функции ![]() получаем
требуемое (
получаем
требуемое (![]() ).
).
III. ![]() .
.
Доказательство. Положим ![]() .
.
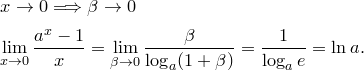
Если ![]() ,
то
,
то ![]() .
.
Если ![]() ,
то
,
то
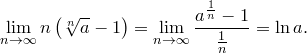
IV. ![]() .
.
Доказательство.
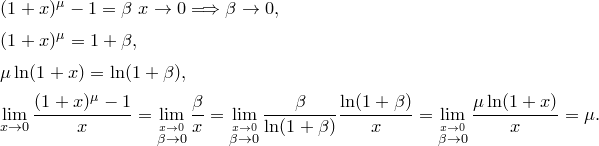
V. ![]() .
.
Доказательство.
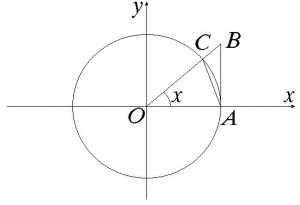
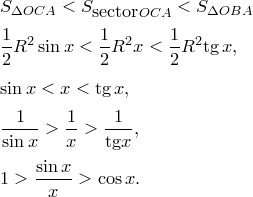
При ![]()
![]() по
теореме о двух милиционерах.
по
теореме о двух милиционерах.
Таким
образом, ![]() .
.
Пусть ![]() , тогда
, тогда ![]() .
.
 Значит,
.
Значит,
.
7
СООТНОШЕНИЕ МЕЖДУ БЕСКОНЕЧНО МАЛЫМИ
И БЕСКОНЕЧНО БОЛЬШИМИ ФУНКЦИЯМИ
Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a.
Доказательство. Возьмем произвольное число ε>0 и покажем, что при некотором δ>0 (зависящим от ε) при всех x, для которых|x – a|<δ, выполняется неравенство , а это и будет означать, что 1/f(x) – бесконечно малая функция. Действительно, так как f(x) – бесконечно большая функция при x→a, то найдется δ>0 такое, что как только |x – a|<δ, так |f(x)|>1/ ε. Но тогда для тех же x .
Примеры.
Ясно, что при x→+∞ функция y=x2+1 является бесконечно большой. Но тогда согласно сформулированной выше теореме функция – бесконечно малая при x→+∞, т.е. .
.
Можно доказать и обратную теорему.
Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x) является бесконечно большой функцией.
Доказательство теоремы проведите самостоятельно.
Примеры.
.
.
, так как функции и - бесконечно малые при x→+∞, то , как сумма бесконечно малых функций есть функция бесконечно малая. Функция же является суммой постоянного числа и бесконечно малой функции. Следовательно, по теореме 1 для бесконечно малых функций получаем нужное равенство.
Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0
.
СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ
Пусть при x→a функции f(x) и g(x) являются бесконечно малыми. Тогда будем пользоваться следующими определениями.
Если
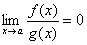 ,
то f(x) называется бесконечно
малой высшего порядка,
чем g(x) (относительно g(x)).
,
то f(x) называется бесконечно
малой высшего порядка,
чем g(x) (относительно g(x)).Если
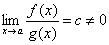 ,
то функции f(x) и g(x) называются бесконечно
малыми одногопорядка.
,
то функции f(x) и g(x) называются бесконечно
малыми одногопорядка.Если
 ,
то f(x) называется бесконечно
малой k-го порядка относительноg(x).
,
то f(x) называется бесконечно
малой k-го порядка относительноg(x).
Если ![]() ,
то функции f(x) и g(x) называются эквивалентными
бесконечно малыми.
В этом случае обе функции стремятся к
нулю примерно с одинаковой скоростью.
Эквивалентные бесконечно малые будем
обозначать f
≈ g.
,
то функции f(x) и g(x) называются эквивалентными
бесконечно малыми.
В этом случае обе функции стремятся к
нулю примерно с одинаковой скоростью.
Эквивалентные бесконечно малые будем
обозначать f
≈ g.
Примеры.
Пусть f(x)=x2,g(x)=5x. Функции являются бесконечно малыми при x→0. Найдем
 .
Следовательно, f(x) –
бесконечно малая высшего порядка
относительно g(x).
.
Следовательно, f(x) –
бесконечно малая высшего порядка
относительно g(x).Пусть f(x)=x2–4,g(x)=x2–5x+6 – бесконечно малые при x→2.
![]() .
.
Поэтому f(x) и g(x) одного порядка.
f(x)=tg2x,g(x) = 2x – бесконечно малые при х→0.
![]() .
.
Следовательно, f ≈ g.
 –
бесконечно
малые при n→∞.
–
бесконечно
малые при n→∞.
![]() –
этот
предел не существует. Поэтому говорят,
что функции f и g не
сравнимы.
–
этот
предел не существует. Поэтому говорят,
что функции f и g не
сравнимы.
При вычислении пределов полезно помнить о следующем свойстве эквивалентных бесконечно малых функций.
Теорема. Пусть f и g –
бесконечно малые функции при х→а.
Если ![]() и f
≈ f1, g ≈ g1,
то
и f
≈ f1, g ≈ g1,
то ![]() ,
т.е. если отношение двух бесконечно
малых имеет предел, то этот предел не
изменится, если каждую из бесконечно
малых заменить эквивалентной бесконечно
малой.
,
т.е. если отношение двух бесконечно
малых имеет предел, то этот предел не
изменится, если каждую из бесконечно
малых заменить эквивалентной бесконечно
малой.
Доказательство.
Имеем ![]() .
Тогда
.
Тогда
![]() ,
,
что и требовалось доказать.
Докажите самостоятельно эквивалентность следующих бесконечно малых функций при
x→0: sinx ≈ x,tgx ≈ x,arcsinx ≈ x,arctgx ≈ x,1–cosx ≈ x2∕2,loga(1+x) ≈ x/lna,ln (1+x) ≈ x,(1+x)m–1 ≈ mx,ax–1 ≈ xlna,ex–1 ≈ x.
Примеры.
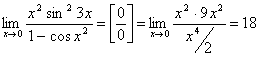 .
.
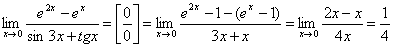 .
.
8
ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ
ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
Пусть имеем некоторую функцию y=f(x), определенную на некотором промежутке. Для каждого значения аргумента xиз этого промежутка функция y=f(x) имеет определенное значение.
Рассмотрим
два значения аргумента: исходное x0 и
новое x. 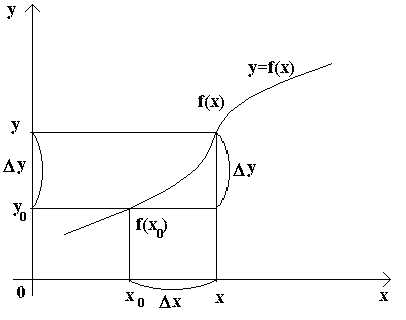 Разностьx–
x0 называется приращением
аргумента x в
точке x0 и
обозначается Δx.
Таким образом, Δx
= x – x0 (приращение
аргумента может быть как положительным,
так и отрицательным). Из этого равенства
следует, что x=x0+Δx,
т.е. первоначальное значение переменной
получило некоторое приращение. Тогда,
если в точке x0 значение
функции было f(x0), то
в новой точке x функция
будет принимать значение f(x)
= f(x0 +Δx).
Разностьx–
x0 называется приращением
аргумента x в
точке x0 и
обозначается Δx.
Таким образом, Δx
= x – x0 (приращение
аргумента может быть как положительным,
так и отрицательным). Из этого равенства
следует, что x=x0+Δx,
т.е. первоначальное значение переменной
получило некоторое приращение. Тогда,
если в точке x0 значение
функции было f(x0), то
в новой точке x функция
будет принимать значение f(x)
= f(x0 +Δx).
Разность y – y0 = f(x) – f(x0) называется приращением функции y = f(x) в точке x0 и обозначается символом Δy. Таким образом,
Δy = f(x) – f(x0) = f(x0 +Δx) - f(x0). |
(1) |
Обычно исходное значение аргумента x0 считается фиксированным, а новое значение x – переменным. Тогда y0 = f(x0)оказывается постоянной, а y = f(x) – переменной. Приращения Δy и Δxтакже будут переменными и формула (1) показывает, чтоDy является функцией переменной Δx.
Составим отношение приращения функции к приращению аргумента
![]()
Найдем предел этого отношения при Δx→0. Если этот предел существует, то его называют производной данной функции f(x) в точке x0 и обозначают f '(x0). Итак,
![]() .
.
Производной данной функции y = f(x) в точке x0 называется предел отношения приращения функции Δy к приращению аргумента Δx, когда последнее произвольным образом стремится к нулю.
Заметим, что для одной и той же функции производная в различных точках xможет принимать различные значения, т.е. производную можно рассматривать как функцию аргумента x. Эта функция обозначается f '(x)
Производная
обозначается символами f '(x),y ', ![]() .
Конкретное значение производной при x
= aобозначается f '(a)
или y '|x=a.
.
Конкретное значение производной при x
= aобозначается f '(a)
или y '|x=a.
Операция нахождения производной от функции f(x) называется дифференцированием этой функции.
Для непосредственного нахождения производной по определению можно применить следующее практическое правило:
Придать x приращение Δx и найти наращенное значение функции f(x + Δx).
Найти приращение функции Δy = f(x + Δx) – f(x).
Составить отношение
 и
найти предел этого отношения при Δx∞0.
и
найти предел этого отношения при Δx∞0.
Примеры.
Найти производную функции y = x2
а) в произвольной точке;
б) в точке x= 2.
а)
f(x + Δx) = (x + Δx)2;
Δy = (x + Δx)2 – x2=2xΔx– x2;
 .
.
б) f '(2) = 4
Используя определение найти производную функции
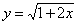 в
произвольной точке.
в
произвольной точке.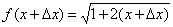 .
.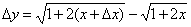
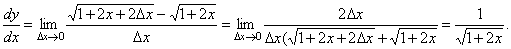
МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Из физики известно, что закон равномерного движения имеет вид s = v·t, где s – путь, пройденный к моменту времени t, v– скорость равномерного движения.
Однако, т.к. большинство движений происходящих в природе, неравномерно, то в общем случае скорость, а, следовательно, и расстояние sбудет зависеть от времени t, т.е. будет функцией времени.
Итак, пусть материальная точка движется по прямой в одном направлении по закону s=s(t).
Отметим некоторый момент времени t0. К этому моменту точка прошла путь s=s(t0). Определим скорость vматериальной точки в момент времени t0.
Для этого рассмотрим какой-нибудь другой момент времени t0+Δt. Ему соответствует пройденный путь s=s(t0+Δt). Тогда за промежуток времени Δt точка прошла путь Δs=s(t0+Δt)–s(t).
Рассмотрим
отношение ![]() .
Оно называется средней скоростью в
промежутке времени Δt.
Средняя скорость не может точно
охарактеризовать быстроту перемещения
точки в момент t0 (т.к.
движение неравномерно). Для того, чтобы
точнее выразить эту истинную скорость
с помощью средней скорости, нужно взять
меньший промежуток времени Δt.
.
Оно называется средней скоростью в
промежутке времени Δt.
Средняя скорость не может точно
охарактеризовать быстроту перемещения
точки в момент t0 (т.к.
движение неравномерно). Для того, чтобы
точнее выразить эту истинную скорость
с помощью средней скорости, нужно взять
меньший промежуток времени Δt.
Итак, скоростью движения в данный момент времени t0 (мгновенной скоростью) называется предел средней скорости в промежутке от t0 до t0+Δt, когда Δt→0:
![]() ,
,
т.е. скорость неравномерного движения это производная от пройденного пути по времени.
Г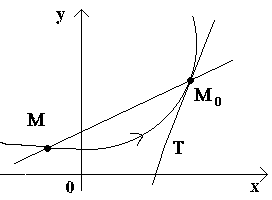 ЕОМЕТРИЧЕСКИЙ
СМЫСЛ ПРОИЗВОДНОЙ
ЕОМЕТРИЧЕСКИЙ
СМЫСЛ ПРОИЗВОДНОЙ
Введем сначала определение касательной к кривой в данной точке.
Пусть имеем кривую и на ней фиксированную точку М0 (см. рисунок).Рассмотрим другую точку М этой кривой и проведем секущую M0M. Если точка М начинает перемещаться по кривой, а точка М0 остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М0 с любой стороны секущая стремится занять положение определенной прямой М0Т, то прямая М0Т называется касательной к кривой в данной точке М0.
Т.о., касательной к кривой в данной точке М0 называется предельное положение секущей М0М, когда точка М стремится вдоль кривой к точке М0.
Р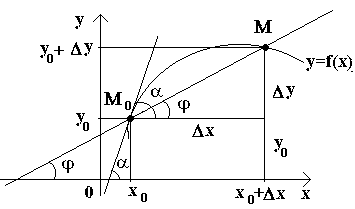 ассмотрим
теперь непрерывную функцию y=f(x) и
соответствующую этой функции кривую.
При некотором значении х0 функция
принимает значениеy0=f(x0). Этим
значениям x0 и y0 на
кривой соответствует точка М0(x0;
y0).Дадим
аргументу x0 приращение
Δх.
Новому значению аргумента соответствует
наращенное значение функции y0+Δ y=f(x0–Δx).
Получаем точку М(x0+Δx; y0+Δy). Проведем
секущую М0М и
обозначим через φ угол, образованный
секущей с положительным направлением
оси Ox.
Составим отношение
ассмотрим
теперь непрерывную функцию y=f(x) и
соответствующую этой функции кривую.
При некотором значении х0 функция
принимает значениеy0=f(x0). Этим
значениям x0 и y0 на
кривой соответствует точка М0(x0;
y0).Дадим
аргументу x0 приращение
Δх.
Новому значению аргумента соответствует
наращенное значение функции y0+Δ y=f(x0–Δx).
Получаем точку М(x0+Δx; y0+Δy). Проведем
секущую М0М и
обозначим через φ угол, образованный
секущей с положительным направлением
оси Ox.
Составим отношение ![]() и
заметим, что
и
заметим, что ![]() .
.
Если теперь Δx→0, то в силу непрерывности функции Δу→0, и поэтому точка М, перемещаясь по кривой, неограниченно приближается к точке М0. Тогда секущая М0М будет стремиться занять положение касательной к кривой в точке М0, а угол φ→α при Δx→0, где через α обозначили угол между касательной и положительным направлением оси Ox. Поскольку функция tg φ непрерывно зависит от φ при φ≠π/2 то при φ→α tg φ → tg α и, следовательно, угловой коэффициент касательной будет:
![]()
т.е. f '(x) = tg α .
Т.о., геометрически у '(x0) представляет угловой коэффициент касательной к графику этой функции в точке x0, т.е. при данном значении аргумента x, производная равна тангенсуугла, образованного касательной к графику функции f(x) в соответствующей точке М0 (x; y) с положительным направлением оси Ox.
Пример. Найти угловой коэффициент касательной к кривой у = х2 в точке М(-1; 1).
Ранее мы уже видели, что (x2)' = 2х. Но угловой коэффициент касательной к кривой есть tg α = y'|x=-1 = – 2.
9ТЕОРЕМА О ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ
Пусть y = f(u), а u= u(x). Получаем функцию y, зависящую от аргумента x: y = f(u(x)). Последняя функция называется функцией от функции или сложной функцией.
Областью определения функции y = f(u(x)) является либо вся область определения функции u=u(x) либо та ее часть, в которой определяются значения u, не выходящие из области определения функции y= f(u).
Операция "функция от функции" может проводиться не один раз, а любое число раз.
Установим правило дифференцирования сложной функции.
Теорема. Если
функция u= u(x)
имеет в некоторой точке x0 производную ![]() и
принимает в этой точке значение u0 =u(x0),
а функция y=
f(u) имеет
в точке u0 производную y 'u= f '(u0),
то сложная функция y
= f(u(x)) в
указанной точке x0 тоже
имеет производную, которая
равна y 'x= f '(u0)·u '(x0),
где вместо u должно
быть подставлено выражение u= u(x).
и
принимает в этой точке значение u0 =u(x0),
а функция y=
f(u) имеет
в точке u0 производную y 'u= f '(u0),
то сложная функция y
= f(u(x)) в
указанной точке x0 тоже
имеет производную, которая
равна y 'x= f '(u0)·u '(x0),
где вместо u должно
быть подставлено выражение u= u(x).
Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументуu на производную промежуточного аргумента по x.
Доказательство. При фиксированном значении х0 будем иметь u0=u(x0), у0=f(u0). Для нового значения аргумента x0+Δx:
Δu= u(x0 + Δx) – u(x0), Δy=f(u0+Δu) – f(u0).
Т.к. u – дифференцируема в точке x0, то u – непрерывна в этой точке. Поэтому при Δx→0 Δu→0. Аналогично при Δu→0 Δy→0.
По
условию ![]() .
Из этого соотношения, пользуясь
определением предела, получаем (при
Δu→0)
.
Из этого соотношения, пользуясь
определением предела, получаем (при
Δu→0)
![]() ,
,
где α→0 при Δu→0, а, следовательно, и при Δx→0.
Перепишем это равенство в виде:
Δy= y 'uΔu+α·Δu.
Полученное равенство справедливо и при Δu=0 при произвольном α, так как оно превращается в тождество 0=0. При Δu=0 будем полагать α=0. Разделим все члены полученного равенства на Δx
![]() .
.
По
условию ![]() .
Поэтому, переходя к пределу при Δx→0,
получим y 'x= y 'u·u
'x .
Теорема доказана.
.
Поэтому, переходя к пределу при Δx→0,
получим y 'x= y 'u·u
'x .
Теорема доказана.
Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от "внешней" функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от "внутренней" функции по независимой переменной.
Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y 'x осуществляется последовательным применением предыдущей теоремы.
По
доказанному правилу имеем y 'x= y 'u·u 'x .
Применяя эту же теорему для u 'x получаем ![]() ,
т.е.
,
т.е.
y 'x = y 'x· u 'v· v 'x = f 'u (u)·u 'v (v)·v 'x (x).
Примеры.
y = sin x2. Тогда
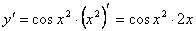 .
.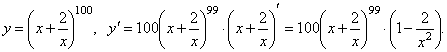
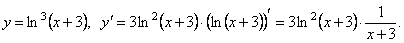
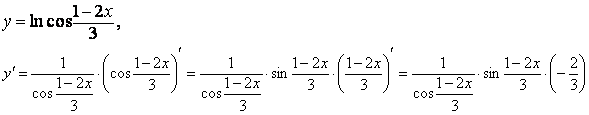
ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. Пусть u=u(x),v=v(x) – две дифференцируемые функции от переменной x.

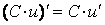 .
.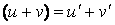 (справедлива
для любого конечного числа слагаемых).
(справедлива
для любого конечного числа слагаемых).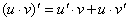 .
.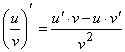 .
.
а) 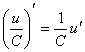 .
.
б)  .
.
Формулы 1 и 2 докажите самостоятельно.
Доказательство формулы 3.
Пусть y = u(x) + v(x). Для значения аргумента x+Δx имеем y(x+Δx)=u(x+Δx) + v(x+Δx).
Тогда
Δy=y(x+Δx) – y(x) = u(x+Δx) + v(x+Δx) – u(x) – v(x) = Δu +Δv.
Следовательно,
![]() .
.
Доказательство формулы 4.
Пусть y=u(x)·v(x). Тогда y(x+Δx)=u(x+Δx)·v(x+Δx), поэтому
Δy=u(x+Δx)·v(x+Δx) – u(x)·v(x).
Заметим, что поскольку каждая из функций u и v дифференцируема в точке x, то они непрерывны в этой точке, а значитu(x+Δx)→u(x), v(x+Δx)→v(x), при Δx→0.
Поэтому можем записать
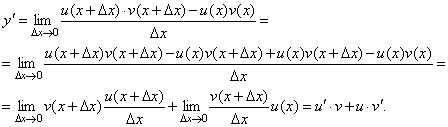
На основании этого свойства можно получить правило дифференцирования произведения любого числа функций.
Пусть, например, y=u·v·w. Тогда,
y ' = u '·(v·w) + u·(v ·w) ' = u '·v·w + u·(v '·w +v·w ') = u '·v·w + u·v '·w + u·v·w '.
Доказательство формулы 5.
Пусть ![]() . Тогда
. Тогда

При доказательстве воспользовались тем, что v(x+Δx)→v(x) при Δx→0.
Примеры.
Если
 ,
то
,
то 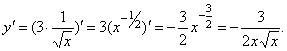
y = x3 – 3x2 + 5x + 2. Найдем y '(–1).
y ' = 3x2 – 6x+ 5. Следовательно, y '(–1) = 14.
y = ln x · cos x, то y ' = (ln x) ' cos x + ln x (cos x) ' =1/x∙cos x – ln x · sin x.

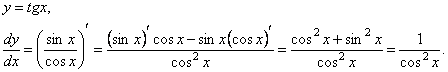
Таким образом,
![]()
Аналогично для y= ctgx,
![]()
y = xn. Если n – целое положительное число, то, используя формулу бинома Ньютона:
(a + b)n = an+n·an-1·b + 1/2∙n(n – 1)an-2∙b2+ 1/(2∙3)∙n(n – 1)(n – 2)an-3b3+…+ bn,
можно доказать, что
![]()
Итак, если x получает приращение Δx, то f(x+Δx) = (x + Δx)n, и, следовательно,
Δy=(x+Δx)n – xn =n·xn-1·Δx + 1/2·n·(n–1)·xn-2·Δx2 +…+Δxn.
Заметим, что в каждом из пропущенных слагаемых есть множитель Δx в степени выше 3.
Найдем предел
![]()
Мы доказали эту формулу для n N. Далее увидим, что она справедлива и при любом n R.
y= sin x. Вновь воспользуемся определением производной.
Так как, f(x+Δx)=sin(x+Δx), то
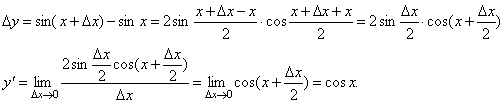
Таким образом,
![]()
Аналогично можно показать, что
![]()
Рассмотрим функцию y= ln x.
Имеем f(x+Δx)=ln(x+Δx). Поэтому
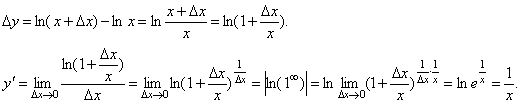
Итак,
![]()
Используя свойства логарифма можно показать, что
![]()
Формулы 3 и 5 докажите самостоятельно.
11
ПОНЯТИЕ ОБРАТНОЙ ФУНКЦИИ
Начнем
с примера. Рассмотрим функцию y=
x3.
Будем рассматривать равенство y= x3 как
уравнение относительно x.
Это уравнение для каждого
значения у определяет
единственное значение x: Прежде чем перейти к общему случаю, введем определения. Функция y = f(x) называется возрастающей на некотором отрезке, если большему значению аргумента x из этого отрезка соответствует большее значение функции, т.е. если x2>x1, то f(x2) > f(x1). Аналогично функция называется убывающей, если меньшему значению аргумента соответствует большее значение функции, т.е. еслих2 < х1 , то f(x2) > f(х1). Итак, пусть дана возрастающая или убывающая функция y= f(x), определенная на некотором отрезке [a; b]. Для определенности будем рассматривать возрастающую функцию (для убывающей все аналогично). Рассмотрим два различных значения х1 и х2. Пусть y1=f(x1), y2=f(x2). Из определения возрастающей функции следует, что если x1<x2, то у1<у2. Следовательно, двум различным значениям х1 и х2 соответствуют два различных значения функции у1 и у2. Справедливо и обратное, т.е. если у1<у2, то из определения возрастающей функции следует, чтоx1<x2. Т.е. вновь двум различным значениям у1 и у2 соответствуют два различных значенияx1 и x2. Т.о., между значениями x и соответствующими им значениями y устанавливается взаимно однозначное соответствие, т.е. уравнение y=f(x)для каждого y (взятого из области значений функции y=f(x)) определяет единственное значение x, и можно сказать, что x есть некоторая функция аргумента y: x= g(у). |
|
Эта функция называется обратной для функции y=f(x). Очевидно, что и функция y=f(x) является обратной для функции x=g(у).
Заметим, что обратная функция x=g(y) находится путем решения уравнения y=f(x) относительно х.
Пример. Пусть дана функция y = ex. Эта функция возрастает при –∞ < x <+∞. Она имеет обратную функцию x = lny. Область определения обратной функции 0 < y < + ∞.
Сделаем несколько замечаний.
Замечание 1. Если возрастающая (или убывающая) функция y=f(x) непрерывна на отрезке [a; b], причем f(a)=c, f(b)=d, то обратная функция определена и непрерывна на отрезке [c; d].
Замечание 2. Если функция y=f(x) не является ни возрастающей, ни убывающей на некотором интервале, то она может иметь несколько обратных функций.
П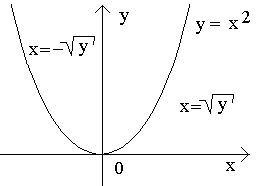 ример. Функция y=x2 определена
при –∞<x<+∞.
Она не является ни возрастающей, ни
убывающей и не имеет обратной функции.
Однако, если мы рассмотриминтервал
0≤x<+∞,
то здесь функция является возрастающей
и обратной для нее будет
ример. Функция y=x2 определена
при –∞<x<+∞.
Она не является ни возрастающей, ни
убывающей и не имеет обратной функции.
Однако, если мы рассмотриминтервал
0≤x<+∞,
то здесь функция является возрастающей
и обратной для нее будет ![]() .
На интервале – ∞ <x≤
0 функция – убывает и обратная для нее
.
На интервале – ∞ <x≤
0 функция – убывает и обратная для нее ![]() .
.
Замечание 3. Если функции y=f(x) и x=g(y) являются взаимно обратными, то они выражают одну и ту же связь между переменными x и y. Поэтому графикомих является одна и та же кривая. Но если аргумент обратной функции мы обозначим снова через x, а функцию через y и построим их в одной системе координат, то получим уже два различных графика. Легко заметить, что графики будут симметричны относительно биссектрисы 1-го координатного угла.
ТЕОРЕМА О ПРОИЗВОДНОЙ ОБРАТНОЙ ФУНКЦИИ
Докажем теорему, позволяющую находить производную функции y=f(x), зная производную обратной функции.
Теорема. Если
для функции y=f(x) существует
обратная функция x=g(y),
которая в некоторой точке у0 имеет
производную g'(v0),
отличную от нуля, то в соответствующей
точке x0=g(x0)
функция y=f(x) имеет
производную f '(x0),
равную ![]() ,
т.е. справедлива формула
,
т.е. справедлива формула![]() .
.
Доказательство. Т.к. x=g(y) дифференцируема в точке y0, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x)непрерывна в точке x0=g(y0). Следовательно, при Δx→0 Δy→0.
Покажем,
что ![]() .
.
Пусть ![]() .
Тогда по свойству предела
.
Тогда по свойству предела ![]() .
Перейдем в этом равенстве к пределу при
Δy→0.
Тогда Δx→0
и α(Δx)→0,
т.е.
.
Перейдем в этом равенстве к пределу при
Δy→0.
Тогда Δx→0
и α(Δx)→0,
т.е. ![]() .
.
Следовательно,
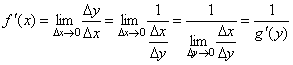 ,
,
что и требовалось доказать.
Эту
формулу можно записать в виде ![]() .
.
Рассмотрим применение этой теоремы на примерах.
Примеры.
y = ex. Обратной для этой функции является функция x= ln y. Мы уже доказали, что
 .
Поэтому согласно сформулированной
выше теореме
.
Поэтому согласно сформулированной
выше теореме
![]()
Итак,
(ex) ' = ex |
Аналогично можно показать, что (ax) ' = ax·lna. Докажите самостоятельно.
y = arcsin x. Рассмотрим обратную функцию x = sin y. Эта функция в интервале – π/2<y<π/2 монотонна. Ее производная x ' = cos y не обращается в этом интервале в нуль. Следовательно, по теореме о производной обратной функции
![]() .
.
Но
на (–π/2; π/2) ![]() .
.
Поэтому
![]()
Аналогично
![]()
Докажите самостоятельно.
y = arctg x. Эта функция по определению удовлетворяет условию существования обратной функции на интервале –π/2< y < π/2. При этом обратная функция x = tg y монотонна. По ранее доказанному
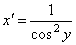 .
.
Следовательно, y '
= cos2 y .
Но ![]() .
.
Поэтому
![]()
![]()
Используя эти формулы, найти производные следующих функций:
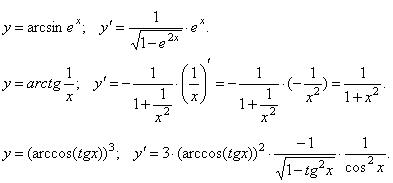
12
ТЕОРЕМА О ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ
Пусть y = f(u), а u= u(x). Получаем функцию y, зависящую от аргумента x: y = f(u(x)). Последняя функция называется функцией от функции или сложной функцией.
Областью определения функции y = f(u(x)) является либо вся область определения функции u=u(x) либо та ее часть, в которой определяются значения u, не выходящие из области определения функции y= f(u).
Операция "функция от функции" может проводиться не один раз, а любое число раз.
Установим правило дифференцирования сложной функции.
Теорема. Если функция u= u(x) имеет в некоторой точке x0 производную и принимает в этой точке значение u0 =u(x0), а функция y= f(u) имеет в точке u0 производную y 'u= f '(u0), то сложная функция y = f(u(x)) в указанной точке x0 тоже имеет производную, которая равна y 'x= f '(u0)·u '(x0), где вместо u должно быть подставлено выражение u= u(x).
Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументуu на производную промежуточного аргумента по x.
Доказательство. При фиксированном значении х0 будем иметь u0=u(x0), у0=f(u0). Для нового значения аргумента x0+Δx:
Δu= u(x0 + Δx) – u(x0), Δy=f(u0+Δu) – f(u0).
Т.к. u – дифференцируема в точке x0, то u – непрерывна в этой точке. Поэтому при Δx→0 Δu→0. Аналогично при Δu→0 Δy→0.
По условию . Из этого соотношения, пользуясь определением предела, получаем (при Δu→0)
,
где α→0 при Δu→0, а, следовательно, и при Δx→0.
Перепишем это равенство в виде:
Δy= y 'uΔu+α·Δu.
Полученное равенство справедливо и при Δu=0 при произвольном α, так как оно превращается в тождество 0=0. При Δu=0 будем полагать α=0. Разделим все члены полученного равенства на Δx
.
По условию . Поэтому, переходя к пределу при Δx→0, получим y 'x= y 'u·u 'x . Теорема доказана.
Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от "внешней" функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от "внутренней" функции по независимой переменной.
Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y 'x осуществляется последовательным применением предыдущей теоремы.
По доказанному правилу имеем y 'x= y 'u·u 'x . Применяя эту же теорему для u 'x получаем , т.е.
y 'x = y 'x· u 'v· v 'x = f 'u (u)·u 'v (v)·v 'x (x).
Примеры.
y = sin x2. Тогда .