1

Функция — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Элементарные функции — функции, которые можно получить с помощью конечного числаарифметических действий и композиций из следующих основных элементарных функций:

• многочлен,

• рациональная,

• степенная,

• показательная и логарифмическая,

• тригонометрические и обратные тригонометрические.

Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывнына своей области определения. Иногда к основным элементарным функциям относят такжегиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.

Рациональная функция — это дробь, числителем и знаменателем которой являютсямногочлены

Степенна́я фу́нкция — функция y = x^a, где a (показатель степени) — некоторое вещественное число.^[1] К степенным часто относят и функцию вида y = kx^a, где k — некоторый масштабный множитель

Показательная функция — математическая функция  , где a называется «основанием», а x — «показателем» степени.

Логарифмическая функция

Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию y = log _ax (см. рис. 1). Она определена при  . Область значений:  .

Функция является строго возрастающей при a > 1 и строго убывающей при 0 < a < 1. График любой логарифмической функции проходит через точку (1;0). Функция непрерывна и неограниченно дифференцируема всюду в своей области определения.

Тригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот от центрального угла в круге). 

Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

Сложная функция – функция от функции. Если z – функция от у, т.е. z(y), а у, в свою очередь, – функция от х, т.е. у(х), то функция f(x) = z(y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.

В такой функции х – независимая, а у – промежуточная переменная. При этом сложная функция определена для тех значений независимой переменной, для которых значения промежуточной функции у входят в область определения функции z(y).

Ограниченная функция. Пусть функция (одного или многих переменных) определена на множестве D. Если множество ее значений ограничено, когда аргумент (аргументы) пробегают все множество D, функция называется ограниченной. Соответственно, если множество значений функции ограничено сверху (снизу), то функция также называется ограниченной сверху (снизу).

• Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).

• Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричная относительно оси ординат).

Определение

Функция   является обратной к функции  , если выполнены следующие тождества:

• f(g(y)) = y для всех 

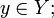
• g(f(x)) = x для всех 

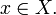
[Править]Существование

Чтобы найти обратную функцию, нужно решить уравнение x = F(y) относительно y. Если оно имеет более чем один корень, то функции обратной к F не существует. 

Примеры:

2

Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Предел функции является обобщением понятияпредела последовательности: изначально, под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.

Функция   имеет предел   в точке  , предельной для области определения функции  , если для каждой окрестности предела   существует проколотая окрестность точки  , образ которой при отображении   является подмножеством заданной окрестности точки  .