3 Теоремы о пределах

1. Бесконечно большие и бесконечно малые.

Функция f(x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение  > 0, что для всех x удовлетворяющих неравенству xa < имеет место неравенство f(x) > M.

lim_x a=

2. Функция ограниченная при x a.

3. Функция ограниченная при x .

4. Теорема. Если lim_x a f(x)=b, то функция f(x) ограниченная при x a.

5. Бесконечно малые и их свойства. lim_x a (x)=0

Теорема. 1. Если f(x)=b+, где  - б.м. при x a, то lim_x a f(x)=b и обратно, если lim_x af(x)=b, то можно записать f(x)=b+(x).

Теорема. 2. Если lim_x a (x)=0 и (x)  0, то 1/ .

Теорема. 3. Сумма конечного числа б.м. есть б.м.

Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.

6. Теоремы о пределах.

Теорема. 1. Предел суммы есть сумма пределов.

Теорема. 2. Предел произведения есть произведение пределов.

Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).

Теорема. 4. Если u(x)  z(x)  v(x), и lim_x a u(x)=lim_x a v(x)=b, то lim_x a z(x)=b. ("Теорема о двух милиционерах").

Доказательства

ТЕОРЕМЫ О ПРЕДЕЛАХ

Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.

.

Доказательство. Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится так же. Пусть .Тогда f(x)=b+α(x) и g(x)=c+β(x), где α и β – бесконечно малые функции. Следовательно,

f(x) + g(x)=(b + c) + (α(x) + β(x)).

Так как b + cесть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то

.

Пример.  .

Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:

.

Доказательство. Пусть  . Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Произведение bc есть величина постоянная. Функция bβ + c α + αβ на основании свойств бесконечно малых функций есть величина бесконечно малая. Поэтому  .

Следствие 1. Постоянный множитель можно выносить за знак предела:

.

Следствие 2. Предел степени равен степени предела:

.

Пример. .

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.

.

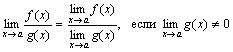Доказательство. Пусть  . Следовательно, f(x)=b+α(x) и g(x)=c+β(x), где α, β – бесконечно малые. Рассмотрим частное

.

Дробь  является бесконечно малой функцией, так как числитель есть бесконечно малая функция, а знаменатель имеет предел c²≠0.

Примеры.

1. .

2. .

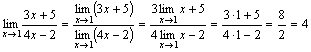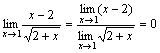3. Рассмотрим 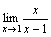 . При x→1 числитель дроби стремится к 1, а знаменатель стремится к 0. Но так как  , т.е. 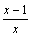 есть бесконечно малая функция при x→1, то  .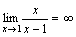

Т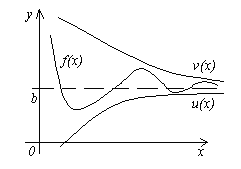 еорема 4. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е. если

, то  .

Смысл этой теоремы понятен из рисунка.

Доказательство теоремы 4 можно найти, например, в учебнике: Пискунов Н. С. Дифференциальное и интегральное исчисления, т. 1 – М.: Наука, 1985.

Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределуb, то этот предел не может быть отрицательным: b≥0.

Доказательство. Доказательство проведем методом от противного. Предположим, что b<0, тогда |y – b|≥|b| и, следовательно, модуль разности не стремится к нулю при x→a. Но тогда y не стремится к пределу b при x→a, что противоречит условию теоремы.

Теорема 6. Если две функции f(x) и g(x) при всех значениях аргумента x удовлетворяют неравенству f(x)≥ g(x) и имеют пределы  , то имеет место неравенство b≥c.

Доказательство. По условию теоремы f(x)-g(x) ≥0, следовательно, по теореме 5  , или  .

3