
- •1.1.1. Качественные измерения
- •1.1.2. Количественные измерения
- •1.1.3. Квазиколичественные измерения
- •1.2. Типы представления многомерных данных
- •1.2.1. Матрица «объект-признак»
- •Матрицы с пропусками данных
- •Основные схемы данных типа «объект-признак»
- •1.2.2. Случайная векторная переменная
- •1.2.3. Ковариационная и корреляционные матрицы
- •1.2.4. Матрицы близостей
- •1.2.5. Нечеткие методы представления данных
- •Основные характеристики нечетких множеств
- •Операции над нечеткими множествами
- •Нечеткая лингвистическая переменная
- •Упражнения и задачи
- •Литература
1.2.4. Матрицы близостей
Ряд
процедур статистической обработки,
такие как Q-факторный
и кластерный анализы, многомерное
шкалирование, анализ соответствий
использует в качестве исходных данных
квадратную матрицу
![]() «объект-объект»
размерности
п×п,
элементами
которых являются меры сходства или
различий
«объект-объект»
размерности
п×п,
элементами
которых являются меры сходства или
различий
![]() между объектами
и
,
между объектами
и
,
![]() [4,
6, 8]. Каждая строка и каждый столбец
матрицы
соответствует одному объекту. Элементом
в i-й
строке и j-м
столбце матрицы
является мера сходства между объектами
i
и j.
[4,
6, 8]. Каждая строка и каждый столбец
матрицы
соответствует одному объекту. Элементом
в i-й
строке и j-м
столбце матрицы
является мера сходства между объектами
i
и j.
Количественное
оценивание сходства тесно связано с
понятием метрика.
Пусть
объекты представлены точками координатного
пространства и меру сходства или различия
оценивают в соответствии с метрическим
расстоянием между
точками. В метрическом пространстве
каждой паре элементов Хi
и
Хj
поставлено
в соответствие расстояние, обозначаемое
![]() .
Для того, чтобы мера сходства была
метрикой любых объектов Хi
, Хj
и Хk,
она
должна удовлетворять аксиомам:
.
Для того, чтобы мера сходства была
метрикой любых объектов Хi
, Хj
и Хk,
она
должна удовлетворять аксиомам:
1)
![]() для
всех
(аксиома тождества);
для
всех
(аксиома тождества);
2)
![]() для всех
(аксиома треугольника);
для всех
(аксиома треугольника);
3)
![]() для
всех
(аксиома симметрии).
для
всех
(аксиома симметрии).
Важность метрики как меры сходства неоспорима, однако она не является единственным способом описания сходства объектов. Существует несколько видов сходства, в которых меры не являются метриками. Например, оценивание сходства объектов может основываться на процессе сопоставления признаков. Такое понятие сходства не связано с размерностью пространства. Более того, в социальных исследованиях сходство объектов оценивают непосредственно. Например, при определении сходства за основу берут степень взаимосвязи объектов. В этих случаях часто нарушается аксиома симметрии: А соответствует В, но В соответствует А не в той же степени. Нарушение симметрии вызывает определенные трудности при исследованиях, но применение таких мер может оказаться целесообразным и необходимым при решении конкретных задач. Рассмотрим некоторые меры сходства.
Корреляционная матрица «объект-объект». Пусть признаки в матрице «объект-признак» измерены в количественной шкале. За меру сходства двух объектов в этой матрице возьмем квадратный корень из коэффициента корреляции
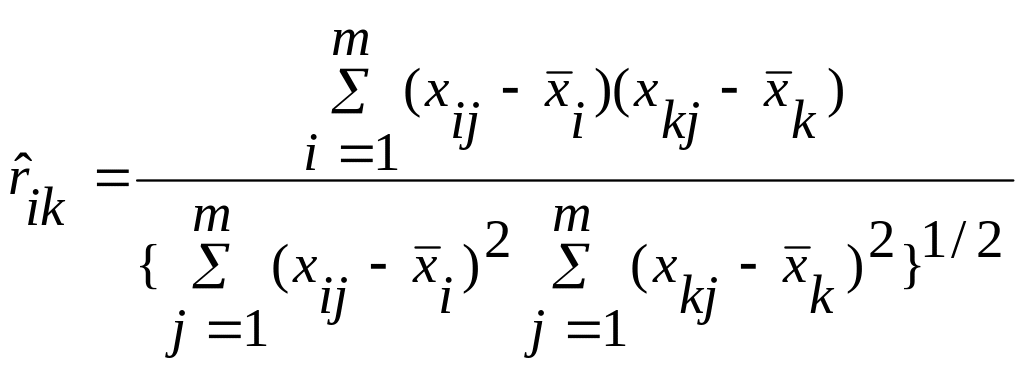 ,
,
![]() (1.12)
(1.12)
где
-
значение
j-й
переменной для i-го
объекта;
![]() -
среднее для всех переменных i-го
объекта; п
- число объектов; т
-
число признаков. Вычисленные
коэффициенты корреляции образуют
корреляционную матрицу типа «объект-объект»
размерности п×п.
Если
признаки измерены в номи-нальной или в
порядковой шкале, то вместо
используются
соответственно коэффициенты
сопряженности и ранговой корреляции.
-
среднее для всех переменных i-го
объекта; п
- число объектов; т
-
число признаков. Вычисленные
коэффициенты корреляции образуют
корреляционную матрицу типа «объект-объект»
размерности п×п.
Если
признаки измерены в номи-нальной или в
порядковой шкале, то вместо
используются
соответственно коэффициенты
сопряженности и ранговой корреляции.
Коэффициенты
корреляционной матрицы «объект-объект»
в отличие от корреляционной матрицы
«признак-признак» не имеют ясного
физического смысла, так как средние
![]() в
формуле
(1.12) определяются по всем признакам
одного объекта. Поэтому полученный
коэффициент отражает форму, но не
чувствителен к различиям в величине
переменных, используемых при вычислении
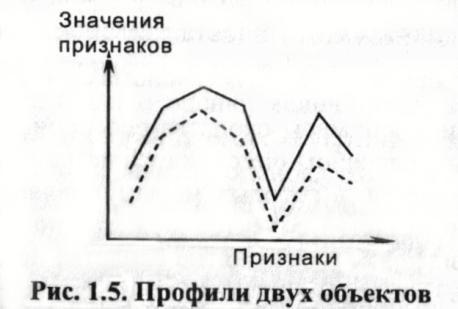
коэффициента. Чувствительность к форме
особенно важна в таких науках, как
социология, психология и антропология,
в которых используются профили. Профиль
- это вектор значений признаков объекта,
изображенный в виде ломаной линии. Два
профиля могут иметь корреляцию, равную
1, но не будут идентичными (рис. 1.5).
в
формуле
(1.12) определяются по всем признакам
одного объекта. Поэтому полученный
коэффициент отражает форму, но не
чувствителен к различиям в величине
переменных, используемых при вычислении
коэффициента. Чувствительность к форме
особенно важна в таких науках, как
социология, психология и антропология,
в которых используются профили. Профиль
- это вектор значений признаков объекта,
изображенный в виде ломаной линии. Два
профиля могут иметь корреляцию, равную
1, но не будут идентичными (рис. 1.5).
Недостатком корреляционной матрицы «объект-объект» как меры сходства является то, что элементы этой матрицы не удовлетворяют аксиоме треугольника. Эта мера является полезной в приложениях кластерного анализа и многомерного шкалирования, где важна форма, а не сдвиг и масштаб. Если нужно анализировать не меру сходства, а меру различий, то корреляции нужно преобразовать в различия:
![]() .
.
Меры расстояния. Для этой меры большому расстоянию соответст- вует меньшее сходство. Поэтому эту меру лучше бы называть мерой несходства, различия. Меры расстояния не ограничены сверху и зависят от выбора масштаба измерений. Если исходные данные заданы матрицей «объект-признак» X, то возможно вычисление различных типов расстояний между объектами Хi и Хj.
Одним из наиболее часто применяемых расстояний является расстояние Минковского.
![]() ,
,
где![]() - весовые коэффициенты при признаках;
- весовые коэффициенты при признаках;
![]() - параметр степени. Веса выражают степень
важности измерения при различении
объектов. При сопоставлении двух объектов
измерениям признака с меньшей значимостью
нужно присваивать меньшие веса. Назначение
весов признаков можно осуществить
посредством линейного преобразования.
В
тех случаях,
когда линейное преобразование сводится
к изменению масштабов,
матрица весов является диагональной
- параметр степени. Веса выражают степень
важности измерения при различении
объектов. При сопоставлении двух объектов
измерениям признака с меньшей значимостью
нужно присваивать меньшие веса. Назначение
весов признаков можно осуществить
посредством линейного преобразования.
В
тех случаях,
когда линейное преобразование сводится
к изменению масштабов,
матрица весов является диагональной
![]() .
Параметр степени, как установили
психологи, представляет собой монотонную
функцию
от степени внимательности.
.
Параметр степени, как установили
психологи, представляет собой монотонную
функцию
от степени внимательности.
Это расстояние нужно применять тогда, когда все признаки матрицы X взаимонезависимы и однородны, например, измерены в одних и тех же единицах и одинаково важны для решаемой задачи. Частными случаями расстояния Минковского являются:
а) евклидово расстояние
![]() ,
,
![]() ,
,
![]() ,
,
б) манхеттингское расстояние (расстояние «Сити-блок»)
![]() ,
,
![]() ,
,
![]() ,
,
в) доминантное расстояние
![]() ,
,
,
,![]() .
.
Расстояние Махаланобиса
![]() ,
,
где
![]() ,
,
![]() -
векторы переменных объектов i
и j,
-
векторы переменных объектов i
и j,
![]() -
обратная корреляционная матрица
признаков. Это расстояние применяется
при сильной зависимости
и
физической неоднородности исследуемых
признаков. В отли-чие от евклидовой
метрики и метрики Минковского, эта
метрика через ковариационную матрицу
связана с корреляциями признаков. Если
признаки некоррелированы, то расстояние
Махаланобиса эквивалентно евклидовому
расстояние.
-
обратная корреляционная матрица
признаков. Это расстояние применяется
при сильной зависимости
и
физической неоднородности исследуемых
признаков. В отли-чие от евклидовой
метрики и метрики Минковского, эта
метрика через ковариационную матрицу
связана с корреляциями признаков. Если
признаки некоррелированы, то расстояние
Махаланобиса эквивалентно евклидовому
расстояние.
Несмотря на важность рассмотренных метрик, они имеют серьезные
недостатки. Наиболее существенным недостатком является то, что оценка сходства сильно зависит от различий в сдвигах признаков. Если одно-временно велики абсолютные значения и стандартные отклонения при-знаков, то эти признаки могут подавить влияние переменных с меньшими абсолютными значениями и стандартными отклонениями. Для уменьшения указанных влияний можно использовать нормированные признаки с нулевыми средними и единичными дисперсиями. Однако нормировка также может сильно повлиять на меру сходства.
Хеммингово
расстояние. В
теории кодирования количество разрядов,
в которых кодовая комбинация А
отличается
от кодовой комбинации B,
называется хемминговым
расстоянием
![]() между
этими комбинациями. Нетрудно убедиться,
что хеммингово расстояние удовлетворяет
всем трем аксиомам метрики, а именно:
1)
между
этими комбинациями. Нетрудно убедиться,
что хеммингово расстояние удовлетворяет
всем трем аксиомам метрики, а именно:
1)
![]() тогда и только тогда, когда комбинации
А и В тождественно равны, 2)
тогда и только тогда, когда комбинации
А и В тождественно равны, 2)
![]() и
3) для любых трех комбинаций выполняется
аксиома треугольника
и
3) для любых трех комбинаций выполняется
аксиома треугольника
![]() .
.
Пример 1.6. Кодовые комбинации 00 и 11 отстоят друг от друга дальше, чем 00 от 01 или 01 от 11.
В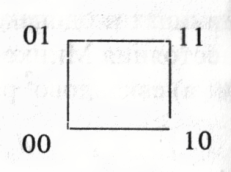 этом случае четыре комбинации можно
изобразить графически, поместив их в
вершинах квадрата. В общем случае кодовые
комбинации будут помещаться в вершинах
единичного гипер-куба, размерность
которого равна числу классов.
этом случае четыре комбинации можно
изобразить графически, поместив их в
вершинах квадрата. В общем случае кодовые
комбинации будут помещаться в вершинах
единичного гипер-куба, размерность
которого равна числу классов.
В
данном примере максимальное хеммингово
расстояние равно 2 Можно определить
также относительное расстояние, поделив
это расстояние на 21/2,
а в случае длины кода
![]() на
на
![]() .
.
Из изложенного ясно, что хеммингово расстояние можно использовать как меру расстояния между объектами, заданными категоризованными, в частности дихотомическими, признаками
![]() ,
,
где
![]() ,
если у
,
если у
![]() и
и
![]() совпали
категории k-го
признака;
совпали
категории k-го
признака;
![]() ,
если категории k-го
признака различны.
,
если категории k-го
признака различны.
Прямые оценки различия. Для оценки различий пар объектов необ-ходимо осуществить выборку из генеральной совокупности объектов и предъявить их экспертам. Выборка объектов должна быть случайной и для обеспечения обоснованной оценки различий эксперты должны быть знакомы с объектами. После построения выборок объектов и экспертов исследователь должен решить, какой тип задания для оценки различий нужно дать испытуемым. На практике получили распространение четыре типа заданий: оценка величины различия, категориальная оценка, графическая оценка и категориальная сортировка.
В задании по оценке величины различия одна пара объектов берется в качестве стандарта. Эксперт должен приписать каждой оцениваемой паре число, показывающее степень различия этой пары относительно различия стандартной пары. В качестве оценки различия любой пары объектов можно взять среднегеометрическое или, реже, медиану приписанных экспертами чисел.
Дня получения прямых оценок различий наиболее часто используют категориальные оценки, содержащие от шести до девяти уровней. Эксперту предъявляют пару объектов (А и В) и просят приписать число из заданной шкалы уровней следующим образом:
Максимально Максимально
похожи различны
A: В ------ ----- ----- ----- ----- ----- ----- ----
(0) (1) (2) (3) (4) (5) (6) (7)
В качестве оценки различия пары объектов берется среднеарифметическая величина оценок, приписанных ей всеми экспертами.
Метод категориальных сортировок является по существу вариантом категориальных оценок. Испытуемому предъявляют в случайном порядке карточки с парами объектов и требуют от него разложить эти карточки в некотором порядке. При этом он должен отнести пару очень похожих пар объектов в самую низшую категорию. Для каждой пары оценку различия получаем как среднеарифметическое приписанных ей оценок.
Заметим, что при большом числе объектов трудно произвести прямые сравнения. Для п объектов число сравнений равно (n2 - n)/2 пар. Например, при п = 50 получаем 1225 сравнений. Один из способов уменьшения числа сравнений состоит в следующем. Каждый объект Аi, принимают за стандартный и остальные (n - 1) объектов упорядочивают по отношению к стандартному объекту. При этом ранговое место 1 занимает объект, который был более всех схож со стандартным. Диагональные элементы матрицы близостей заполняют нулями. Полученная таким образом матрица не является симметричной.
Условные
и совместные вероятности. В
качестве мер близости объектов можно
использовать матрицы условной и
совместной вероятности, элементами
которых являются вероятности
![]() .
Методы
построения этих матриц подробно изложены
в работе [6].
.
Методы
построения этих матриц подробно изложены
в работе [6].
При
применении условной вероятности в
качестве меры сходства объектов (или
событий)
![]() и
и
![]() служит вероятность появления объекта
при наличии объекта
.
Если применяются совместные вероятности,
то в качестве меры сходства объектов
(событий)
и
берется вероятность того, что объекты
и
встречаются
вместе. Эти вероятности рассматриваются
как меры сходства, а не различия.
служит вероятность появления объекта
при наличии объекта
.
Если применяются совместные вероятности,
то в качестве меры сходства объектов
(событий)
и
берется вероятность того, что объекты
и
встречаются
вместе. Эти вероятности рассматриваются
как меры сходства, а не различия.
Получаемые матрицы, как правило, являются несимметричными и элементы симметричной матрицы близостей определяют по формуле:
![]() .
.
