Вопросы для самоконтроля

1. Выведите уравнение плоскости _, проходящую через точку с нормальным вектором .

2. Укажите способы взаимного расположение двух плоскостей в пространстве.

3. Выведите формулу расстояния от точки до плоскости : .

4. Запишите нормальное уравнение плоскости . Укажите связь общего уравнения плоскости с нормальным уравнением.

5. Запишите условие перпендикулярности и параллельности плоскостей в пространстве

6. Выведите уравнение плоскости _, проходящей через три различные точки: , , .

7. Как расположена данная плоскость 5х–2y+3=0.

8. Составить уравнение плоскости, проходящей через точку А(1; 0; 2) с нормальным вектором .

9. Составить уравнение плоскости, проходящей через три различные точки

М₁ (3; 0; 1), М₂ (–1; 1; 0) и М₃ (2; 3; –2).

10. Составить уравнение плоскости, проходящей через точки М₁ (1; 2; 0) и

М₂ (2; 1; 1) и параллельный плоскости вектор .

11. Составить уравнение плоскости, проходящей через точку М₁ (3; 0; 1) и два вектора, параллельных плоскости и .

12. Найти угол между двумя плоскостями:

и .

13. Как плоскость расположена относительно оси ?

14. Составить уравнение плоскости, которая содержит оси и и проходит через начало координат.

15. Как расположена плоскость относительно плоскости ?

16. Как расположена данная плоскость .

17. Запишите формулу для нахождения расстояния от точки 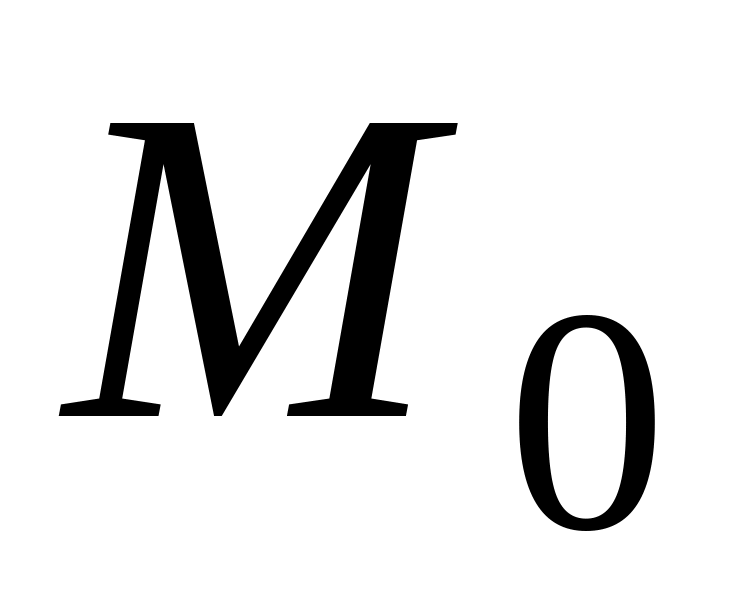до плоскости.

18. Запишите формулы для нахождения угла между плоскостями.

19. Запишите уравнение плоскости проходящей через точку и параллельно двум векторам , заданных своими координатами.

20. Как расположена данная плоскость .

Практическое занятие № 2 Плоскость. Способы задания плоскостей. Взаимное расположение плоскостей

Задача 1 Составить уравнение плоскости, заданное нормальным вектором и проходящей через точку .

Решение. Уравнение плоскости проходящей через точку с нормальным вектором , который перпендикулярен плоскости находится по формуле

,

.

Ответ.

Задача 2 Составить уравнение плоскости , проходящей через точку перпендикулярно прямой, проходящей через точки и .

Р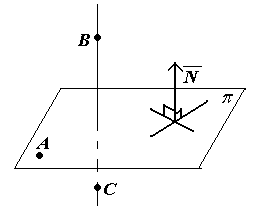 ешение.

Так как вектор перпендикулярен плоскости, то он может являться нормальным вектором для плоскости. Уравнение плоскости проходящей через точку с нормальным вектором , который перпендикулярен плоскости находится по формуле

Рисунок 39

Найдем координаты вектора . и . Подставим в данную формулу

.

.

Ответ. .

Задача 3 Составить уравнение плоскости , проходящей через точки , , .

Решение.

У равнение плоскости , проходящей через 3точки , ,

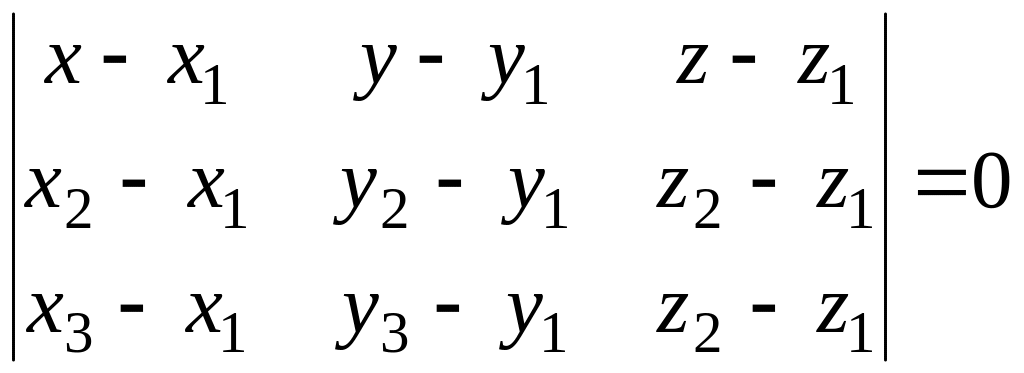
Рисунок 40

Рассмотрим точку лежащую на плоскости.

Вектора , , - компланарны их смешанное произведение равно 0, т.е. ( , , )=0. Так как точки , , , получим

, .

Ответ.

Задача 4 Составить уравнение плоскости , проходящей через точки и параллельно вектору .

Решение.

Р ассмотрим любую точку лежащую в плоскости и рассмотрим три вектора , и . Эти три вектора , , лежат в плоскости , а значит они компланарны. Смешанное произведение трех

векторов равно 0, т.е. ( , , )=0.

Рисунок 41

Найдем координаты векторов , .

Ответ.

З адача 5 Составить уравнение плоскости , проходящей через точку , параллельно вектору и параллельно вектору .

Решение.

Рассмотрим любую точку , лежащую в плоскости . При помощи параллельного переноса Рисунок 42 вектора и перенесем в плоскость . Рассмотрим три

вектора , , . Эти вектора лежат в плоскости , т.е. они компланарны. По признаку компланарности трех векторов их смешанное произведение равно 0, т.е. ( , , )=0. Так как , , , найдем координаты вектора . Подставим координаты векторов в формулу .

Ответ.

З адача 6 Составить уравнение плоскости проходящей через точку параллельно плоскости .

Решение.

Так как плоскости параллельны, то их нормальные вектора коллинеарны , значит для плоскости нормальный вектор может быть вектор . Воспользуемся формулой

- уравнение плоскости, Рисунок 43

проходящей через точку

с нормальным вектором . Подставив данные значения, получим

, .

Ответ.

Задача 7 Составить уравнение плоскости проходящей через точки и , перпендикулярно плоскости .

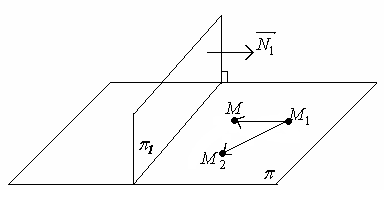
Рисунок 44

Решение.

Так как плоскости перпендикулярны то, нормальный вектор является направляющим вектором для плоскости . Рассмотрим точку лежащую в плоскости . Три вектора , и - компланарны. Смешанное произведение трех векторов равно 0, т.е.

( , , )=0. Воспользуемся формулой

Подставив данные значения в формулу, получим

.

Ответ.

Задача 8 Докажите параллельность плоскостей и , если плоскости заданы уравнениями : , : .

Решение. Так как две плоскости параллельны, то их нормальные вектора коллинеарны .

, .

Вектора коллинеарны, следовательно, плоскости параллельны.

Задача 9 Докажите перпендикулярность плоскостей и , если плоскости заданы уравнениями : , : .

Решение. Так как две плоскости перпендикулярны, то их нормальные вектора перпендикулярны, т.е. их скалярное произведение равно 0.

.

,

.

плоскости и перпендикулярны.

Задача 10 Найдите значения и при которых плоскость параллельна плоскости , если плоскости заданы уравнениями : и : .

Решение.

Плоскость с нормальным вектором .

Плоскость с нормальным вектором .

Так как две плоскости параллельны, то их нормальные вектора коллинеарны

Ответ.

Задача 11 При каком значении плоскости и перпендикулярны, если плоскости заданы уравнениями : и : .

Решение.

Плоскость с нормальным вектором . Плоскость с нормальным вектором .

Так как две плоскости перпендикулярны, то их нормальные вектора перпендикулярны и скалярное произведение этих векторов равно 0.

.

Ответ.

Задача 12 Определить двугранный угол, образованный пересечением плоскостей и , если плоскости заданы уравнениями : и : .

Решение.

Углом между плоскостями в пространстве называется угол между нормальными векторами этих плоскостей. Две плоскости и заданы уравнениями и , где , . Плоскость с нормальным вектором . Плоскость с нормальным вектором . Наименьший, из двух смежных углов, образованных этими плоскостями, находится по формуле:

Ответ.

Задача 13 Записано ли следующее уравнение плоскости в нормальном виде : ?

Решение.

Нормальное уравнение плоскости _.

Общее уравнение плоскости приводится к нормальному виду путем умножения на нормирующий множитель

,

знак перед дробью берется противоположным знаку свободного члена _.

Найдем координаты нормального вектора .

. Так как , то .

Данное уравнение записано в нормальном виде

Ответ.

Задача 14 Привести уравнение плоскости к нормальному виду .

Решение.

Нормальное уравнение плоскости _.

Общее уравнение плоскости приводится к нормальному виду путем умножения на нормирующий множитель

; знак перед дробью берется противоположным знаку свободного члена _. , .

Так как , то _. Так как нормирующий множитель _,

, .

Ответ.

Задача 15 Найти и , если плоскость задана уравнением .

Решение. Уравнение плоскости в нормальном виде: . Приведем данное уравнение к нормальному виду. . Так как , то нормирующий множитель . Умножим общее уравнение плоскости на нормирующий множитель , .

Ответ.

Задача 16 Найти расстояние от точки до плоскости, проходящей через три данные точки , , .

Решение. Расстояние от точки до плоскости : находим по формуле: .

Сначала найдем уравнение плоскости, проходящей через три различные точки: , , .

.

Ответ.

Задача 17 Найти расстояние между параллельными плоскостями и если плоскости заданы уравнениями : и : .

Решение. Для того чтобы найти расстояние между параллельными плоскостями, необходимо рассмотреть точку в одной из плоскостей и найти расстояние от этой точки до другой плоскости.

Найдем любую точку в плоскости . Пусть и , тогда . . Расстояние от точки до плоскости : находим по формуле:

.

Ответ.