Методические указания / до виконання завдань блоку змістових модулів 3

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ АВТОМОБІЛЬНО-ДОРОЖНІЙ УНІВЕРСИТЕТ

ХНАДУ

Кафедра

інженерної та комп’ютерної графіки

МЕТОДИЧНІ ВКАЗІВКИ

до виконання завдань блоку змістових модулів 3

з курсу нарисної геометрії для студентів технічних спеціальностей

Харків 2011

Міністерство освіти і науки, молоді та спорту України

ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ АВТОМОБІЛЬНО-ДОРОЖНІЙ УНІВЕРСИТЕТ

МЕТОДИЧНІ ВКАЗІВКИ

до виконання завдань блоку змістових модулів 3 з курсу нарисної геометрії

для студентів технічних спеціальностей

Затверджено методичною радою університету,

Харків

ХНАДУ

2011

Кафедра інженерної та комп’ютерної графіки

2

ЗАГАЛЬНІ ВКАЗІВКИ

Уметодичних вказівках подані рекомендації до самостійного виконання обов’язкових домашніх завдань – однієї із складових частин курсу нарисної геометрії, а саме: завдань блоку змістових модулів 3 для студентів технічних спеціальностей.

Мета роботи – засвоєння студентами теоретичного та практичного матеріалу за темами: поверхні, побудова ліній взаємного перетину поверхонь та розгортка поверхонь.

Уданих методичних вказівках розглянуті теоретичні основи, порядок та приклади виконання обов’язкових домашніх завдань третього блоку змістових модулів.

Варіанти для виконання завдань наведено в таблицях 1, 2 (додаток 1) методичних вказівок, а приклади виконання завдань наведено на рисунках 3.21 – 3.23 (додаток 2). Виконання обов’язкових домашніх завдань вимагає від студентів навичок користування літературою, перелік якої надано в методичних вказівках.

1 НАРИСНА ГЕОМЕТРІЯ

1.1 Блок змістових модулів 4 – (Розділ 1)

Теоретичні питання, що розглядаються у третьому модулі

Змістовий модуль 8 (Тема 5) Зображення. Види, розрізи, перерізи. Змістовий модуль 9 (Тема 6)

Аксонометричні проекції. Сутність метода. Поняття та визначення. Стандартні аксонометричні проекції.

1.2 Обов’язкові домашні завдання третього модуля

Самостійна робота виконується студентом індивідуально, відповідно до варіанту завдання, оформлюється у формі альбому та орієнтована на засвоєння теоретичного та практичного матеріалу, що розглядається у третьому модулі дисципліни.

3

Змістовий модуль 10 (СРС)

Завдання 7

На форматі А3 виконати кресленик моделі з розрізами, перерізами та аксонометрією. Кресленик виконати в масштабі 1:1.

Модель виконується за варіантом, який визначає викладач. Приклад виконання наведено на рисунку 3.21.

Завдання 8

На форматі А3 виконати два комплексних двокартинних кресленика в масштабі 1:1.

Варіанти завдань для графічних побудов потрібно взяти за варіантом з таблиць 1, 2 (додаток 1).

Кресленик 1. Побудувати лінію перетину двох поверхонь, одна з яких проекціювальна.

Кресленик 2. Побудувати лінію перетину двох поверхонь, використовуючи допоміжні сферичні поверхні-посередники.

Приклад виконання наведено на рисунку 3.22.

Завдання 9

На форматі А3 виконати кресленик розгортки поверхні з лінією перетину в масштабі 1:1.

Поверхня обирається студентом самостійно із завдання 8. Приклад виконання наведено на рисунку 3.23.

1.3 Запитання для самоперевірки

1.Поняття про аксонометричне проекціювання.

2.Види аксонометричних проекцій.

3.Що називається коефіцієнтом спотворення?

4.Класифікація аксонометричних проекцій за напрямком проекціювання.

5.Під якими кутами розташовано осі в прямокутній ізометрії і чому дорівнюють коефіцієнти спотворення на аксонометричних осях?

6.Під якими кутами розташовано осі в прямокутній диметрії і чому дорівнюють показники спотворення на аксонометричних осях?

7.Які проекції звуться вторинними?

8.Як розташовуються велика і мала осі еліпсів в прямокутній аксонометрії? Які їх величини в ізометрії і диметрії?

9.Що називається розгорткою поверхні?

4

10.Алгоритм побудови лінії перетину граних поверхонь?

11.Який вигляд має лінія перетину двох граних поверхонь?

12.Які існують методи побудови проекцій лінії перетину двох не проекціювальних поверхонь?

13.В чому полягає спосіб допоміжних січних площин?

14.В яких випадках застосовують метод допоміжних січних площин?

15.В якому випадку лінія перетину двох поверхонь обертання вироджується в плоскі криві?

16.При перетині яких поверхонь застосовують метод концентричних сфер?

17.При перетині яких поверхонь застосовують метод неконцентричних сфер?

18.До чого зводиться побудова лінії перетину двох поверхонь, одна з яких проекціювальна?

19.Як перетинаються між собою поверхні обертання із спільною віссю?

20.Які ви знаєте способи допоміжних сфер?

21.Сформулюйте теорему Монжа.

22.В яких випадках застосовують спосіб допоміжних сфер?

23.Який спосіб використовують при побудові розгорток циліндра та конуса?

24.Як побудувати умовну розгортку сферичної поверхні?

2 ОЦІНКА ПРАЦЕВИТРАТ СТУДЕНТА НА ЗАСВОЄННЯ ПРОГРАМИ БЛОКУ ЗМІСТОВИХ МОДУЛІВ 3

5

3 СКЛАД ОБОВ’ЯЗКОВИХ ДОМАШНІХ ЗАВДАНЬ

Завдання 7

На кресленику геометричної моделі з натури повинні бути зображені:

−три проекції моделі;

−розрізи на головному зображенні та виді зліва;

−натуральна величина фігури перерізу проекціювальною площиною, яка задана викладачем;

−аксонометрична проекція моделі.

Виконання завдання починається з аналізу поверхонь, які складають модель. У зв’язку з тим, що поверхня, яка обмежує геометричне тіло, розглядається як множина точок, необхідно розуміти, що таке обрис поверхні і як він проекціюється на площину проекцій. Деякі поверхні (циліндр, призма) можуть займати проекціювальне положення по відношенню до площин проекцій. Крім того, необхідно вірно вибрати головне зображення моделі, а потім вже у проекційному зв’язку добудувати інші зображення на головних площинах проекцій (ГОСТ 2.305-2008, п. 2.1).

Послідовність виконання завдання:

1.Накреслити 3 проекції геометричної моделі. Приділити увагу побудові проекцій ліній перетину поверхонь.

2.Виконати необхідні розрізи згідно ГОСТ 2.305-2008, п. 3. При цьому необхідно пам’ятати о різниці між розрізом та перерізом. На розрізі зображають те, що розміщено в січній площині та за нею, а у перерізі зображають тільки те, що розміщено в січній площині. Якщо деталь не симетрична, необхідно зображати її у повному розрізі. Якщо ж деталь симетрична, допускається з’єднувати половину виду з половиною розрізу. Розріз стандарти рекомендують розташовувати праворуч або знизу відносно осі симетрії. Границею виду і розрізу є осьова лінія. Якщо на осьову лінію попадає проекція ребра, тоді поруч проводять хвилясту лінію для розмежування виду і розрізу.

3.Побудувати натуральну величину фігури перерізу проекціювальною площиною.

4.Проставити розміри згідно ГОСТ 2.307-68.

5.Виконати аксонометричну проекцію геометричної моделі. Зробити виріз чверті фігури по площинам XOZ і YOZ.

Приклад виконання завдання приведений на рис. 3.21.

6

Побудова проекцій лінії перетину

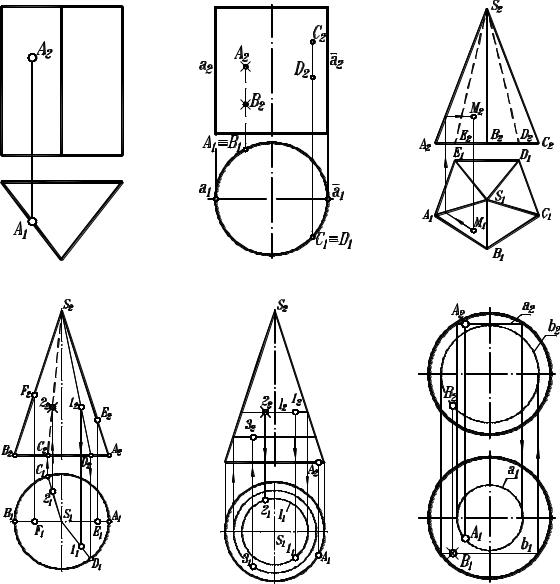
Лінія перетину двох поверхонь – це безліч точок, що належать обом поверхням. Таким чином, побудова проекцій лінії перетину зводиться до знаходження цих точок. На рисунку 3.1 (а…е) показані приклади побудови проекцій точок на різних поверхнях. Як видно з побудови, горизонтальні проекції точок, які розташовані на проекціювальних поверхнях призми (рис. 3.1, а) і циліндра (рис. 3.1, б) перебувають на лініях горизонтальних абрисів цих поверхонь. Визначення їхнього положення не вимагає додаткових побудов.

г д е Рисунок 3.1 − Побудова точок на призмі (а), циліндрі (б), піраміді (в), конусі (г, д) і сфері (е)

Точки, які розташовані на піраміді, конусі або сфері, знаходять за допомогою ознаки належності їх цим поверхням (точка належить

поверхні, якщо вона належить лінії, яка належить цій поверхні).

7

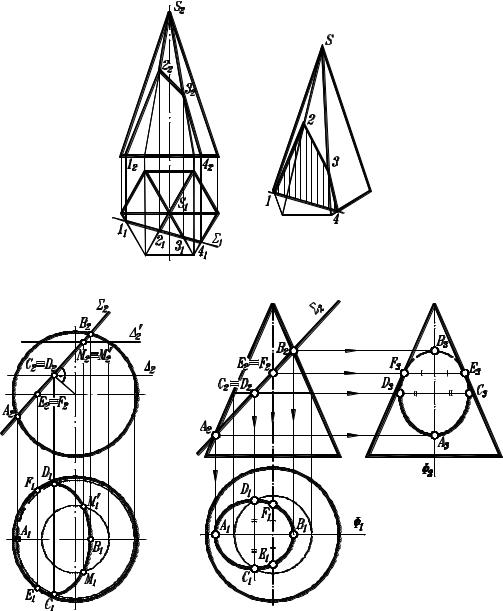
Якщо перетинаються криволінійні поверхні (циліндр, конус або сфера) із призматичною поверхнею, то лінія перетину, як правило, крива.

а

б в Рисунок 3.2 − Побудова лінії перетину поверхонь проекціювальною площиною

На рисунку 3.2 а показана побудова проекцій лінії перетину піраміди горизонтально-проекціювальною площиною. Лінія перетину багатогранних поверхонь є ламана лінія. На рисунку 3.2 б, в представлений перетин відповідно сфери й конуса фронтальнопроекціювальними площинами. Задана площина перетинає сферу по колу, що проекціюється в еліпс. В перетині конуса із заданою площиною також отримуємо еліпс.

8