тема Проекционное черчение)

Заданная плоскость Σ пересекает сферу по окружности, которая проецируется в эллипс. Мы видим, что в пересечении конуса с заданной плоскостью также получается эллипс. Исключение составляет пересечение цилиндра с многогранной поверхностью, когда какая-либо грань ее параллельна образующей цилиндра. В этом случае линия пересечения – прямая. Поняв метод посредников, можно строить проекции линии пересечения геометрических фигур

влюбом сочетании.

Впредыдущих примерах в качестве посредников применялись вспомогательные плоскости. Напомним еще об одном методе, который целесообразно применять, но только тогда, когда мы строим проекции линий пересечения поверхностей вращения. Это метод концентрических сфер (частный случай вспомогательных посред- ников-сфер). Он применим при условии, что оси поверхностей пересекаются и лежат в плоскости, параллельной какой-либо плоскости проекций.

На рис. 7, а показаны три проекции геометрической модели с фронтальным и профильным разрезами. Модель представляет собой прямой круговой цилиндр, имеющий высоту и диаметр основания по 100 мм. Вдоль вертикальной оси цилиндра имеется полость конической формы, меньшее основание которой – окружность диаметром 34 мм расположено в центре нижнего основания цилиндра, а большее – окружность диаметром 84 мм – в центре верхнего основания цилиндра. В теле цилиндра имеется цилиндрическое отверстие диаметром 56 мм, ось которого перпендикулярна фронтальной плоскости и пересекает ось цилиндра на половине его высоты.

Как видим, оси отверстий пересекаются и находятся в профильной плоскости. Следовательно, в данном случае можно использовать метод концентрических сфер. Построение трех проекций промежуточных точек A и B показано на рис. 7, а.

Проекцию одной из характерных точек, а именно точки, наиболее близко расположенной к оси конического отверстия (точки M), можно определить только этим методом (рис. 7, б). Эту точку находим при помощи наименьшей сферы, пригодной для решения данной задачи. Для определения радиуса этой сферы нужно из точки О (О3) пересечения осей провести две нормали к

10

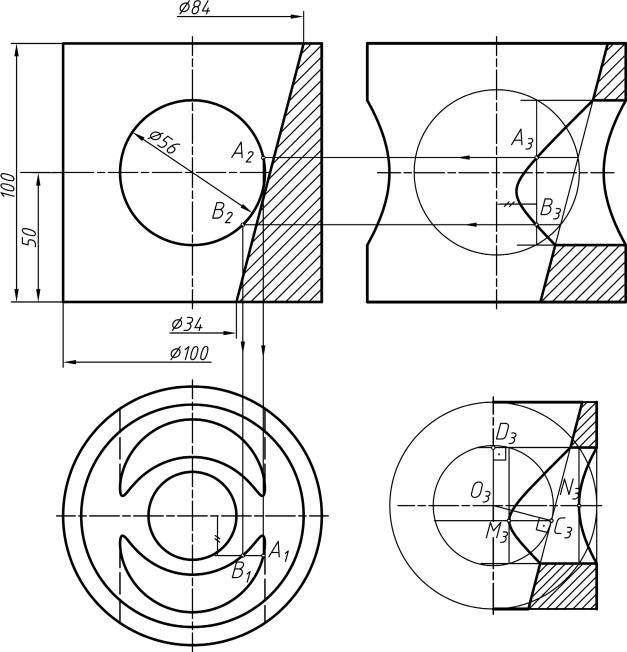
очерковым линиям конического и цилиндрического отверстий. Больший из этих отрезков (O3C3 > O3D3) определит минимальный радиус сферы. Этим же способом найдена проекция N3 аналогичной характерной точки в пересечении наружной и внутренней цилиндрических поверхностей – точки N.

Рисунок 7 – Пример использования метода сфер для построения проекций линий пересечения поверхностей вращения

11

Примеры построения натуральной величины фигуры сечения проецирующей плоскостью

На рисунке 6 (а, б, в) показано построение проекций линий пересечения геометрических фигур проецирующими плоскостями. Чтобы определить натуральную величину фигуры, ограниченной этими линиями, необходимо воспользоваться методами преобразования, известными из курса начертательной геометрии, например, методом перемены плоскостей проекций.

Рассмотрим последовательность построения натуральной величины фигуры сечения наклонной плоскостью на конкретных примерах, начиная с самых элементарных.

Пример 1. Определить натуральную величину фигуры сечения горизонтально-проецирующей призмы плоскостью А – А (рис. 8).

Рисунок 8 − Пример построения натуральной величины фигуры сечения призмы фронтально-проецирующей плоскостью

Обычно построение чертежа любого многогранника начинают с вычерчивания той проекции, где его основание проецируется в натуральную величину. В данном случае это горизонтальная проекция. Она и определяет вид и размер по ширине фронтальной проекции.

Используя наличие симметрии в фигуре, для удобства дальнейших построений выберем начало координат в центре квадратного основания. Отметим проекции точек пересечения (1, 2, 3, 4) фронтально-проецирующей плоскости А – А с ребрами призмы. Теперь построим ось сечения параллельно фронтальной проекции

12

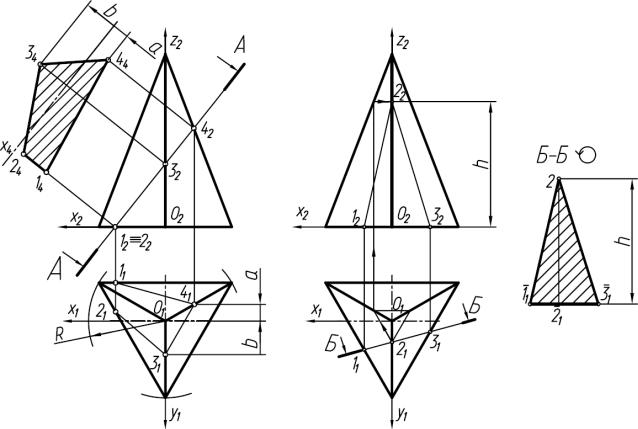
следа секущей плоскости. Ее можно расположить в любом свободном месте чертежа. Построения натуральной величины фигуры сечения, ограниченного ломаной 1-2-3-4 понятны из чертежа: от оси сечения (1 – 3)перпендикулярно ей откладывают координаты y соответствующихточек(точки2 иточки4), взятыхизгоризонтальнойпроекции.

Линии штриховки проводят под углом 45º к линии рамки чертежа или к оси сечения. В общем случае ось сечения можно также поворачивать на любой угол и располагать горизонтально или вертикально – это зависит от компоновки чертежа.

Пример 2. Определить натуральные величины фигур сечений пирамиды:

а) фронтально-проецирующей плоскостью A-A;

б) горизонтально-проецирующей плоскостью Б-Б (рис. 9).

а б Рисунок 9 – Примеры построения натуральных величин фигур сечений

пирамиды проецирующими плоскостями

Как было сказано ранее, начинаем построение с горизонтальной проекции. Поскольку основанием пирамиды является равносто-

13

ронний треугольник, начало координат целесообразно расположить в центре окружности, в которую он вписан.

Построим натуральную величину сечения пирамиды фрон- тально-проецирующей плоскостью A-A (рис. 9, а). Отметим проекции точек пересечения (1, 2, 3, 4) этой плоскости с ребрами пирамиды. Для построения натуральной величины фигуры сечения, ограниченной этой линией, преобразуем чертеж. Воспользуемся методом замены плоскостей проекций, известным из курса начертательной геометрии. Введем новую плоскость П4, заменив ею горизонтальную плоскость проекций П1, параллельно линии сечения А – А. Дальнейшие построения понятны из чертежа. Напоминаем,

что линии связи 12 – 14, 22 – 24, 32 – 34 должны быть перпендикулярны оси x4.

На рисунке 9, б показано построение натуральной величины сечения пирамиды горизонтально-проецирующей плоскостью. На виде сверху линия 11-21-31 – это и есть натуральная величина линии пересечения основания секущей плоскостью. Начертим такой же отрезок в произвольном месте и повернем его. Нахождение высоты h точки 2 показано стрелками. В данном случае необходимо указать, что сечение повернуто (символ ).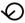

Пример 3. Определить натуральную величину фигуры сечения горизонтально-проецирующего цилиндра фронтально-проецирующей плоскостьюА– А(рис. 10).

Для удобства систему координат расположим в центре нижнего основания цилиндра. Линия пересечения цилиндра плоскостью, не параллельной его образующей или основанию, представляет собой эллипс. Определим его большую (12 - 42) и малую (31 - 3′1) оси. Для определения величины большой оси эллипса продлим линию следа секущей плоскости А-А и очерковую образующую цилиндра до их пересечения в точке 12. Малая ось равна диаметру цилиндра.

Как было сказано ранее, сечение можно располагать любым удобным образом. Построим большую ось 1-4 горизонтально. Далее строим малую ось, проходящую перпендикулярно большой оси через ее середину. По двум осям известным графическим способом строим эллипс. Ограничим точками 2 – 2′ ту его часть, которая находится в зоне поверхности цилиндра. Натуральная величина фи-

14

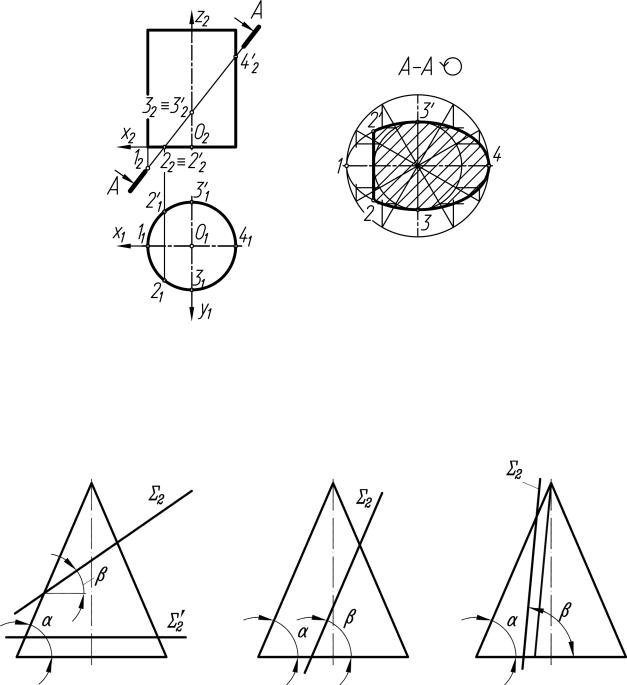
гуры сечения расположена между хордой 2 - 2′ и дугой эллипса 2-4-2′. Построения понятны из чертежа.

Рисунок 10 − Пример построения натуральной величины фигуры сечения цилиндра фронтально-проецирующей плоскостью

Пример 4. Построение конических сечений.

Нарис. 11 показаны различные положения секущей плоскостиΣ.

Рисунок 11 – Примеры конических сечений

В зависимости от углов наклона образующей конуса и секущей плоскости к основанию получаем следующие геометрические фигуры:

15

•β < α – в сечении получается эллипс (рис. 11, а);

•β = α – в сечении получается парабола (рис. 11, б);

•β > α − в сечении получается гипербола (рис. 11, в);

•Если секущая плоскость Σ' параллельна основанию конуса,

то в сечении получается фигура, подобная фигуре основания. Если конус прямой круговой, то этой фигурой является окружность (рис. 11, а).

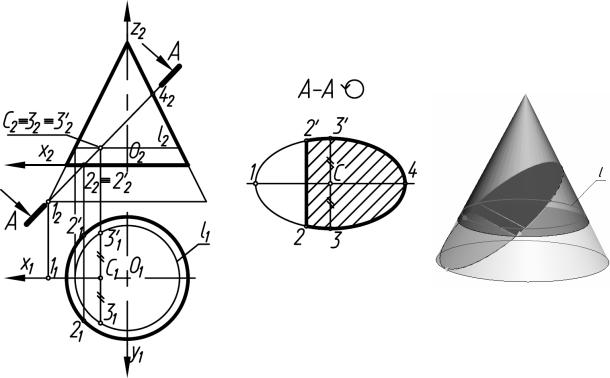
Пример 5. Построение натуральной величины фигуры сечения прямого кругового конуса фронтально-проецирующей плоскостью

(рис. 12).

Как и в предыдущих случаях, расположим систему координат удобным образом. Из рисунка мы видим, что угол наклона секущей плоскости А-А меньше угла наклона образующей конуса, и, значит, в сечении получается фигура эллипса. Продлим линии следа секущей плоскости А-А и образующей конуса до их взаимного пересечения (точка 12). Большая ось эллипса равна расстоянию 12- 42.

Рисунок 12 – Пример построения натуральной величины фигуры сечения конуса фронтально-проецирующей плоскостью

16

Чтобы найти малую ось эллипса, необходимо произвести некоторые дополнительные построения. Разделим отрезок 12-42 пополам точкой С (С2, С1). Через точку С проведем вспомогательную плоскость параллельно основанию конуса, которая пересечет конус по окружности l. В этой плоскости расположена малая ось, которая является хордой 3-3' (31-3'1) окружности l (l1). Поскольку конус ограничен основанием, то фигура сечения представляет собой часть эллипса (она заштрихована), отсеченного хордой 2-2'.

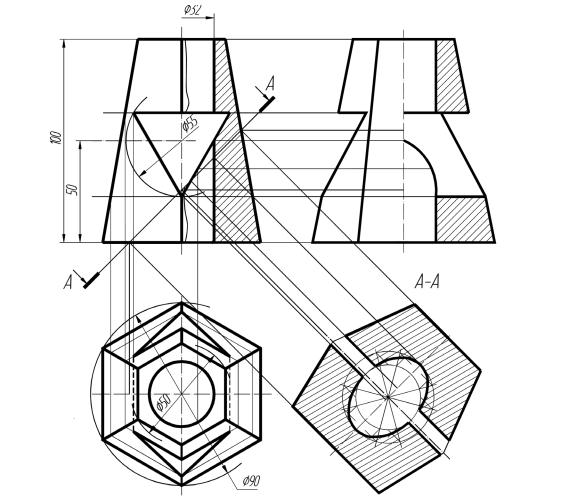
На рис. 13 показано построение натуральной величины фигуры сечения плоскостью A-A геометрической модели с двумя отверстиями. Модель представляет собой шестигранную пирамиду с вертикальным цилиндрическим отверстием и горизонтальным трехгранным призматическим отверстием.

Рисунок 13 – Пример построения натуральной величины фигуры сечения геометрической модели проецирующей плоскостью

Схематично покажем поэтапное построение (рис. 14).

17

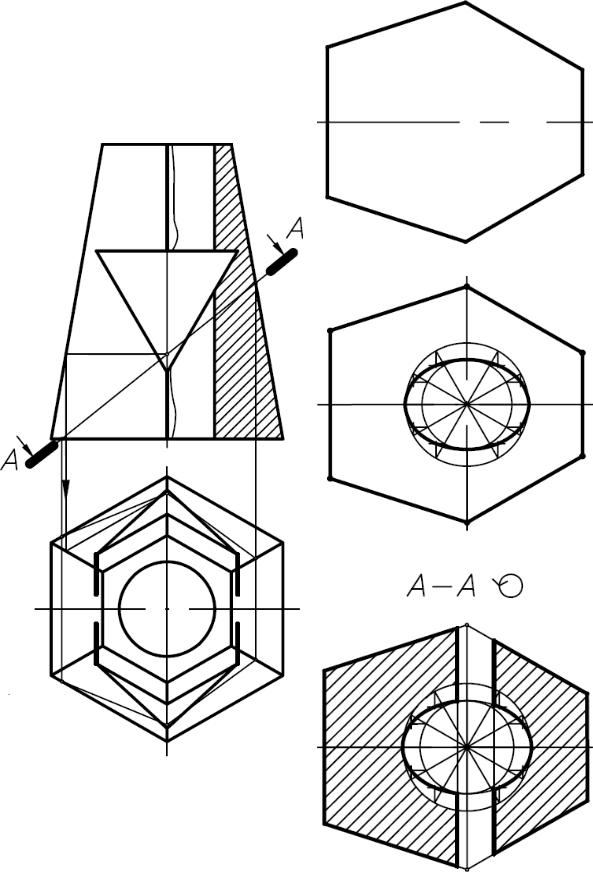
б

в

а

г

Рисунок 14 – Поэтапное построение сечения геометрической модели

18