
- •Производная
- •1.1. Определение производной
- •Правила дифференцирования
- •1.2. Дифференцирование неявных функций
- •1.3. Логарифмическое дифференцирование
- •1.4. Производные высших порядков
- •1.5. Дифференцирование функции, заданной параметрически
- •1.6. Уравнение касательной к нормали
- •2. Исследование поведения функций
- •2.1. Возрастание и убывание функции
- •2.2. Максимум и минимум функций
- •2.3. Выпуклость и вогнутость кривой. Точки перегиба
- •2.4. Асимптоты
- •3. Наибольшее и наименьшее значения функции на отрезке
- •4. Правило лопиталя
- •Задания к контрольной работе № 3
- •Библиографический список
3. Наибольшее и наименьшее значения функции на отрезке
Наибольшее и наименьшее значения функции связаны с понятием экстремума функции.
Определение.
Максимумом
![]() или минимумом
или минимумом
![]() функции
называются такие ее значения
функции
называются такие ее значения
![]() ,
для которых имеют место неравенства
,
для которых имеют место неравенства
![]() (для случая максимума) и
(для случая максимума) и
![]() (для случая минимума) при любых значениях
(для случая минимума) при любых значениях
![]() ,
положительных и отрицательных.
,
положительных и отрицательных.
Таким образом, в точках максимума (минимума) значение больше (соответственно меньше) всех соседних значений функции.
В математическом анализе понятия максимума и минимума объединяются одним словом «экстремум».
Сформулируем необходимое условие экстремума.
Если
функция
имеет в точке
![]() максимум и минимум, то ее производная
обращается в нуль в этой точке, т. е.
максимум и минимум, то ее производная
обращается в нуль в этой точке, т. е.
![]() .
.
Корни уравнения называются критическими точками функции .
Для определения экстремума в критических точках используют достаточные условия. Подробно с достаточными признаками экстремума можно ознакомиться в учебнике [1, с. 159 – 160]. Мы сформулируем правила исследования на экстремум функции.
Находим область определения функции (ООФ).
Находим критические точки. Для этого первую производную приравниваем к нулю ( ) или определяем, в каких точках производная равна или не существует.
Проверяем, принадлежат ли критические точки ООФ. Если нет, то их отбрасываем.
Проверяем знак
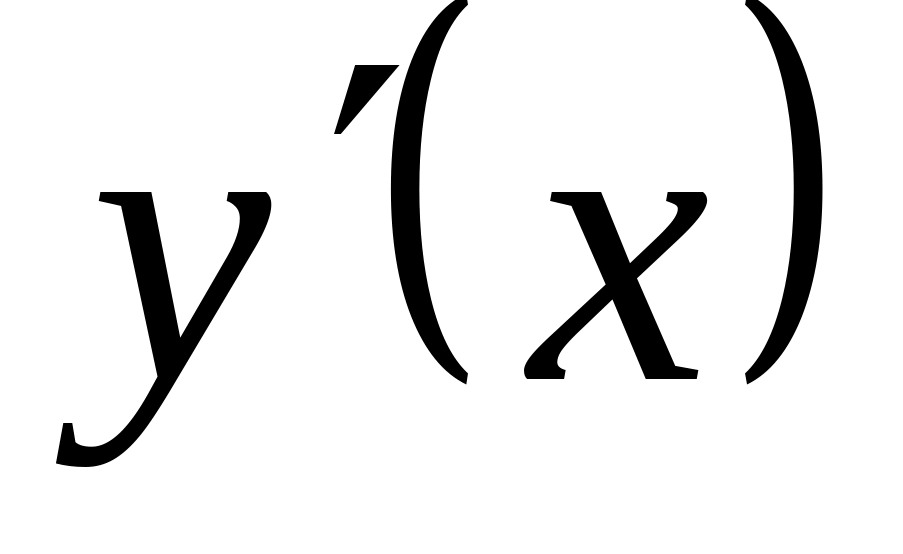 левее и правее критических точек. Если
знак меняется с плюса на минус, то в
точке максимум; с минуса на плюс, то эта
точка минимума.
левее и правее критических точек. Если
знак меняется с плюса на минус, то в
точке максимум; с минуса на плюс, то эта
точка минимума.
Пример
14. Исследовать
на экстремум функцию
![]() .
.
Решение.
1) ООФ – все действительные числа (![]() ).
).
2) Находим критические точки:
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() .
.
3)
![]() ООФ,
ООФ,
![]() ООФ,
ООФ,
![]() ООФ.
ООФ.
4)
![]() ,
если
,
если
![]() ;
; ![]() ,
если
,
если
![]() ;
;
,
если
![]() ;
,
если
;
,
если
![]() ;
;
,
если
;
,
если
![]() .
.
Значит,
в точке
данная функция достигает минимума;
![]() ;
в точке
экстремума нет; в точке
– максимум;
;
в точке
экстремума нет; в точке
– максимум;
![]() .
.
Сформулируем
правила для нахождения наибольшего и
наименьшего значения функции
на отрезке
![]() :
:
Находим ООФ.
Проверяем, принадлежат ли ООФ.
Находим критические точки.
Проверяем, принадлежат ли они .
Находим значения функции в критических точках, принадлежащих отрезку , и на концах
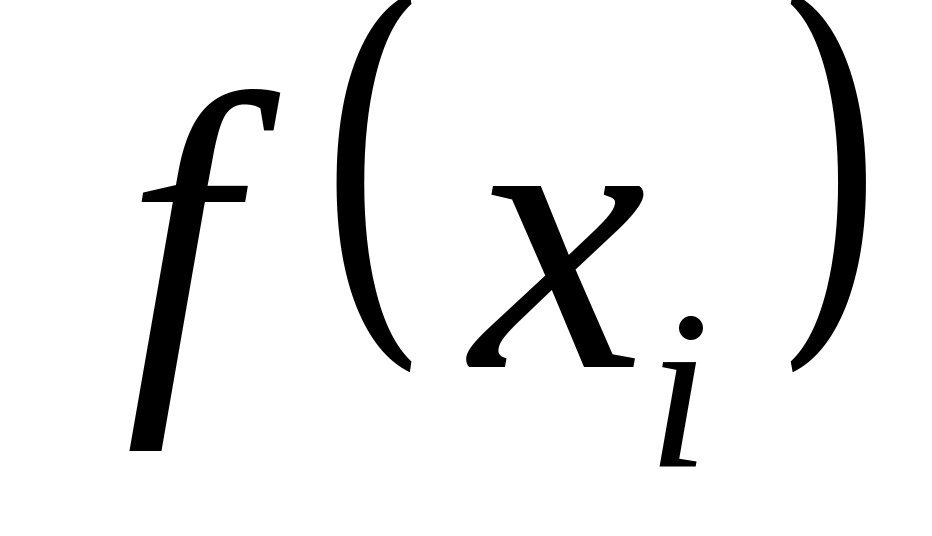 ,
,
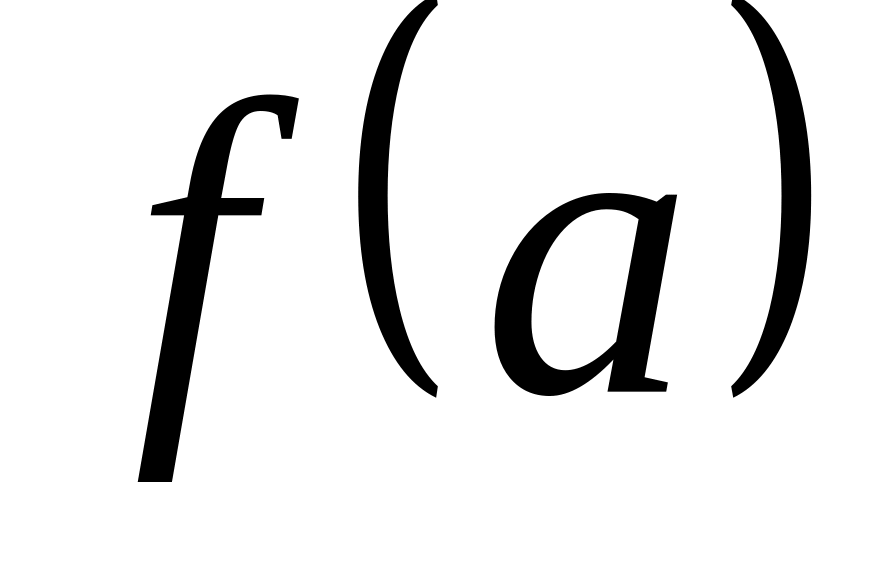 ,
,
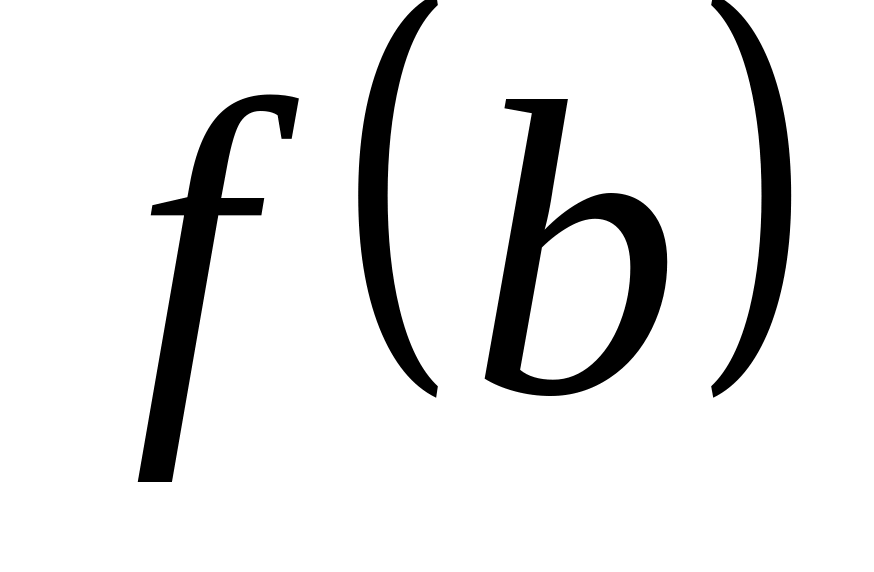 .
.Выбираем наибольшее и наименьшее значения.
Пример
15. Найти
наибольшее и наименьшее значения функции
![]() на отрезке
на отрезке
![]() .
.
Решение. 1) ООФ – все действительные числа;
2)
![]() ООФ;
ООФ;
3) Находим критические
точки:
![]() ;
;
![]() ;
;
![]() ;
; ![]() ;
; ![]()
4)
![]() ,
, ![]() ;
;
5)
![]() ;
; ![]() ;
; ![]() .
.
Ответ:
![]() ;
; ![]() .
.
Пример 16. Тело
двигалось со скоростью
![]() .
Найти наибольшую и наименьшую скорость
в течение 5 секунд движения.
.
Найти наибольшую и наименьшую скорость
в течение 5 секунд движения.
Решение. Находим
производную
![]() и критические точки
и критические точки
![]() .
Значит, внутри отрезка
.
Значит, внутри отрезка
![]() имеется только одна критическая точка
имеется только одна критическая точка
![]() .
При
функция
.
При
функция
![]() имеет максимум, равный 129, который и дает
наибольшее значение скорости:
имеет максимум, равный 129, который и дает
наибольшее значение скорости:
![]() см/с. Вычислим
при
см/с. Вычислим
при
![]() и при
и при
![]() .
Получим соответственно 1 и 116. Следовательно,
наименьшее значение скорости
.
Получим соответственно 1 и 116. Следовательно,
наименьшее значение скорости
![]() см/с; такую скорость тело имеет в начальный
момент
.
см/с; такую скорость тело имеет в начальный
момент
.
4. Правило лопиталя
При
вычислении предела отношения
![]() может оказаться, что при
может оказаться, что при
![]() числитель и знаменатель одновременно
стремятся к нулю или к бесконечности,
то есть являются одновременно бесконечно
малыми или бесконечно большими величинами.
Говорят, что в этих случаях мы имеем
дело с неопределенностями вида
числитель и знаменатель одновременно
стремятся к нулю или к бесконечности,
то есть являются одновременно бесконечно
малыми или бесконечно большими величинами.
Говорят, что в этих случаях мы имеем
дело с неопределенностями вида
![]() или
или
![]() .
Вычисление предела в этом случае
называется «раскрытием неопределенности»
и производится по правилу Лопиталя.
.
Вычисление предела в этом случае
называется «раскрытием неопределенности»
и производится по правилу Лопиталя.
Правило Лопиталя. Пусть заданы две функции и и выполняются условия:
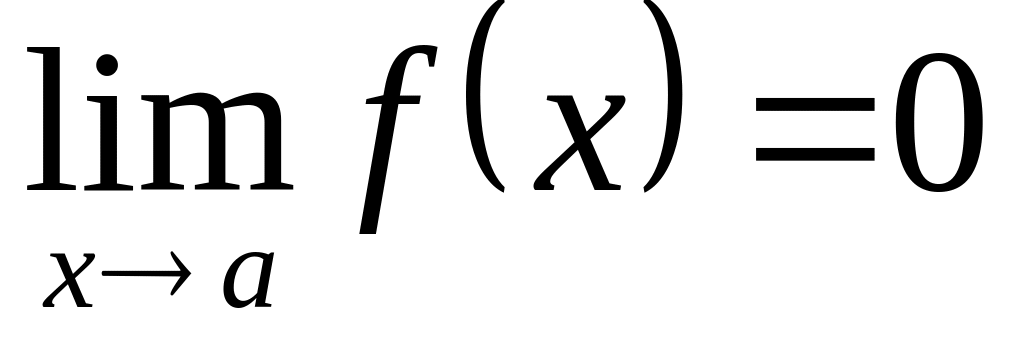 и
и
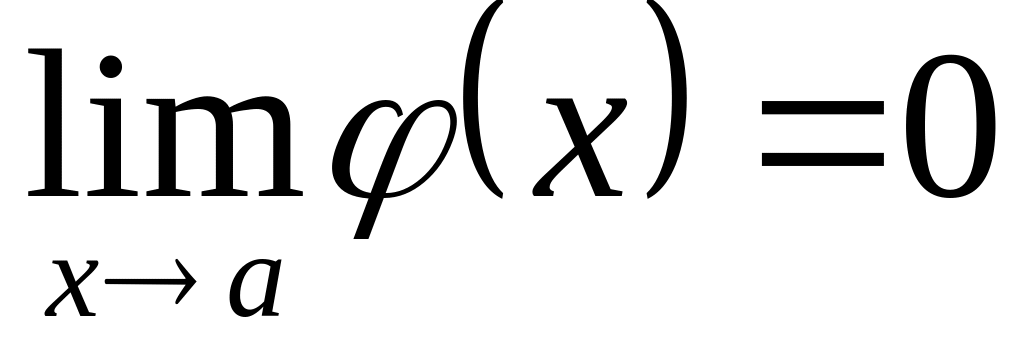 или
или
![]() и
и
![]() ;
;
они имеют первые производные в окрестности точки (за возможным исключением самой точки );
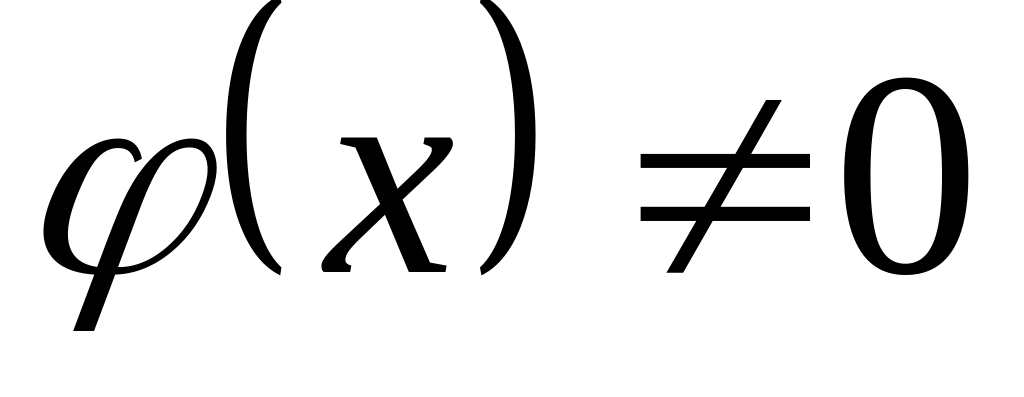 и
и
 в окрестности точки
;
в окрестности точки
;существует
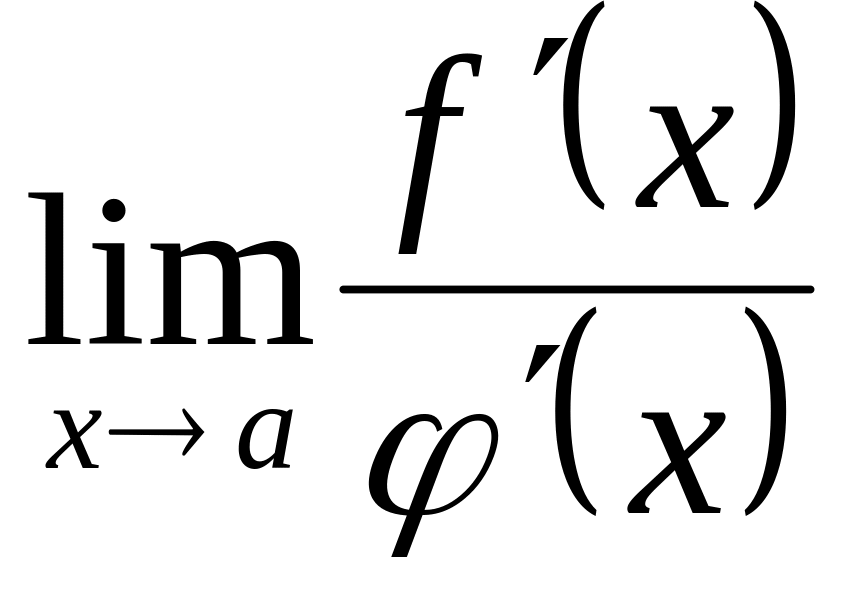 ,
тогда существует
,
тогда существует
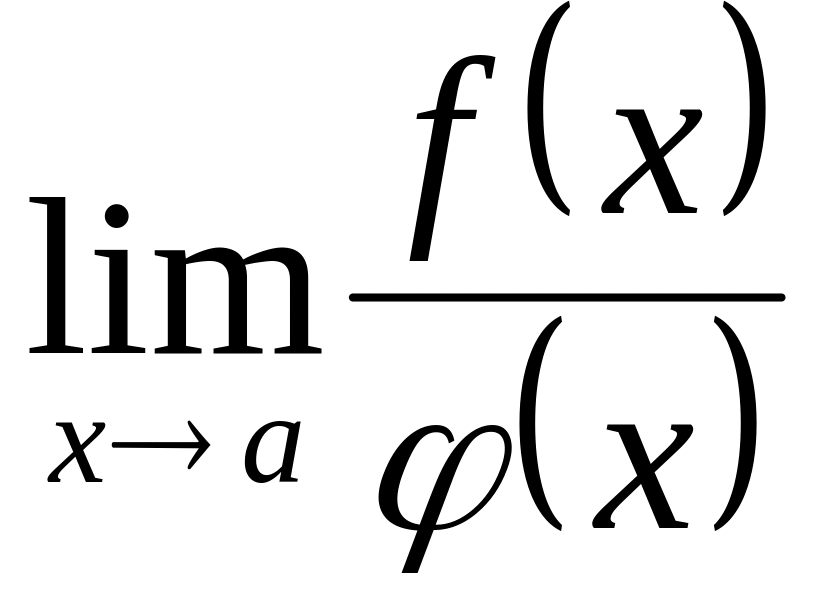 и имеет место равенство
и имеет место равенство
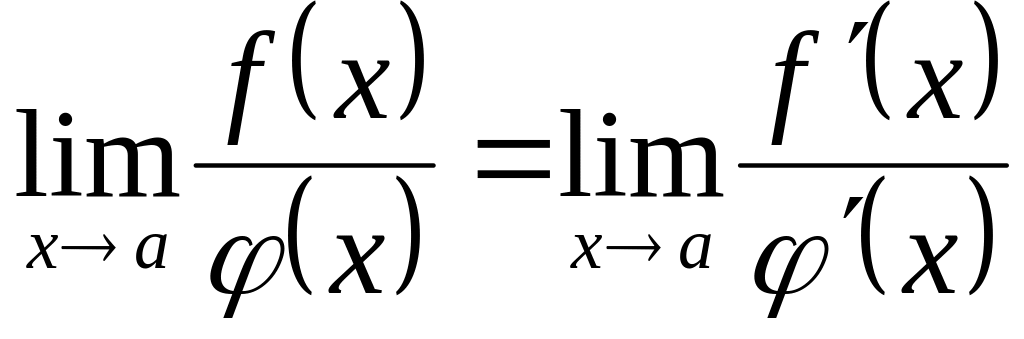 ,
если этот предел существует конечный
или бесконечный.
,
если этот предел существует конечный
или бесконечный.
Сущность этого правила состоит в том, что в случае «неопределенностей» вида или вычисление предела отношения функций, при соблюдении указанных требований, заменяется вычислением предела отношения их производных, которое в большинстве случаев оказывается проще.
В случае, когда и отношение производных приводит в «неопределенностям» вида или , снова применяют правило Лопиталя.
Пример 17.
Найти
![]() .
.
Решение.
Если в данную дробь поставить
![]() вместо
,
то получится «неопределенность» вида
.
Применяя правило Лопиталя, получим:
вместо
,
то получится «неопределенность» вида
.
Применяя правило Лопиталя, получим:
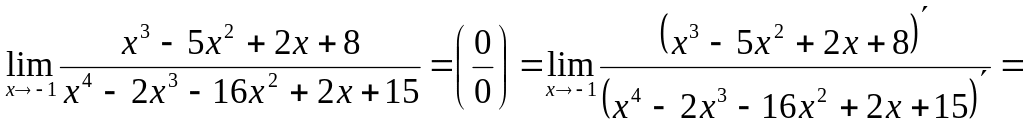
![]() .
.
Пример 18. Найти
![]() .
.
Решение. Здесь имеет место неопределенность . Применяем правило Лопиталя:
 .
.
В этом примере правило Лопиталя применили два раза.
Отметим,
что правило Лопиталя применяется для
раскрытия только «неопределенностей»
вида
и
.
Все остальные виды «неопределенностей»
(![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() )
сначала приводятся к «неопределенностям»
или
с помощью различных преобразований, а
затем применяется правило Лопиталя.
)
сначала приводятся к «неопределенностям»
или
с помощью различных преобразований, а
затем применяется правило Лопиталя.
Раскрытие «неопределенности» :
Если
![]() и
и
![]() ,
то для определения предела
,
то для определения предела
![]() надо преобразовать разность
надо преобразовать разность
![]() к виду
к виду
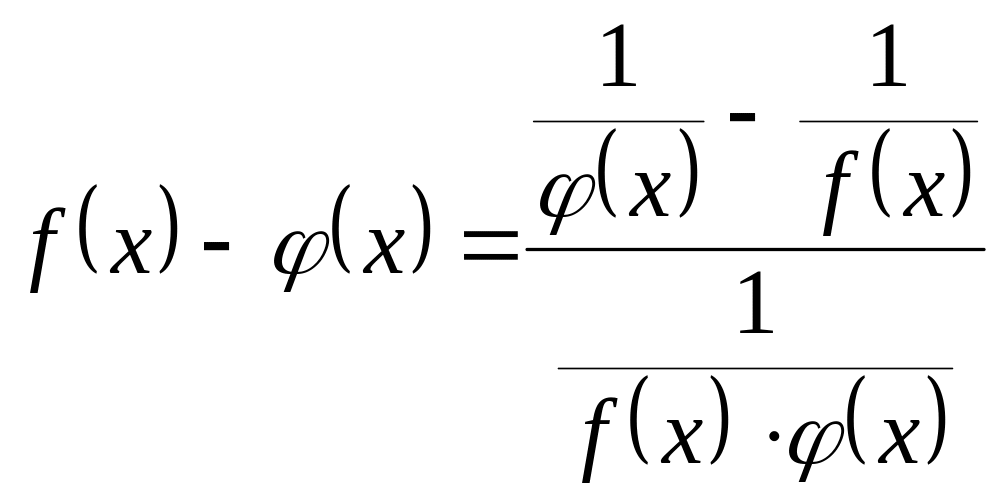 ,
,
тогда
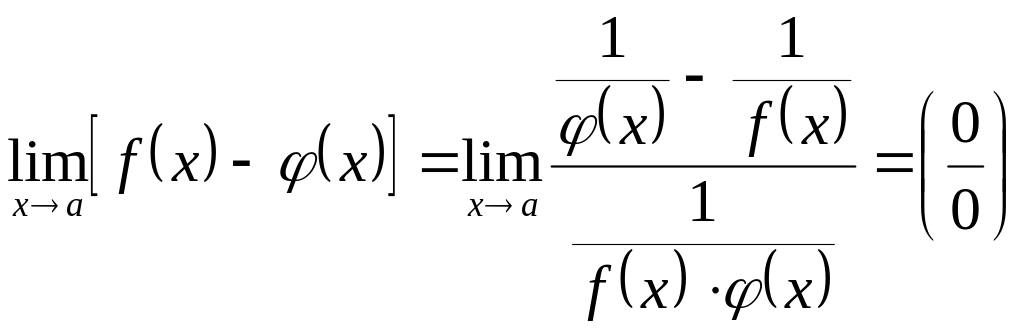
и раскрываем по правилу Лопиталя.
Пример
19. Найти
![]() .
.
Решение. Если в данную дробь поставить вместо , то получится «неопределенность» . Выражение, стоящее в скобках, приводим к общему знаменателю и получаем:
![]() .
.
Раскрытие «неопределенности» .
Пусть
,
![]() ;
;
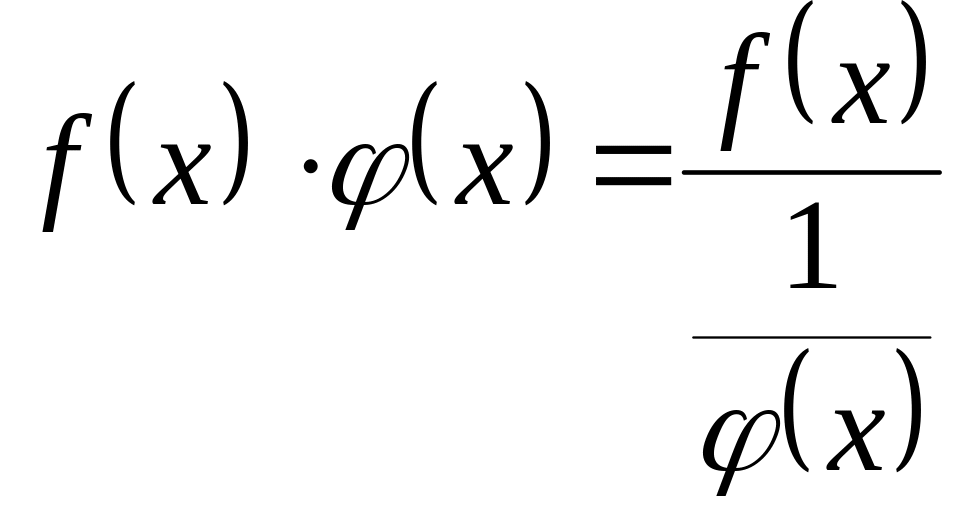 или
или
 ,
,
тогда
![]() ,
,
то есть «неопределенность» вида может быть сведена к «неопределенности» вида или .
Пример
20. Найти
![]() .
.
Решение.
При
![]()
![]() ,
а
,
а
![]() – величина бесконечно малая, поэтому
здесь имеет место «неопределенность»
вида
.
– величина бесконечно малая, поэтому
здесь имеет место «неопределенность»
вида
.
![]() .
.
«Неопределенности» вида ; ; .
«Неопределенности» этих видов сводятся к «неопределенности» вида , которая была рассмотрена выше. Это достигается с помощью тождества.
![]() ; (
; (![]() ),
),
тогда
![]() и все сводится к определению предела
и все сводится к определению предела
![]() .
.
Пример
21.
Найти
![]() .
.
Решение.
![]() ;
; ![]() ,
поэтому
,
поэтому
![]() .
.
Найдем

![]() .
.
Окончательно
получаем
![]() .
.
