1.4. Производные высших порядков

Если производная функции определена в некоторой окрестности точки и имеет в этой точке производную, то эта производная от называется второй производной (или производной второго порядка) функции в точке и обозначается одним из следующих символов:

, , , , , .

Третья производная определяется как производная от второй производной и т. д. Если уже введено понятие -й производной и если -я производная имеет производную в точке , то указанная производная называется -й производной (или производной -го порядка) и обозначается

, или , .

Таким образом, производные высших порядков определяются индуктивно по формуле:

.

Функция, имеющая -ю производную в точке , называется раз дифференцируемой в этой точке.

Пример 5. Найти функции .

Решение.

.

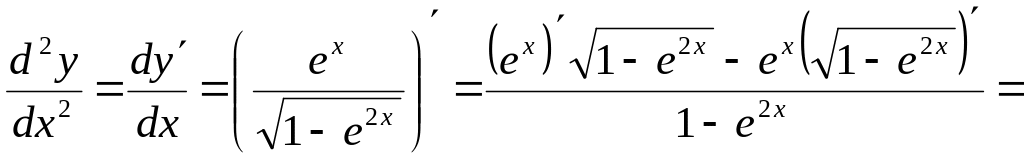
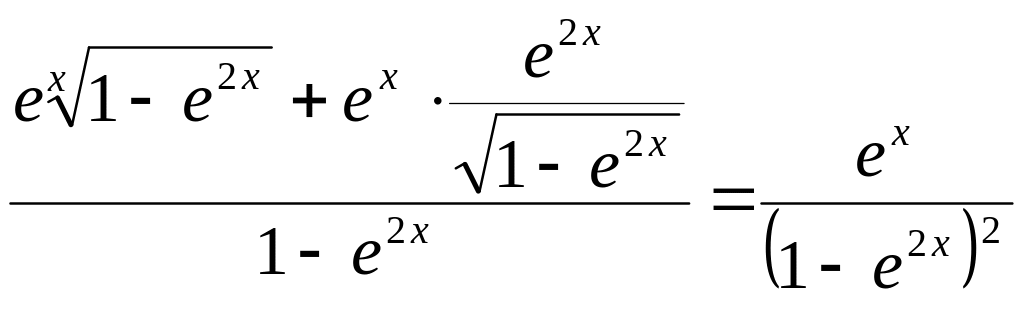Пример 6. Найти , если .

Решение. Находим .

.

Теперь найдем вторую производную . Имеем

.

1.5. Дифференцирование функции, заданной параметрически

Пусть даны две функции , (1)

где назовем параметром. Причем имеет обратную функцию . Тогда из (1) , т. е. является функцией от . Задание функции через называется параметрическим.

Если функции , имеют производные и , то функция также имеет производную, вычисляемую по формуле

. (2)

Вторая производная вычисляется по формуле

. (3)

Пример 7. Функция задана параметрически: , , . Найти и .

Решение. Найдем

.

Тогда по формуле (2) .

Для вычисления найдем .

.

Подставим в формулу (3):

.

1.6. Уравнение касательной к нормали

Касательной к линии в точке (рис. 1) называется прямая , с которой стремится совпасть секущая , когда точка , оставаясь на , стремится - будь то справа или слева.

Если линия есть график функции , то угловой коэффициент касательной равен значению производной функции в соответствующей точке.

Если график не имеет касательной, функция не имеет производной и наоборот.

Рис. 1

Эти видно из рис. 1. Угловой коэффициент секущей равен . Если стремится к , то имеет пределом угловой коэффициент касательной. Значит, , т. е. .

Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом: , значит уравнение касательной к кривой в точке , где .

Нормалью к кривой в точке называется прямая, перпендикулярная касательной. Условие перпендикулярности двух прямых: , значит уравнение нормали будет иметь вид: .

Пример 8. Составите уравнение касательной и нормали к кривой в точке . Сделать чертеж.

Решение.

, .

Уравнение касательной: .

Уравнение нормали: ; .

С делаем чертеж. – парабола, ветви направлены вниз. Вершина , , .

Т очки пересечения с осью :

,

0 1 0 1

1 -1 3,5 4