7.7. Дифференциальные уравнения Эйлера.

Дифференциальные уравнения Эйлера -уравнения движения идеальной жидкости. Уравнения Эйлера получаются из уравнений Навье -Стокса при нулевой вязкости:

Уравнения Эйлера в проекциях:

(155)

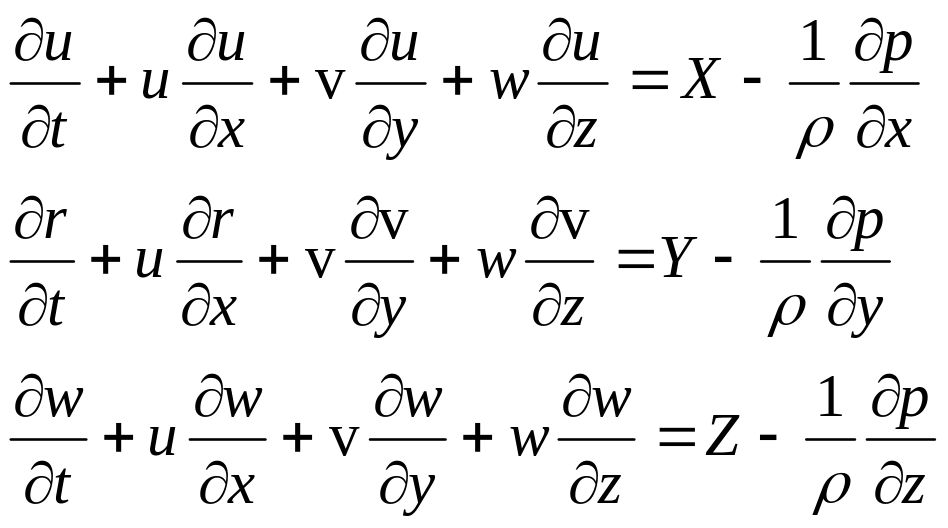
И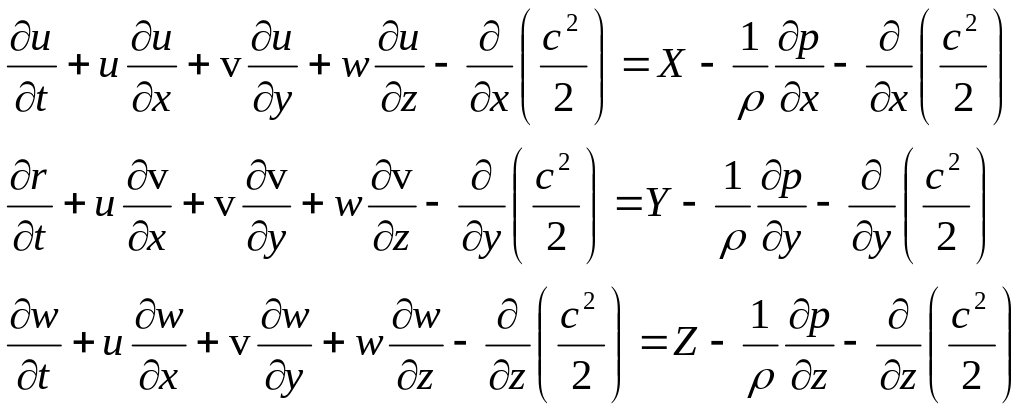 меет смысл уравнения Эйлера записать в форме, содержащей в явном виде изменение скоростей поступательного и вращательного движения. Для этого следует из обеих частей уравнений в проекциях вычесть соответствующие производные квадрата полной скорости:

Поскольку , то:

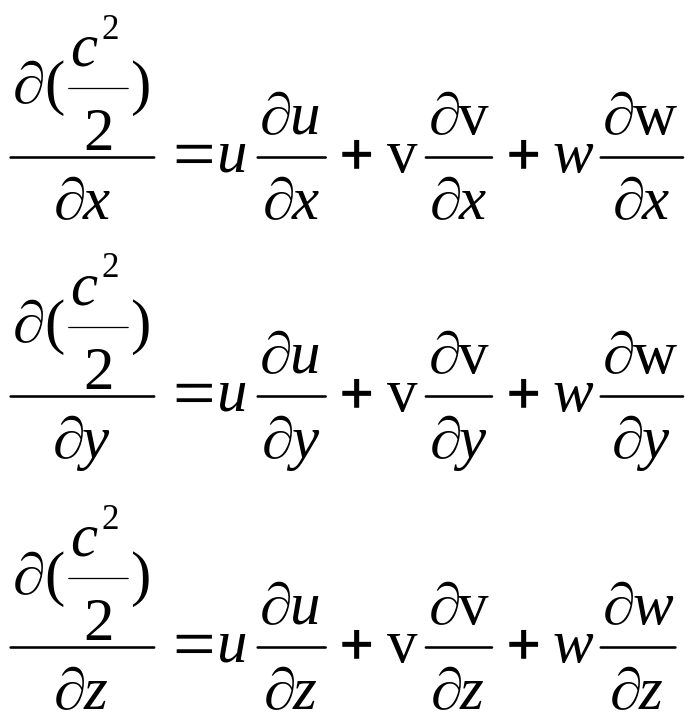
П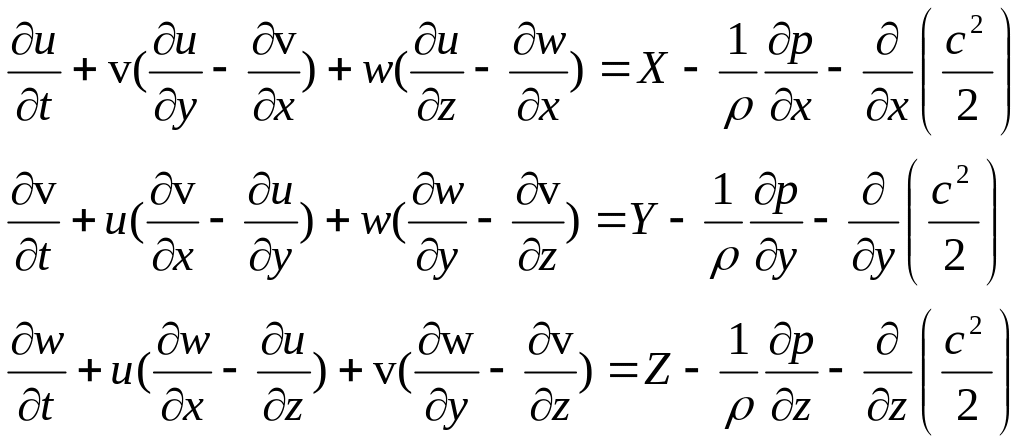 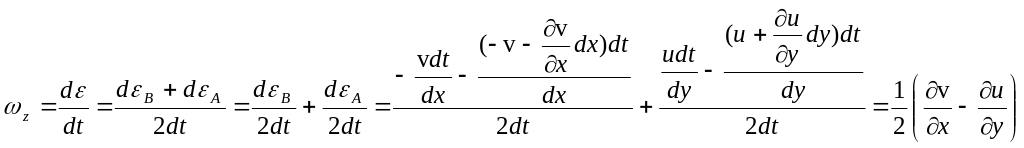ри этом члены в скобках последних уравнений представляют в явном виде компоненты вращательного движения. Действительно, деформация вращения жидкого элемента вокруг оси Z в плоскости ХОУ (рис.28) обусловлена тем, что горизонтальная составляющая скорости точки А выше горизонтальной составляющей полюса, а вертикальная составляющая точки В по модулю превышает вертикальную составляющую полюса, так что:

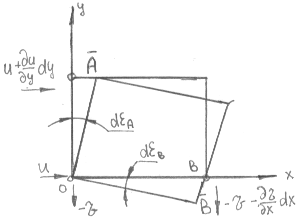
Рис.28. Деформация вращения жидкого элемента.

А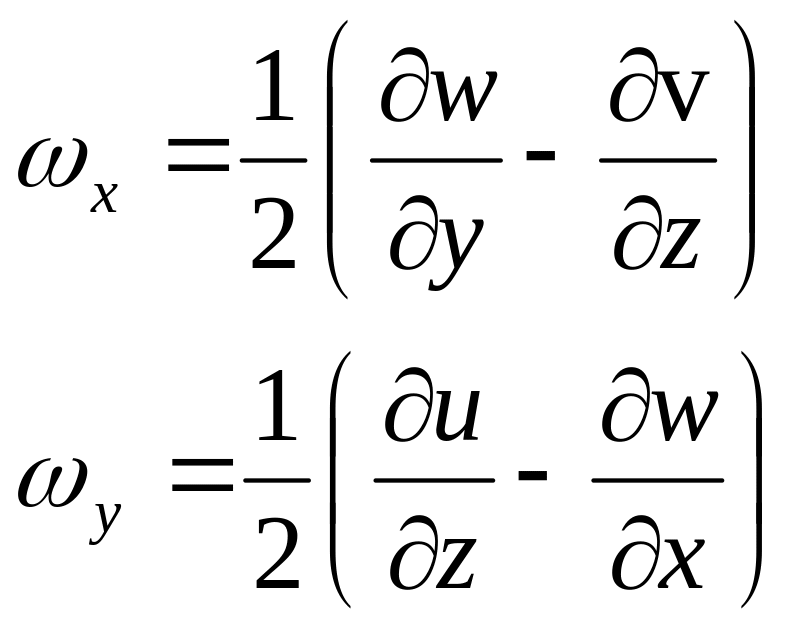 налогично:

Поэтому уравнения Эйлера можно записать так:

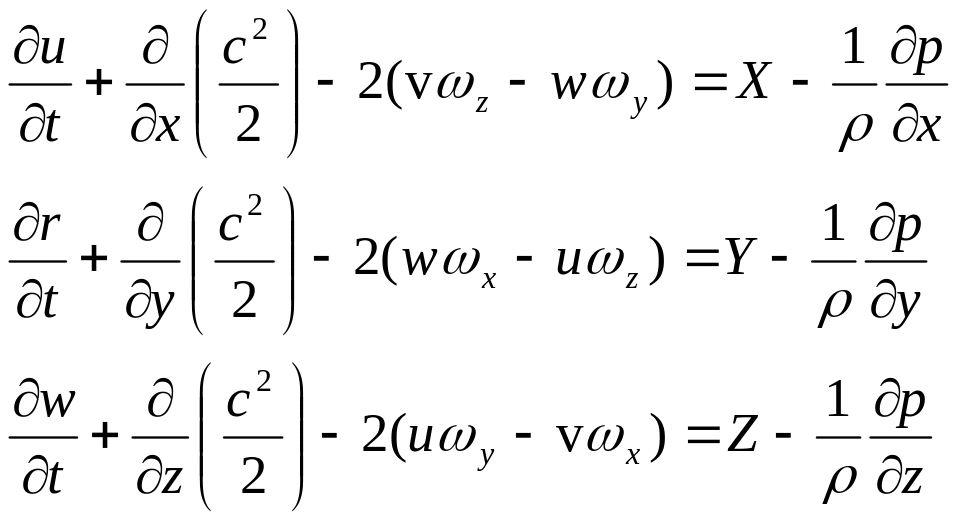
В векторной форме уравнения Эйлера, содержащие в явном виде компоненты вращательного движения (их называют уравнения Громеки -Лэмба ), имеют вид:

У равнения Эйлера могут быть проинтегрированы при некоторых условиях. Действительно, при умножении уравнений Эйлера в проекциях на элементы длины dx, dy, dz соответственно, члены уравнений приобретают некоторый новый физический смысл:

П оскольку массовые силы зависят только от координат, то полный дифференциал потенциала массовых сил М есть сумма (если существует потенциал массовых сил):

Т аким образом сумма Xdx + Ydy + Zdz представляет собой полный дифференциал массовых сил. Сумма

также является полным дифференциалом величины c²/2 ( кинетической энергии).

Е сли жидкость обладает таким свойством, что её плотность зависит только от давления (например совершенный газ в изотермическом процессе или несжимаемая жидкость с постоянной плотностью), то сумма

также является полным дифференциалом некоторой функции П [х,у,z], связанной с давлением следующим образом: dП = dP/

Е сли существует потенциал скорости как функция координат и времени, то справедливы соотношения

П оэтому:

С ледовательно сумма

является полным дифференциалом частной производной потенциала скорости по времени, т.е.

Т аким образом, сумма уравнений Эйлера в проекциях запишется следующим образом:

Е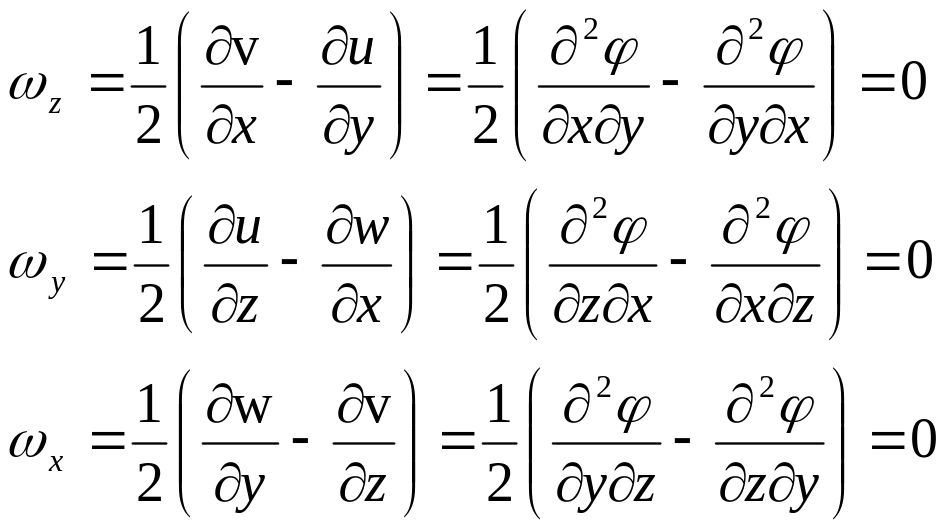 сли существует потенциал скорости, то компоненты вращательного движения тождественно равны нулю. Действительно:

П

(156)

оэтому сумма уравнений Эйлера в проекциях для безвихревого движения имеет вид:

Интегралом последнего уравнения является интеграл Коши -Лагранжа:

Постоянная интегрирования, зависящая от времени, постоянна для всей области течения и определяется из начальных условий в виде функции времени.

Е

(157)

сли течение является установившимся, то d /dt = 0, а сумма уравнений Эйлера в проекциях имеет вид:

Последнее уравнение справедливо как для вихревых, так и безвихревых течений. При этом, если правая часть уравнения равна нулю, то интеграл называется уравнением Бернулли:

Е сли массовые силы представлены только силами тяжести, действующими в направлении оси Z, то интеграл Бернулли имеет вид:

(158)

В

(159)

дифференциальной форме уравнение Бернулли записывается следующим образом:

П ри отсутствии массовых сил дифференциальное уравнение Бернулли описывает энергоизолированное установившееся движение идеальной жидкости. Интеграл этого уравнения для несжимаемой жидкости есть:

В случае сжимаемой жидкости интеграл дифференциального уравнения Бернулли для рассматриваемого случая имеет вид:

Правая часть уравнения (157) может быть равна нулю в следующих случаях.

1. стационарное безвихревое течение: _x = _y = _z = 0. Постоянная интегрирования одинакова для всей области течения (например, это давление торможения, одинаковое для всех струек тока несжимаемой жидкости)