
- •Игнатьев в.К.
- •Оглавление
- •Тема 1. Колебательные системы 7
- •Тема 2. Консервативные системы с одной степенью свободы Вопрос 4 17
- •Тема 3. Свободные колебания в диссипативных системах с одной степенью свободы Вопрос 6 24
- •Вопрос 7 26
- •Тема 4. Вынужденные колебания в системе с одной степенью свободы Вопрос 9 31
- •Тема 5. Параметрические системы с одной степенью свободы 40
- •Тема 6. Автоколебательные системы с одной степенью свободы 45
- •Тема 7. Колебательные системы с двумя степенями свободы 58
- •Тема 8. Колебания в линейных системах со многими степенями свободы 74
- •Тема 9. Колебания в распределённых системах. 86
- •Введение
- •Тема 1. Колебательные системы
- •1.1. Классификация колебательных систем
- •1.2. Уравнения линейных дискретных колебательных систем Вопрос 1
- •1.3. Автономные системы, символические уравнения Вопрос 2
- •1.4. Неавтономные системы, параметрический генератор
- •1.5. Уравнение Лагранжа для колебательных систем Вопрос 3
- •1.6. Фазовое пространство, представление движения
- •Тема 2. Консервативные системы с одной степенью свободы Вопрос 4
- •2.1. Колебания математического маятника
- •2.2. Метод последовательных приближений
- •2.3. Свободные колебания в резонансном контуре с нелинейной ёмкостью без затухания Вопрос 5
- •Тема 3. Свободные колебания в диссипативных системах с одной степенью свободы Вопрос 6
- •3.1. Линейный контур с затуханием
- •3.2. Метод медленно меняющихся амплитуд, укороченные уравнения Вопрос 7
- •3.3. Применение метода мма к колебательным системам Вопрос 8
- •Тема 4. Вынужденные колебания в системе с одной степенью свободы Вопрос 9
- •4.1. Вынужденные колебания в линейной системе при гармоническом воздействии
- •4.2. Вынужденные колебания в консервативной нелинейной системе при гармоническом силовом воздействии, гармонический баланс Вопрос 10
- •4.3. Генерация высших гармоник Вопрос 11
- •4.4. Метод мма для колебательных систем с малыми нелинейностями и потерями при гармоническом силовом воздействии
- •Тема 5. Параметрические системы с одной степенью свободы
- •5.1. Параметрическое воздействие на колебательный контур, передача энергии
- •5.2. Параметрические генераторы и усилители
- •Тема 6. Автоколебательные системы с одной степенью свободы
- •6.1. Классификация автоколебательных систем
- •6.2. Автоколебательные системы томпсоновского типа
- •6.3. Инерциальная нелинейность, стабилизация амплитуды
- •6.4. Автоколебательные системы с внешним воздействием, синхронизация колебаний
- •Тема 7. Колебательные системы с двумя степенями свободы
- •7.1. Парциальные системы и частоты, нормальные координаты и частоты
- •7.2. Вынужденные колебания в системе с двумя степенями свободы
- •7.3. Двухконтурный параметрический усилитель
- •7.4. Двухконтурный автогенератор
- •7.5. Затягивание колебаний
- •7.6. Синхронизация генераторов, метод Хохлова
- •Тема 8. Колебания в линейных системах со многими степенями свободы
- •8.1. Собственные колебания в консервативных системах
- •8.2. Ортогональность нормальных колебаний и экстремальные свойства собственных частот
- •8.3. Вынужденные колебания в системе с n степенями свободы
- •8.4. Колебания в однородных цепочках
- •8.5. Параметрические системы, соотношения Менли-Роу
- •Тема 9. Колебания в распределённых системах.
- •9.1. Телеграфные уравнения, волновое уравнение
- •9.2. Собственные колебания распределённых систем конечной длины
- •9.3. Вынужденные колебания в распределённых системах
- •9.4. Лазер как автогенератор
- •Список рекомендуемой литературы1
2.1. Колебания математического маятника
Это классическая механическая система, и поэтому её удобно рассматривать с помощью формализма Лагранжа. Поскольку система первого порядка и консервативна, то уравнение Лагранжа (1.32) для такой системы имеет простой вид:
|
(2.2) |
Для него есть первый интеграл движения энергия:
|
(2.3) |
Продифференцируем (2.3) по времени, воспользовавшись равенством (2.2),
 .
.
Таким образом, Н = const. Теперь покажем консервативность системы, описываемой уравнением (2.1). Найдём для этой системы уравнение фазовой траектории из общего уравнения (1.38)
|
(2.4) |
Это уравнение легко интегрируется:
 .
.
Получается, что на фазовой траектории сохраняется полная энергия как сумма потенциальной и кинетической (фазовая траектория есть линия постоянной энергии). Следовательно, другая форма записи фазовой траектории имеет вид:
|
(2.5) |
Меняя величину этой константы, мы будем получать разные фазовые траектории.
Рассмотрим особые точки, одной из которых является положение равновесия. Пусть q0 есть положение равновесия. Это означает, что, если мы привели систему в состояние равновесия с нулевой скоростью, то она там и останется. Судя по уравнению (2.1), если бы действовала сила, система бы вышла из положения равновесия. Положение равновесия должно отвечать нулевой силе, следовательно, экстремуму потенциальной энергии. Разложим в окрестности точки q0 потенциальную энергию в ряд Тейлора, учтя, что первая производная от потенциальной энергии равна нулю:
![]() .
.
Обозначим значение потенциальной энергии в точке равновесия как какое-то Н0, т. е. V(q0) = H0. Так как в этой точке кинетическая энергия равна нулю (y = 0), то потенциальная энергия в точке равновесия совпадает с полной энергией, которая сохраняется на всей фазовой траектории. Введём новую переменную x = q q0 отклонение от точки равновесия. Для малых отклонений пренебрегаем старшими степенями, и тогда (2.5) принимает вид:
|
(2.6) |
Если > 0, что означает минимум потенциальной энергии, уравнение (2.6) описывает замкнутую кривую (эллипс); если < 0, т. е. точка равновесия соответствует максимуму потенциальной энергии, то (2.6) описывает разомкнутую кривую (гиперболу), поэтому это положение равновесия называется безразличным равновесием (любая точка будет являться точкой равновесия, например, поверхность стола).
Что значит замкнутая кривая? При движении наша система движется всё время по одному и тому же контуру, это означает повторяемость движения, т. е. периодический колебательный процесс. Минимуму потенциальной энергии соответствуют периодические колебания вокруг этого минимума, а максимуму какие-то инфинитные движения.
Конкретизируем эту задачу по отношению к математическому маятнику длиной l. Его уравнение (выберем в качестве обобщённой координаты x угол отклонения от вертикали):
|
(2.7) |
Тогда уравнение фазовой траектории имеет вид:
![]() ,
,
а уравнение для потенциальной энергии:
![]() ,
,
и, наконец, уравнение (2.5) для полной энергии примет вид:
|
(2.8) |
Из (2.8) следует, что
если
![]() ,
то всюду на фазовой траектории y
отлично от нуля, т. е. движение не
ограничено или фазовые траектории
незамкнуты. Если
,
то всюду на фазовой траектории y
отлично от нуля, т. е. движение не
ограничено или фазовые траектории
незамкнуты. Если
![]() ,
то существует координата x0,
при которой переменная y
обращается в нуль: y(x0) = 0;
дальше точки x0
движения происходить не может, и система
просто повернёт назад, т. е. второй случай
описывает ограниченные повторяющиеся
движения (колебания). После таких
качественных исследований попробуем
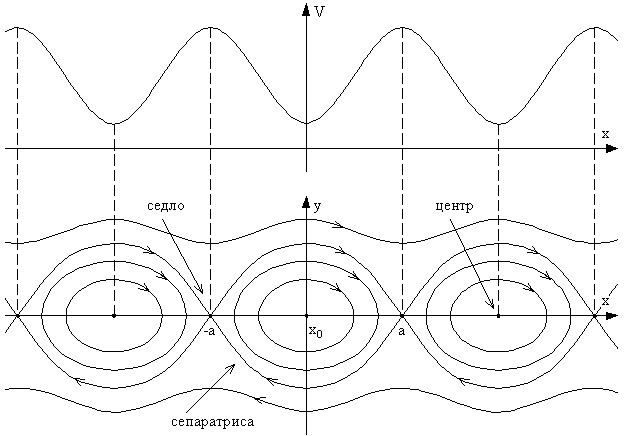
представить всё графически (рис. 18).
Здесь изображены два графика: зависимость
потенциальной энергии от координаты и
зависимость скорости от координаты.
Изменение величин происходит в том
направлении, в каком указывают стрелки.
Точка, которой соответствует минимум
потенциальной энергии (устойчивое
положение равновесия), и вокруг которой
накручены кривые, называется центр.
Точка, которой соответствует максимум
потенциальной энергии (неустойчивое
равновесие), называется седло.
Кривая, которая разделяет область
финитного движения (эллиптические
траектории) и инфинитного движения
(гиперболические траектории) и проходит
через сёдла, называется сепаратриса.
,
то существует координата x0,
при которой переменная y
обращается в нуль: y(x0) = 0;
дальше точки x0
движения происходить не может, и система
просто повернёт назад, т. е. второй случай
описывает ограниченные повторяющиеся
движения (колебания). После таких
качественных исследований попробуем
представить всё графически (рис. 18).
Здесь изображены два графика: зависимость
потенциальной энергии от координаты и
зависимость скорости от координаты.
Изменение величин происходит в том
направлении, в каком указывают стрелки.
Точка, которой соответствует минимум
потенциальной энергии (устойчивое
положение равновесия), и вокруг которой
накручены кривые, называется центр.
Точка, которой соответствует максимум
потенциальной энергии (неустойчивое
равновесие), называется седло.
Кривая, которая разделяет область
финитного движения (эллиптические
траектории) и инфинитного движения
(гиперболические траектории) и проходит
через сёдла, называется сепаратриса.
Рис. 18. Фазовый портрет маятника. |
Мы сказали, что эллиптическим траекториям отвечает периодическое движение. Найдём период колебаний. Для этого уравнение (2.8) перепишем в виде:
![]() ,
,
и проинтегрируем
 .
.
где t это время движения между точками x1 и x2. Период это удвоенное время прохождения между двумя крайними точками (в этих точках кинетическая энергия обращается в нуль). Формально обозначим амплитуду колебаний как a; положению равновесия пусть отвечает точка x0 = 0. Так как в точке а кинетическая энергия равна нулю, а энергия Н константа, то она должна принять вид:
![]() .
.
Тогда мы можем утверждать, что
|
(2.9) |
Как видно из формулы (2.9), период колебаний зависит от амплитуды. Это явление, зависимость периода колебаний от амплитуды, называется неизохронностью колебаний. Неизохронность всегда является следствием нелинейности системы.

 .
.