18,19 Потенциальное силовое поле. Потенциальная энергия.

Силовое поле - часть пространства, в каждой точке которого на помещенную в ней материальную точку действует сила, зависящая только от положения этой точки. Потенциальное силовое поле - это стационарное (не изменяющееся во времени) поле, работа сил которого не зависит от формы траектории точки, а только от ее начального и конечного положений. Силовая функция потенциального поля - такая функция, что: . Потенциальные силы - силы потенциального поля. Элементарная работа потенциальной силы равна полному дифференциалу силовой функции:

.

Элементарная работа силы потенциального поля равна полному дифференциалу силовой функции:

Полная работа потенциальной силы равна разности значений силовой функции в начальном и конечном положении точки. На замкнутом перемещении равна нулю.

Потенциальная энергия - величина, отличающаяся от силовой функции, взятой с отрицательным знаком, на постоянную величину - нулевое значение силовой функции. A = u₀ - u = П. Проекции потенциальной силы, действующей на материальную точку равны взятым с отрицательным знаком частным производным от потенциальной энергии по соответствующим координатам: .

Эквипотенциальная поверхность - поверхность равного потенциала, единственная для каждой точки поля - ГМТ с постоянным значением потенциальной энергии.

Консервативная система (от лат. conservo — сохраняю), механическая система, для которой имеет место закон сохранения механической энергии, т. е. сумма кинетической энергии Т и потенциальной энергии П системы постоянна: Т + П = const.

Работа силы на конечном перемещении точки в потенциальном силовом поле. Потенциальная энергия.

Работа силы потенциального поля при перемещении точки из положения М1 в положение М2. (рис. 23).

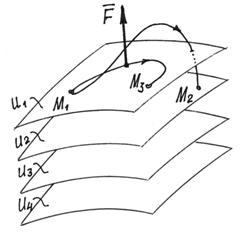Рис.23

Элементарная работа,

Это есть полный дифференциал силовой функции.

Работа на конечном перемещении

где u2 и u1 – значения силовой функции в точках М2 и М1.

Работа силы потенциального поля не зависит от траектории движения точки, а определяется лишь значениями силовой функции в начальном и конечном положениях точки. Если точка вернется в начальное положение, работа силы будет равна нулю. Работа окажется равной нулю и при переходе в другую точку М3, если там значение силовой функции будет такое же, как и в начальном положении. Точки с одинаковыми значениями силовой функции будут образовывать целую поверхность. силовое поле – это слоеное пространство, состоящее из таких поверхностей (рис. 23). Эти поверхности называются поверхностями уровня или эквипотенциальными поверхностями. Уравнения их: u(x, y, z)=C (C – постоянная, равная значению u в точках этой поверхности). А силовую функцию называют, соответственно, потенциалом поля. Эквипотенциальные поверхности не пересекаются. Иначе существовали бы точки поля с неопределенным потенциалом. Поскольку, при перемещении точки по эквипотенциальной поверхности работа силы равна нулю, то вектор силы перпендикулярен поверхности. Работа, которую совершит сила при переходе точки из определенного места М на нулевую поверхность, называют потенциальной энергией точки в этом определенном месте М:

(8)

Заметим, что потенциальная энергия в одной и той же точке поля зависит от выбора нулевой поверхности. По (8) силовая функция . Поэтому проекции силы на декартовы оси, по (6), так как ,

; ; (9)и вектор силы .