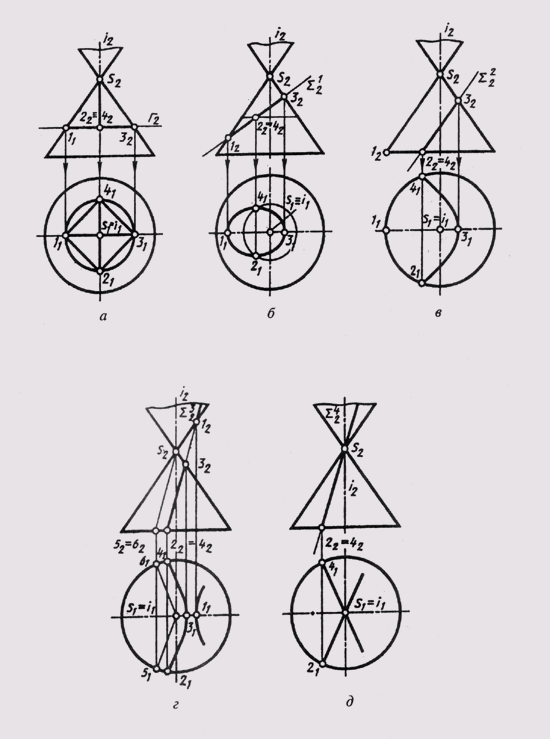Вопрос 22.
Способы задания поверхности на чертеже. Построение проекций точек, линий, принадлежащих
поверхности.
Для задания поверхности могут быть использованы три основных способа:
А
налитическийКаркасный
Кинематический
Аналитический способ
При аналитическом способе задания поверхность рассматривается как множество точек, координаты которых удовлетворяют заданному уравнению.
В этом случае поверхность задается уравнением.
Каркасный способ
При каркасном способе задания поверхность рассматривается как совокупность достаточно плотной сети линий, определяющих поверхность.
Эта сеть называется каркасом.
Кинематический способ
При кинематическом способе задания поверхность рассматривается как совокупность всех положений движущейся линии.
Этот способ задания поверхности является предпочтительным в инженерной графике.
В инженерной графике поверхность рассматривают как множество всех последовательных положений движущейся линии.
Принадлежность точки поверхности Точка принадлежит поверхности, если она принадлежит какой-либо линии поверхности. Для построения точек, принадлежащих проецирующей поверхности, удобно воспользоваться вырожденной проекцией. Для построения недостающих проекций линии, принадлежащей кривой поверхности, надо
Если линия пересекает
то необходимо, обязательно, построить проекции этих точек, они будут служить границей видимости для соответствующих проекций линии.
|
|
Вопрос 23.
Сечение поверхности вращения плоскостью.
В случае пересечения цилиндрической поверхности вращения плоскостью могут быть получены следующие линии (рис. 124, б):
На плоскость П1, перпендикулярную оси вращения поверхности, окружность и эллипс на поверхности цилиндра проецируются в окружность, совпадающую с проекцией всей поверхности.
|
При пересечении конической поверхности вращения плоскостью могут быть получены следующие линии (рис. 125, а — д): 1)окружность, если секущая плоскость Г перпендикулярна оси вращения (а); 2)эллипс, если секущая плоскость Sum1 пересекает все образующие поверхности (б); 3)парабола, если секущая плоскость (Sum2) параллельна только одной образующей (S— 1) поверхности (в); 4)гипербола, если секущая плоскость (Sum3) параллельна двум образующим (S—5 и 5—6) поверхности (г); 5)две образующие (прямые), если секущая плоскость (Sum4) проходит через вершину S поверхности (д). Проекции кривых линий сечений
|
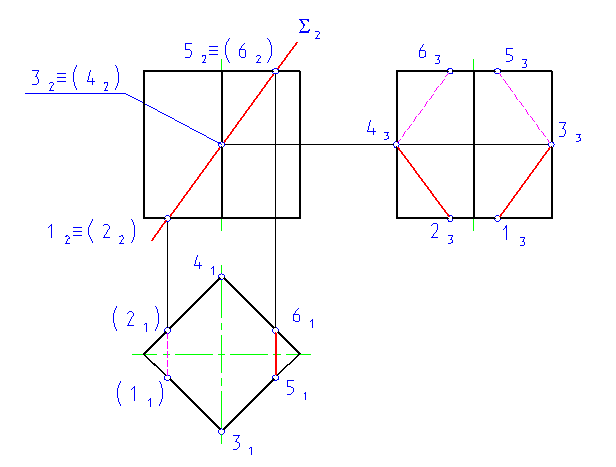
При пересечении сферы плоскостью всегда получается окружность. Если секущая плоскость параллельна какой-либо плоскости проекций, то на эту плоскость окружность сечения проецируется без искажения (рис. 126, а). Если секущая плоскость занимает проецирующее положение, то на плоскости проекций, которой секущая плоскость перпендикулярна (рис. 126, б—на фронтальной), окружность сечения изображается отрезком прямой (12—42), длина которого равна диаметру окружности, а на другой плоскости — эллипсом, большая ось которого (51—61) равна диаметру окружности сечения |
|
