Дифференциал функции – определение, геометрический смысл. Доказать инвариантность формы дифференциала первого порядка.
Дифференциалом функции y=f(x) в точке называют главную линейную, относительно приращения аргумента, часть полного приращения функции в данной точке.
Инвариантность формы первого дифференциала.
;
,
где Х – независимая переменная.
Билет №11. Доказать второе достаточное условие экстремума.
Пусть ф-ция определена и имеет в окрестности точки с производную до n-го порядка включительно, причем в самой точке с все производные до (n-1)-го порядка включительно равны 0, а n-ная производная в точке С отлична от нуля. Если n – четное, тогда С – точка локального экстремума, в частности, если , то x=c –локальный минимум, если , то x=c –локальный максимум.
Доказательство: Запишем формулу Тейлора
с остаточным членом в форме Пеано с
центром в точке С.
,
где
-б.м.ф.
при
.
Пусть n – четное, тогда
не меняет знак при переходе через С.
в которой функция сохраняет знак своего
предела.
,
.
.
,
если
-
точка локального экстремума.
Доказать теорему о пределе произведения функций.
Пусть
и
при
имеют конечные пределы равные A
и B соответственно, тогда
Дано:
Доказательство:
,
,
Билет №12. Доказать достаточное условие выпуклости графика функции.
Пусть
определена и дважды дифференцируема
на
.
Для того, чтобы график функции имел
направление выпуклости вниз (вверх)
достаточно, чтобы
была неотрицательная (неположительная)
на
.
Доказательство:
Дано:
Доказать: - выпуклость вниз на .
Пусть
.
Уравнение касательной:
,
где
,
если
,
,
если
,
,
т.к.
график функции
на
лежит не ниже касательной
выпуклость вниз на
.
Доказать теорему о знакопостоянстве функции, имеющей отличный от нуля предел.
Если
,
то существует окрестность точки а, в
которой
и знак
совпадает со знаком значения b.
Доказательство: по условию
,
т.е.
,
или
справедливы неравенства
.
Возьмём за
число
.
Тогда
,
,
являются числами одного знака.
Следовательно, в силу неравенства
,
и имеет знак числа b в
указанной
-окрестности
точки а.
Билет №13. Необходимое и достаточное условие существования точки перегиба графика функции. Доказать необходимое условие.
Пусть функция
определена и дважды непрерывно-дифференцируема
в окрестности точки С. Для того, чтобы
(с,
),
была точкой перегиба графика функции
,
необходимо чтобы
.
Доказательство:
Дано: (с, ) – точка перегиба.
Доказать: .
- это значит, согласно свойству
непрерывности, что функция обладает
знакопостоянством.
,
т.е. в этой окрестности график функции
имеет одинаковые направления выпуклости
слева и справа от точки С, что противоречит
определению точки перегиба
в точке С
.
Доказать теоремы об эквивалентных бесконечно малых.
Теорема. Для того, чтобы б.м.ф.
и
при
были эквивалентными, при
необходимо и достаточно, чтобы
,
.
Доказательство. Необходимость.
Дано.
Доказать, что (
.
Достаточность. Дано.
Доказательство.
.
Рассмотрим сумму конечного числа б.м.ф.
,
где
-
б.м.ф. при
.
Пусть
,
k=2,3,….n тогда
-
главная часть б.м.ф.
Билет №14.
Доказать теорему Коши.
Пусть функции f(x)
и g(x): 1)
определены и непрерывна на [a,b];
2) дифференцируемы на интервале (a,b);
3)
тогда
.
Доказательство:
Вводим вспомогательную функцию
.
Эта функция удовлетворяет всем условиям
теоремы Ролля: 1)
непрерывна на [a,b];
2)
дифференцируема на (a,b);
3)
.
(по теор. Ролля).
.
.
Вывести формулу для производной сложной функции.
Пусть функция
,
дифф. В точке t=t0,
а функция
-
дифференцируема в точке
,
тогда функция
дифференцируема в точке t=t0,
причем
.
Док-во (должны доказать, что
).
Имеем, что
.
.
.
Билет №15.
Доказать достаточное условие возрастания дифференцируемой функции.
Для того, чтобы функция
,
определённая и дифференцируемая на
,
возрастала на
,
достаточно, чтобы
на
.
Доказательство:
Дано:
Доказать: - возрастает на
- определена
- дифференцируемая.
Согласно т. Лагранжа
,
т.к.
,
- возрастает на
.
Длина дуги плоской кривой. Производная и дифференциал длины дуги плоской кривой.
Рассмотрим в XOY плоскую кривую Г.
;
-
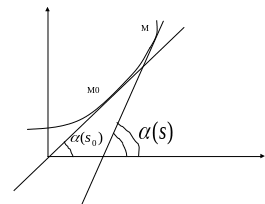
Средняя кривизна кривой Г. Кривизной
кривой Г в точке
называют предел (если он существует)
средней коивизны при
.
;
;
Если
,
то полагают
Билет №16-1.
Формула Тейлора с остаточным членом в форме Пеано, Лагранджа.
Теорема. Пусть ф-ция F(x) определена в и имеет в производные до (n+1)-го порядка включительно. Пусть x – произвольное значение аргумента ф-ции из , тогда для произвольного значения P, p>0 , расположенная между a и x, такие что справедлива следующая формула: . . Формула называется формулой Тейлора с центром в точке a; - остаточный член в формуле Тейлора в общем виде.
эта функция – многочлен степени n – многочлен Тейлора с центром в точке а.
Обозначим . Рассмотрим вспомогательную функцию .
, где Покажем, что на [a;x] удовлетворяет всем условиям теоремы Ролля:
непрерывность на [a;x];
дифференцируема на (a;x);
; ; ;
Теорема. Остаточный член в форме Тейлора представляет собой б. м. более высокого порядка малости, чем при . , .
Доказать:
; =0; ; n раз применяем пр. Б-Л.=
Такую запись остаточного члена называют ост. чл. в форме Пеано: .
Рассмотрим другие формы записи остаточного члена. ,
1) p=n+1, тогда - остаточный член в форме Лагранжа.
2) p=1 – в форме Коши: Число в формуле Лагранжа и формуле Коши разные, т. к. зависят от P. Остаточный член в форме Лагранжа и Коши представляют собой погрешность, которую мы получаем, заменяя функцию f(x) ее многочленом Тейлора. Если нас интересует порядок малости такой замены при , то он совпадает с порядком малости остаточного члена в форме Пеано.
Оценка остаточного члена в форме Лагранжа.
Пусть функция имеет производную любого порядка в и эти производные ограничены одной и той же константой M. ;
Билет №16-2.
Доказать непрерывность функций и
1)
Зададим приращение аргумента функции в точке X:
Здесь использовано неравенство
.
Итак,
. Тогда
, т.е.
функция
непрерывна
в точке X,
а т.к. точка X
принадлежит R
, т.е. произвольна, то можна сказать, что
функция
непрерывна на всей числовой оси.
2) ыв
Зададим приращение аргумента функции в точке X:
,
-
непрерывная функция.
Билет №17.
Доказать первое достаточное условие экстремума функции.
Пусть функция определена и дифференцируема в окрестности точки С. Для того, чтобы точка С являлась точкой локального экстремума, достаточно чтобы при переходе значений аргумента через точку С производная функции меняла знак с “+” на “-” – локальный максимум, с “-” на “+” – локальный минимум.
Доказательство: Рассмотрим точку X из указанной окрестности, тогда:
на - непрерывна.
на - дифференцируема.
По т. Лагранжа , где , т.к. , то
на : где ,
Непрерывность сложной функции.
Пусть
- непрерывна в точке x=a,
а функция
- непрерывна в точке b=f(a),
тогда сложная функция z=g(f(x))
– непрерывна в точке x=a.
Доказательство: Т.к g(y)
– непрерывна в точке y=b,
то
,
т.к. y=f(x)
– непрерывна в точке x=a,
то
.
Замечание:
Билет №18.
Теорема о связи дифференцируемости и непрерывности.
Для того чтобы функция была дифференцируема в точке, необходимо, чтобы она была непрерывной в этой точке.
Дано: - дифференцируема в точке.
Доказать: - непрерывна в точке.
,
где
- б.м.ф. при
.
- непрерывна в заданной точке.
Доказать теорему о пределе промежуточной функции.
Пусть функции
и
имеет конечный предел А при
и пусть
тогда
Доказательство:
,
,
Рассмотрим
,
начиная с некоторого номера N
и
,
будут одинакого выполняться
.
Значит,
Билет №19.
Доказать теорему Лагранжа.
Пусть функция .
Определена и непрерывна на отрезке .
Дифференцируема на интервале .
Тогда существует из интервала .
Доказательство: Рассмотрим вспомогательную функцию , где - константа.
Она непрерывна на
дифференцируема на .
Все условия теоремы Ролля выполняются существует из
Дифференциал функции – определение, геометрический смысл. Доказать инвариантность формы дифференциала первого порядка.
Дифференциалом функции y=f(x) в точке называют главную линейную, относительно приращения аргумента, часть полного приращения функции в данной точке.
Инвариантность формы первого дифференциала.
; , где Х - независимая переменная.
Билет №20.
Доказать теоремы Ролля и Ферма.
Пусть дана функция .