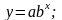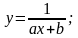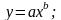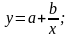9 Определение вида и параметров эмпирической зависимости
Задание 17.
Дана таблица экспериментальных данных:
-
x
0,5
0,7
1
1,5
3
3,5
4
4,5
y
0,1111
0,16279
0,25000
0,42857
1,49996
2,33330
4,00010
7,99995
Руководство к выполнению Задания 17.
Построить график по заданным точкам.
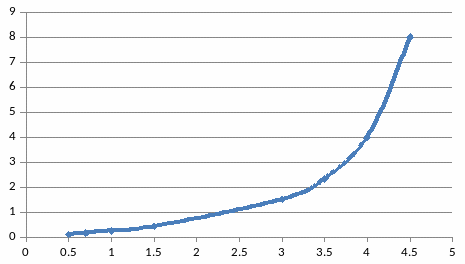
Рисунок 106
2. Установить вид зависимости.
Вид зависимости выбирается из числа следующих семи зависимостей:
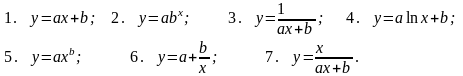
Для определения вида зависимости вычислим средние величины:
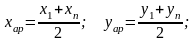
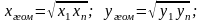
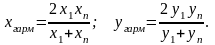
Для данной таблицы значений:
; 
;
;
;
;
.
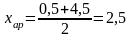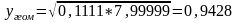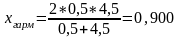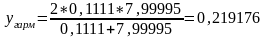Определим значения
,
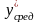соответствующие каждому
.
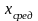Правило: если
значение
совпадает со значением
из таблицы данных, то
,
соответствующее этому
,
равно
из таблицы данных.
Для
,
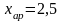не совпадающего ни с каким
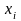в таблице исходных данных, значение
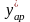вычисляется по формуле линейной
интерполяции
.
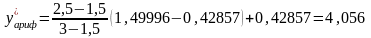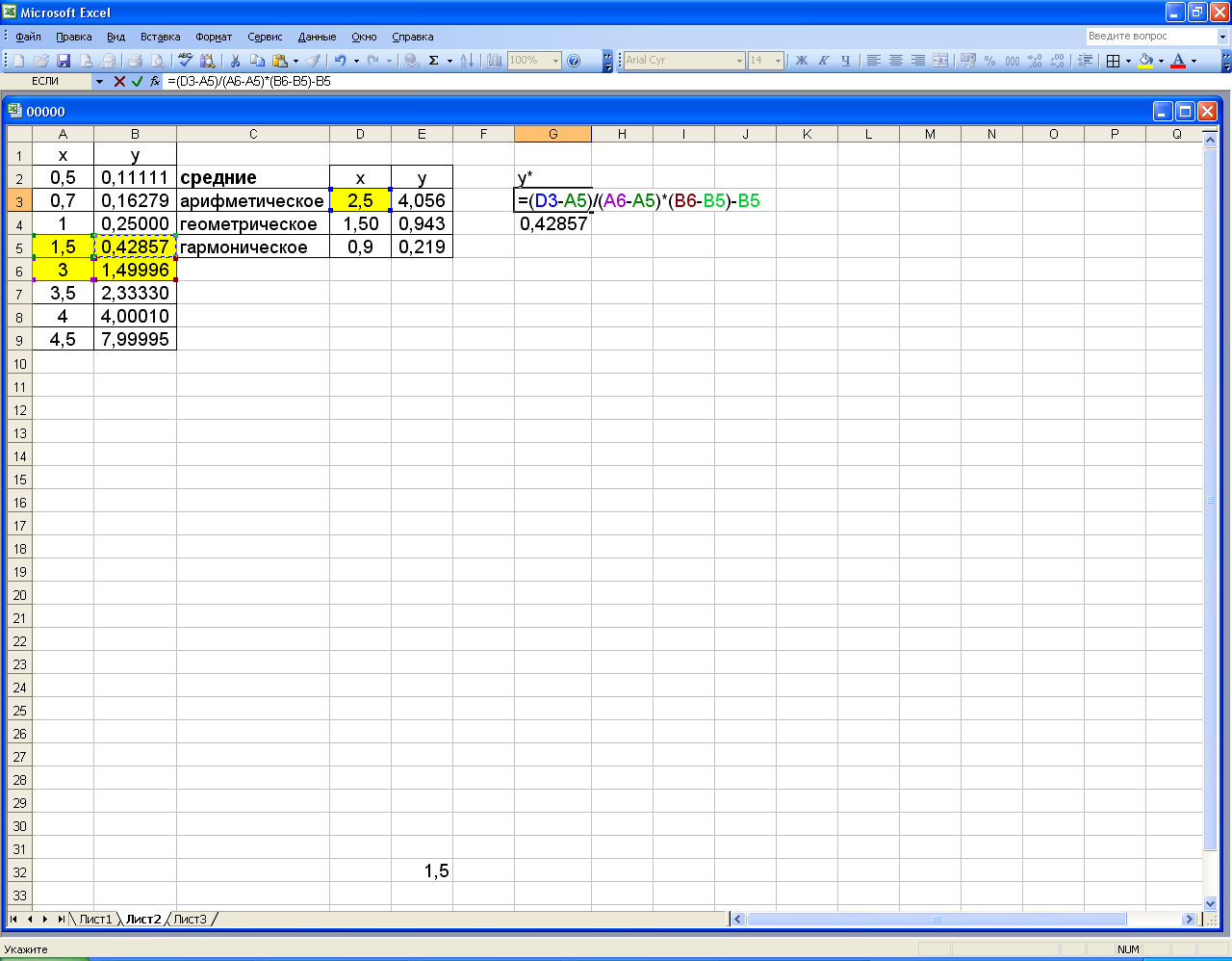
Рисунок 107
Так как
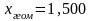равно
значению
,
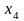то и
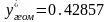равно значению
.
Значение
,
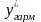соответствующее
,
определяем согласно Рисунку 107 по формуле
линейной интерполяции:
.
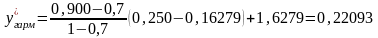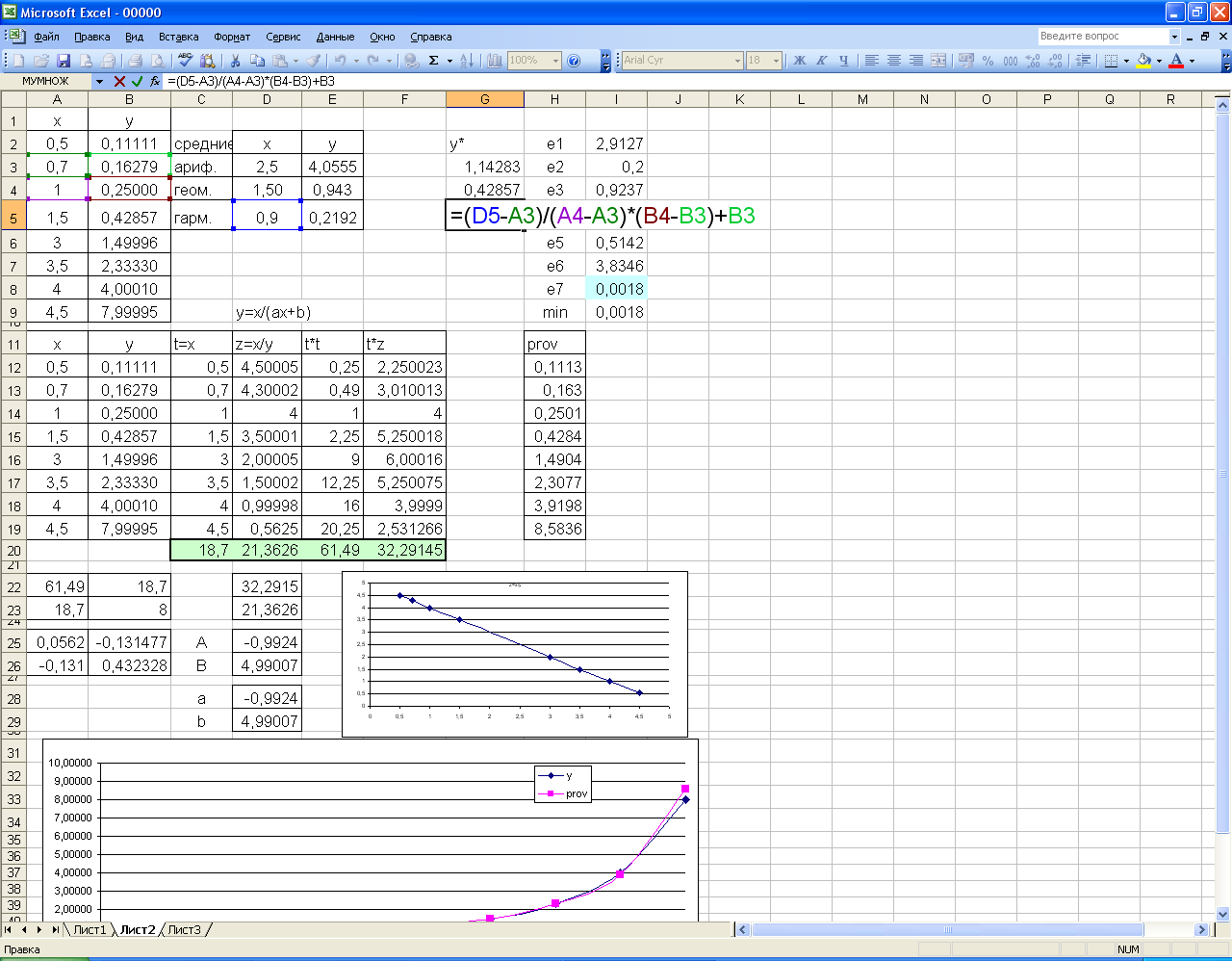
Рисунок 108
Определим погрешности по следующим формулам:
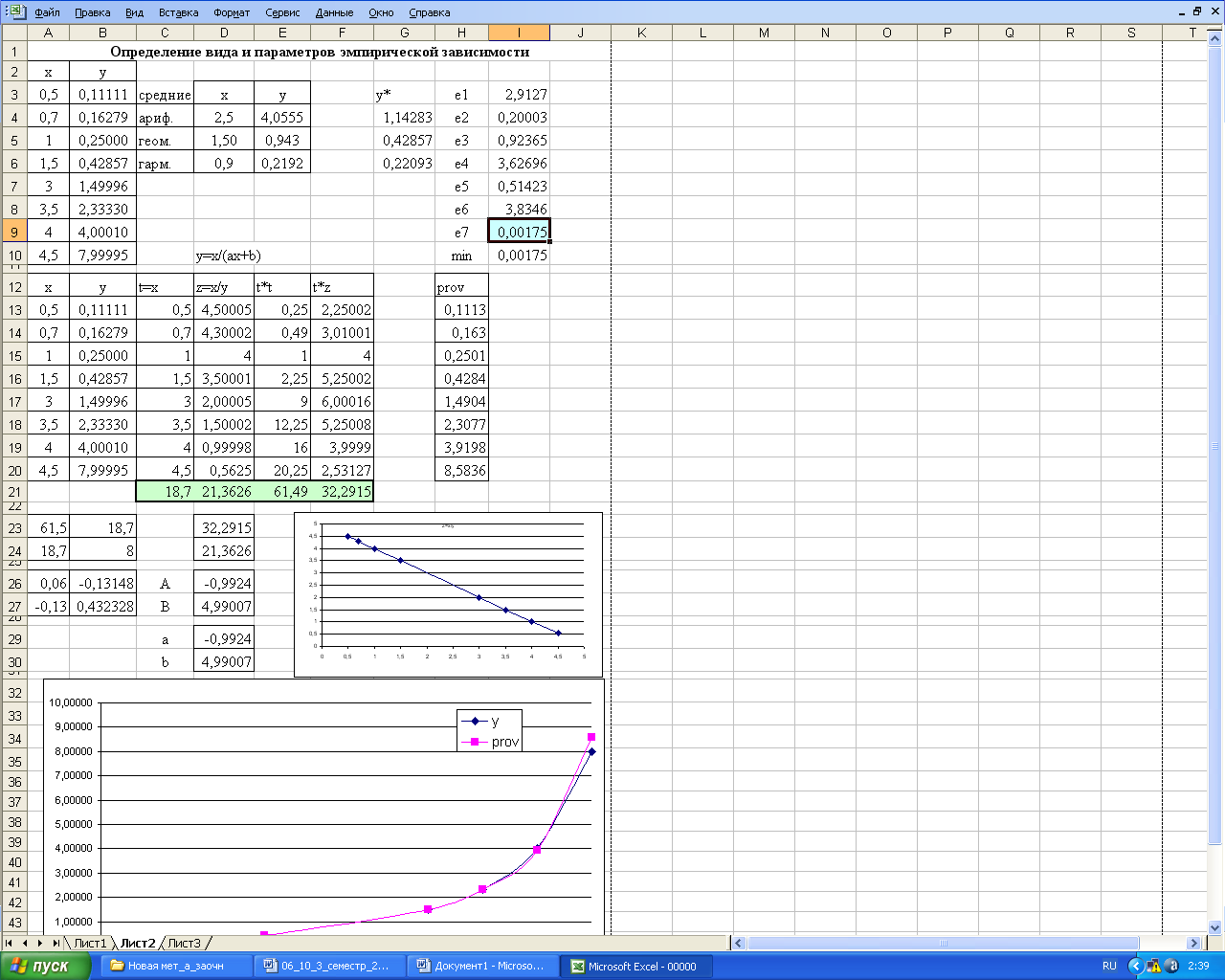
Рисунок 109
Самая малая
погрешность
.
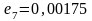В списке зависимостей под номером 7 -
зависимость
.
3. Определение коэффициентов полученной зависимости.
Для определения коэффициентов исходной зависимости преобразуем её к линейному виду Z=At+B.
Зависимость не
обязательно вида
,
рассмотрим переход от любой из
предложенных функций
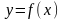к линейной зависимости Z=At+B.
№ |
Функция |
t |
Z |
Обратный переход |
Вывод формул перехода |
|
|
y=ax+b |
x |
y |
a=A b=B |
|
|
|
|
x |
ln y |
a=exp(B),b=exp(A) |
ln y =ln a + x ln b |
|
|
|
x |
1 / y |
a=A b=B |
|
|
|
y=alnx+b |
ln x |
y |
a=A b=B |
|
|
|
|
ln x |
ln y |
a=exp(B) b=A |
ln y =ln a + b ln x |
|
|
|
x |
x y |
a=A b=B |
|
|
|
|
x |
x / y |
a=A b=B |
|
По формулам для функции получаем таблицу значений:
x |
y |
t=x |
z=x/y |
0,5 |
0,11111 |
0,5 |
4,50005 |
0,7 |
0,16279 |
0,7 |
4,30002 |
1 |
0,25000 |
1 |
4 |
1,5 |
0,42857 |
1,5 |
3,50001 |
3 |
1,49996 |
3 |
2,00005 |
3,5 |
2,33330 |
3,5 |
1,50002 |
4 |
4,00010 |
4 |
0,99998 |
4,5 |
7,99995 |
4,5 |
0,5625 |
Рисунок 110
Для проверки правильности перехода к линейной зависимости необходимо построить график функции Z, если на графике будет прямая, значит функция Z определена верно.
Параметры A и B для функции Z определяются с помощью функции ЛИНЕЙН.
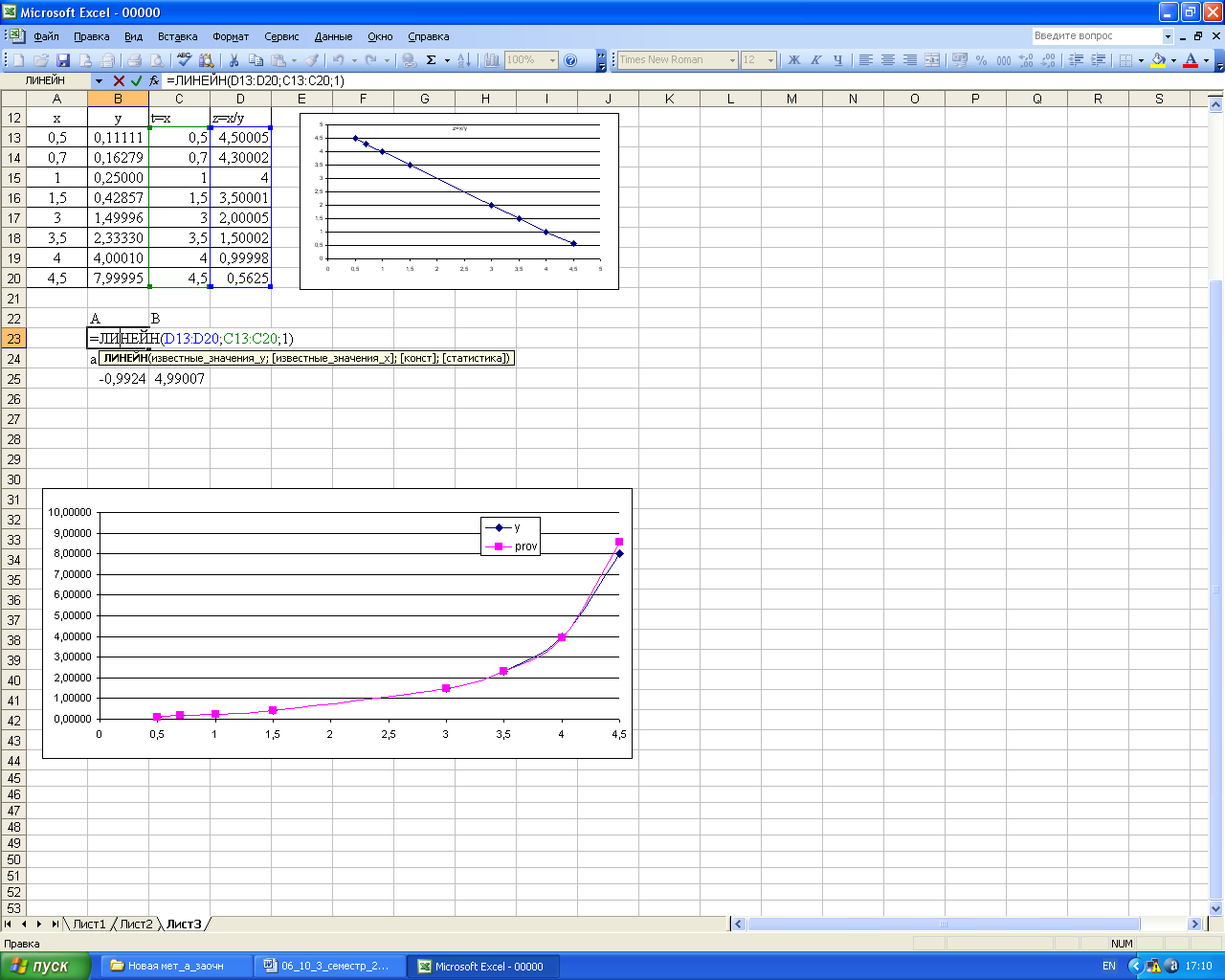
Рисунок 111
Параметры функции определяются из таблицы перехода от функции Y к функции Z.
Для проверки
полученного решения вычислим значения
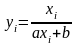и построим общий график.
Работа, выполненная в EXCEL, должна быть оформлена согласно Рисунку 112.
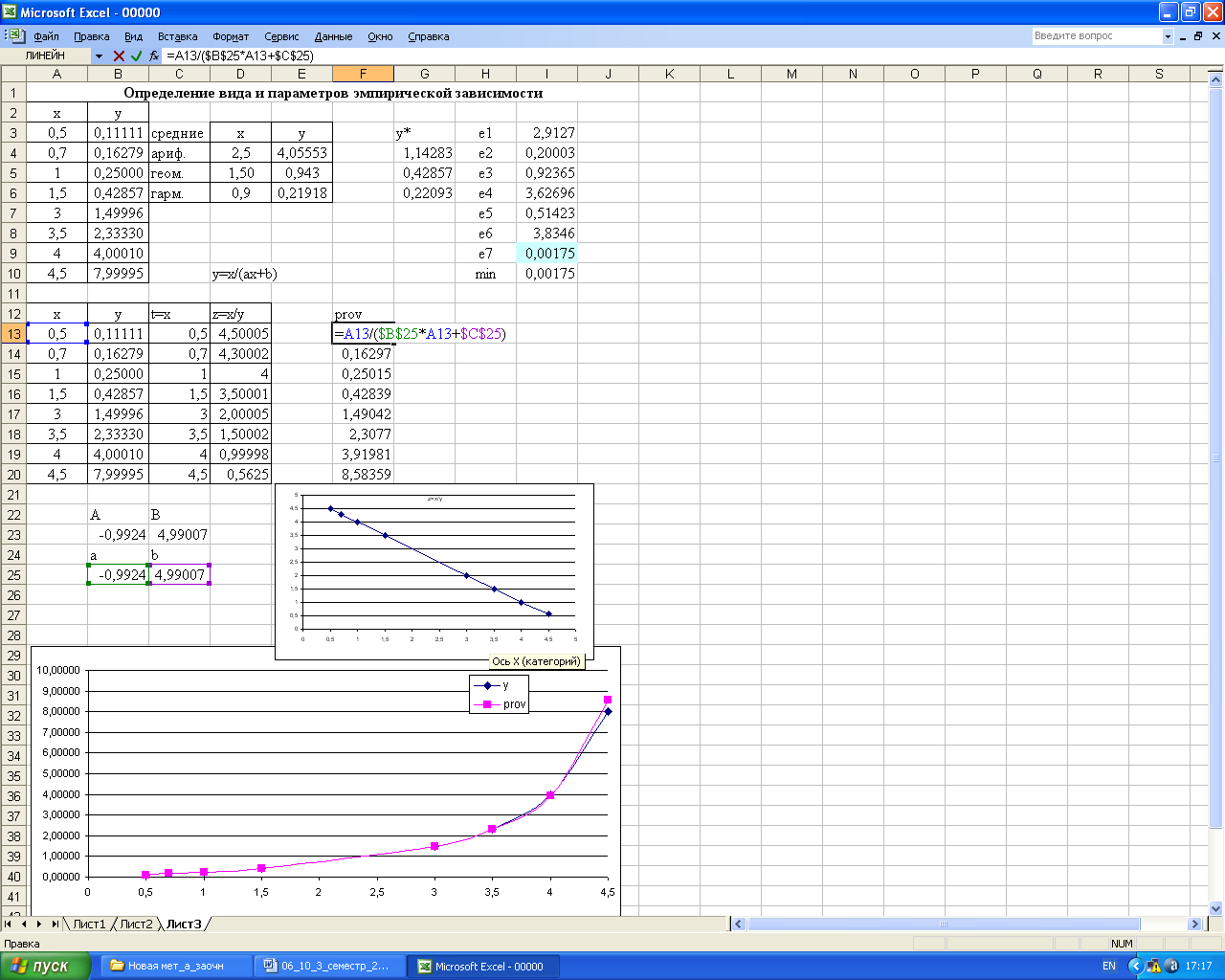
Рисунок 112