1.5. Автоматы Мура

Определение. Автоматом Мура называют набор А= (Х, Z, Q, F, G), в котором:

1) Х = (Х₁,Х₂,…,Х_N) – множество возможных входов,

2) Z = (Z₁,Z₂,…,Z_M) – множество возможных выходов,

3) Q = (Q₁,Q₂,…,Q_Р) – множество возможных внутренних состояний,

4) F : Q Z - функция выходов,

5) G : х q q - функция переходов.

Как следует из определения, отличие автомата Мура от автомата Мили заключается в том, что выход у него фор-мально не зависит от входа, а только от внутреннего со-стояния автомата. Однако в общем случае неявная зависи-мость выходов Z от входов Х присутствует, поскольку Z зависит от внутренних состояний Q, а Q - в свою очередь - от входов Х .

Пример 1. Наиболее распространенным автоматом Мура является автономный светофор, в котором переклю-чение цветов “красный – желтый – зеленый – желтый - …”

297

происходит независимо от внешних условий, а только в зависимости от предыдущего состояния.

Отметим, что в приведенном примере у автомата отсутствует вход.

Для задания автоматов Мура используют те же спосо-бы, что и для автоматов Мили. При этом на графе пере-ходов значения выходов проставляют внутри либо рядом с вершинами, обозначающими состояния автомата.

Пример 2. Построить граф переходов и таблицу со-стояний для автономного светофора.

Решение. Выходной информацией, выдаваемой устройст-вом, являются световые сигналы красного, зеленого и жел-того цвета. Обозначим их, соответственно, К,З,Ж. Внут-ренние состояния, соответствующие красному и зеленому цвету, обозначим через q_к и q_з. Поскольку желтый цвет дол-

жен зажигаться дважды при разных внутренних состояни-

ях, для него отводим два состояния: q_жк и q_жз, соответ-ствующие желтому цвету, включаемому после красного и после зеленого цветов. Искомый граф переходов имеет вид, показанный на Рис.5.10.

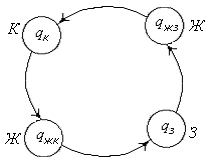
Рис.5.10

Таблица состояний имеет вид:

298

Qj (ti-1)	Z	Qj (ti)
q к	К	qжк
qжк	Ж	q з
q з	З	q жз
q жз	Ж	q к

Несмотря на то, что автоматы Мура являются частным случаем автоматов Мили (полученным при наложении дополнительных ограничений на функцию выходов), их потенциальные возможности совпадают. Это вытекает из следующего утверждения.

Теорема.

Для любого автомата Мили А = (Х,Z,Q,F,G) существу-ет эквивалентный ему автомат Мура А = (Х,Z,Q,F,G) .

Доказательство. Обозначим: Х=N, Z=M, Q=P.

Укажем способ построения эквивалентного автомата Мура. Множества входов и выходов его примем такими же, как и у исходного автомата Мили: Х =Х, Z =Z. Множество внутренних состояний построим состоящим из двух частей: Q= QQ^д, где Q - множество состояний автомата Мили, Q^д ={ Q^д_ij; i=1,…,P;j=1,…,N}– множество дополнительных состояний, Q^д=P N.

Определим функцию переходов автомата Мура G следующим способом:

а) на множестве Q (в момент времени t₁ )

G (Q_i,Х_j)= Q^д_ij;

б) на множестве Q^д (в моменты времени t₂, t₃ , …)

G (Q^д_ij ,Х_k)= Q^д_lk; где Q_l = G(Q_i ,Х_k) .

Таким образом, в момент времени t₁ происходит пере-ход из подмножества состояний Q (в котором задано на-чальное состояние автомата) в подмножество Q^д, где осуществляется его последующее функционирование. Ин-формация о текущем состоянии автомата Мили запоминает-

299

ся в первом индексе дополнительного состояния автомата Мура, информация о текущем входе – во втором индексе. За счет этого дополнительные состояния Q^д автомата Мура содержат полную информацию о внутреннем состоянии и входе автомата Мили в каждый момент времени.

Функция выходов автомата Мура может быть задана таким способом:

а) F(Q_i) - не определено, поскольку данные состояния при срабатывании F не достижимы (в момент времени t₁ проис-ходит переход из Q в Q^д и дальнейшая работа осуществ-ляется в данном подмножестве состояний);

б) F( Q^д_ij )= F ( Q_i, Х_j) .

Эквиваленность автоматов А и А следует из способа задания функций переходов и выходов F и G.

Пример 3. Построить автомат Мура, эквивалентный сокращенному автомату Мили, построенному в Примере 2 п.1.4.

Решение. Задаем множества входов, выходов и внутренних состояний:

Х = Х =(a, b); Z=Z=(x, y, z);

Q =QQ^д =( Q₁, Q₂)  ( Q₁₁, Q₁₂, Q₁₂, Q₂₂).

Определяем функцию переходов на множестве Q :

G (Q₁, a) = Q^д₁₁ ; G (Q₁, b) = Q^д₁₂ ;

G (Q₂, a) = Q^д₂₁ ; G (Q₂, b) = Q^д₂₂ .

Определяем функцию переходов на дополнительном множестве Q^д :

G (Q₁₁,a) = Q^д₂₁ , т.к. Q₂ = G(Q₁, a) ;

G (Q₁₁,b) = Q^д₁₂ , т.к. Q₁ = G(Q₁, b) ;

G (Q₁₂,a) = Q^д₂₁ , т.к. Q₂₁ = G(Q₁, a) ;

G (Q₁₂,b) = Q^д₁₂ , т.к. Q₁ = G(Q₁, b) ;

G (Q₂₁,a) = Q^д₁₁ , т.к. Q₁ = G(Q₂, a) ;

G (Q₂₁,b) = Q^д₂₂ , т.к. Q₂ = G(Q₁, b) ;

300

G (Q₂₂,a) = Q^д₁₁ , т.к. Q₁ = G(Q₁, a) ;

G (Q₂₂,b) = Q^д₂₂ , т.к. Q₂ = G(Q₁, b) .

Функция выходов:

а) на множестве Q - не определена,

б) на множестве Q^д :

F(Q₁₁)= F(Q₁,a)=z;

F(Q₁₂)= F(Q₁,b)=z;

F(Q₂₁)= F(Q₂,a)=x;

F(Q₂₂)= F(Q₂,b)=y.

Граф переходов построенного автомата Мура дан на Рис. 5.11.

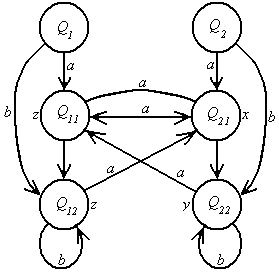
Рис. 5.11

По аналогии с автоматами Мили для автоматов Мура вводят понятия реакций и сокращенного атвомата.

Задачи.

1. Построить автомат Мура по автомату Мили, заданному в Задаче I.3 п.1.4 графом переходов (Рис.5.8).

301