2.4. Планарность графов

В некоторых случаях требуется расположить граф на двумерной поверхности (плоскость, шар, многогранник, тор и т.д.) таким образом, чтобы рёбра не пересекали друг друга.

Определение. Планарным называется граф, который может быть изображён на плоскости так, чтобы его рёбра не пересекались.

Определение. Геометрическое изображение планар-ного графа, при котором его рёбра не пересекаются, назы-вается плоским графом.

П ример 1. Рассмотрим примеры планарных графов и их плоские изображения:

Рис.4.24

Каждый планарный граф также может уложен без пе-ресечения рёбер на сфере или других видах поверхностей. Критерием планарности графов является

Теорема Понтрягина-Куратовского.

Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных графам К ₅ и К _3,3 .

Пример 2. Определить планарность графа К _4,4 .

Решение.

Поскольку граф К _4,4 содержит в качестве подграфа К _3,3 , то по теореме Понтрягина-Куратовского он не планарен.

275

Определение. Часть плоскости, ограниченная прос-тым циклом плоского графа и не содержащая внутри себя других вершин и рёбер, называется его гранью. Цикл, ограничивающих грань, называется границей грани. Грани, находящиеся внутри плоского графа, называются внутрен-ними, грань, находящаяся снаружи – внешней.

Каждое ребро плоского графа принадлежит ровно двум граням. Его удаление приводит к тому, что две грани сливаются в одну.

Для плоских графов (псевдографов) справедлива

Формула Эйлера. Если n – количество вершин, m – коли-чество рёбер, r – количество граней некоторого связного плоского графа G, то

r + n – m = 2 .

Пример 3. Проверить выполнимость формулы Эйле-ра для плоского графа G = (V,X), V = (1,2,3,4,5,6), X = ((1,2), (1,3), (1,4), (2,3), (3,4), (4,5), (4,6), (5,6)) на Рис.54.

Решение.

Характеристики графа следующие: n=6, m = 8, r=4 (3 внут-ренних грани и одна внешняя). Подставляя в формулу Эйлера, получим: 4+6-8=2.

Пример 4. Доказать, что граф К₅ не планарен.

Решение.

Основные характеристики графа следующие: n=5, m = С²₅ = (54)/(21) = 10. Если допустить планарность рассматривае-мого графа, то должно существовать его плоское изображе-ние. Из формулы Эйлера найдём число граней в плоском изображении: r = 2 – n + m = 2 – 5 + 10 = 7. Поскольку каждая грань полного графа должна содержать не менее трёх ребер, то общее число рёбер в гранях (с учётом повто-ров при подсчёте) должно быть не меньше 21. Поскольку одно ребро может входить не более чем в две грани, то об-

276

общее число рёбер должно быть не меньше 11. Однако, m = 10. Отсюда вытекает, что плоская укладка графа К₅ не существует. Следовательно, он не планарен.

Задачи.

1. Доказать с использованием формулы Эйлера непланар-ность графа К_3,3 .

2. Доказать, что граф К ₆ не планарен двумя способами – при помощи теоремы Понтрягина-Куратовского и формулы Эйлера.

3. Проверить справедливость формулы Эйлера для деревь-ев.

4. Какое минимальное число ребер необходимо удалить из плоского графа, для того, чтобы превратить его в дерево?. Ответ обосновать.

5. Можно ли построить непланарный граф с 4 вершинами?

6. Построить непланарный граф с 6 вершинами, не содер-жащий К_3,3 .

7. Проверить планарность графа К _2,4 .

8. Доказать, что деревья являются планарными графами.

9. Проверить планарность куба В³ .

10. Построить непланарный граф с шестью вершинами, не

содержащий подграф К_3,3 .

11. Доказать, что графы, содержащие менее четырех раз-личных простых циклов всегда являются планарными.

12. Проверить планарность графа

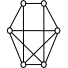
Рис.4.25

277