3. Моделирование релейных и функциональных схем.

Релейная схема, связывающая источник с k выходами и реализующая, соответственно, k функций проводимости f₁,…, f_k , описывается (k+1) - полюсной сетью c одним вход-ным и k выходными полюсами. Контакты, соответствующие переменным функций проводимости или их отрицаниям, изображаются дугами, а порядок их соединения во внут-ренних вершинах (параллельный или последовательный) определяется элементарными функциями (сложением и умножением), соединяющими переменные в функциях f₁,…, f_k. На Рис.4.16 показана 2-полюсная сеть Г = (а,b), соответ-ствующая функции проводимости f = xy x (z  u).

264

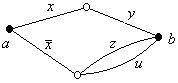
Рис.4.16

Функциональная схема, реализующая функцию n пе-ременных f₁ (х₁,…,х_n ), описывается (n+1) - полюсной сетью, в которой n полюсов – входные, а один – выходной. Элементарным функциям (, , ) поставлены в соответ-ствие вершины сети, а дуги описывают суперпозиции. На Рис.4.17 показана 4-полюсная сеть Г = (x,y,z,f), соответст-вующая функции проводимости f = (xy)(x  z):

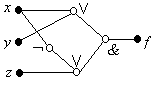
Рис.4.17

2. Операции и отображения на графах

Помимо численных характеристик на графах рассмат-ривают операции и отображения.

2.1. Изоморфизм и гомеоморфизм графов

Определение. Удалением вершины v из графа G = ( V, X) называется операция, при которой из множества V уда-ляется элемент v, а из Х - все ребра, содержащие v .

Определение. Удалением ребра х из графа G = (V, X) называется удаление элемента х из множества Х.

265

Определение. Дополнением графа G=(V,X) называет-ся графG=(V,X), гдеX -множество всех возможных ребер между V, отсутствующих в G .

Определение. Подразбиением ребра х называется опе-рация, состоящая из:

1) удаления ребра х=(v,w),

2) добавления новой вершины u и ребер (v,u), (u,w).

Пример 1. В графе G = (V, X) (V = (1, 2 , 3), X = ((1, 2), (2, 3))) из Примера 4 п 1.1 дополнение G₁ = (V₁, X₁) =(V₁ = (1, 2 , 3), Х₁ = (1, 3)) и результат подразбиения ребра (1, 2) (граф G₂ = (V₂, X₂) = (V₂ = (1, 2, 3, 4), Х₂ = ((1 ,4), (4, 2), (2, 3))) графически можно представить в следующем виде:

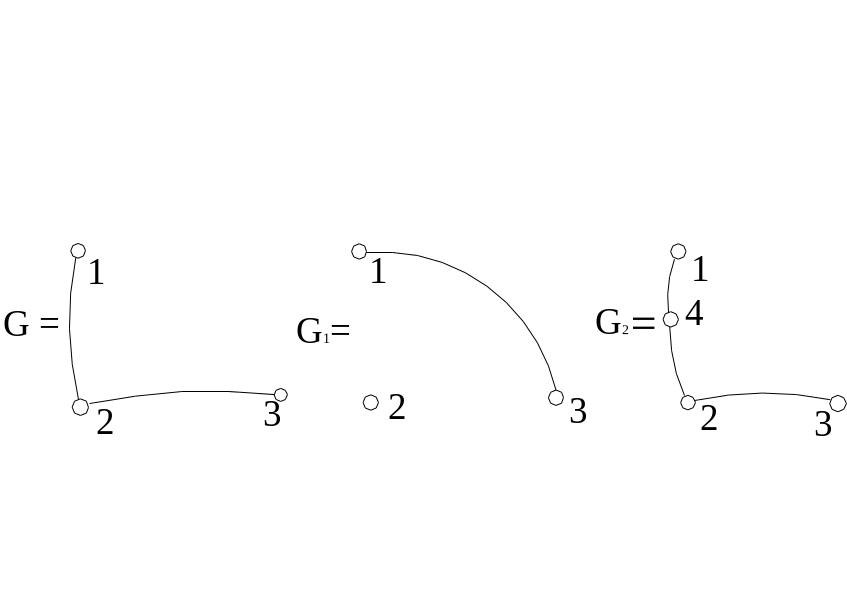
Рис.4.18

Для характеристики структурных и комбинаторных свойств графов также используется понятие изоморфизма. Данное понятие является универсальным в математике. Если заданы множества А и В с введенными на них опера-циями f₁ и f₂, то изоморфизмом называют взаимно-одно-значное отображение  множеств А в В и f₁(А) в f₂(В), сохра-няющее операции f₁ и f₂ . При этом для аА из b=(a) сле-дует: f₂(b)=(f₁(a)). В частном случае для графов определе-ние принимает следующий вид.

Определение. Графы (псевдографы) G=(V,X) и H= (W, Y) изоморфны, если существуют взаимно - однозначные отображения  : V W,  : X Y, такие, что для каждого ребра x = (v,u)  X cправедливо: (x) = ((v), (u)).

266

Можно в качестве исходных множеств у графов при-нять вершины, а операцией - соединение их ребрами, можно и наоборот – исходными считать множества ребер, а опера-цией - соединение их вершинами. Отображение  построено из двух частей -  и  .

Из взаимно – однозначного характера отображений  и  вытекают простейшие необходимые условия существо-вания изоморфного отображения графов G₁ = (V₁ , X₁ ) и G₂ = (V₂ , X₂ ) . G₁ и G₂ должны иметь одинаковые :

1) числа вершин ( V₁=V₂ );

2) числа рёбер ( Х₁=Х₂ ).

Пример 2. Рассмотрим графы G = (V, X) (V = (1, 2, 3), X = ((1, 2), (2, 3))) и Н = (W,Y) = (W = (5, 6 , 8), Y = ((5, 8),(6,8))). Они изоморфны, так как искомые взаимно-одно-значные отображения  : V W и  : X Y существуют. На Рис.4.19 они показаны графически:

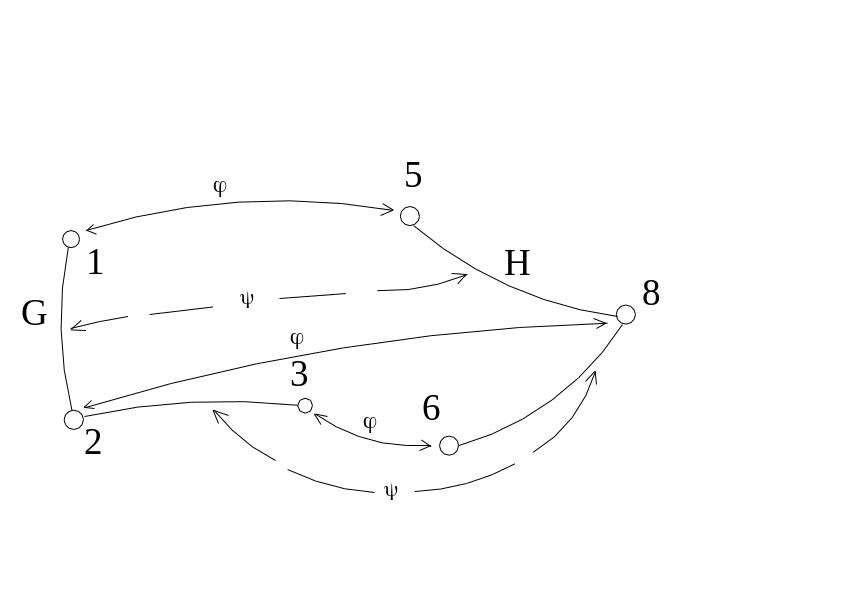
Рис.4.19

В виде списков отображения  и  можно предста-вить следующим образом:

 : {1  5; 2  8; 3  6};  : {(1,2)  (5,8); (2,3)  (6,8)}.

267

Второй возможный вариант отображений  и  име-ет вид:

 : {1  6; 2  8; 3  5};

 : {(1,2)  (6,8); (2,3)  (5,8)}.

При изоморфных отображениях соответствующие ребра соединяют соответствующие вершины. Как видно из Примера 2, задание изоморфных отображений (в том слу-чае, если они существуют) может быть выполнено неедин-ственным способом.

Определение. Автоморфизмом является изоморфное отображение графа на себя.

Пример 3. Для графа G=(V, X) из Примера 2 автомор-физм задаётся отображениями

 : {1  3; 2  2};

 : {(1,2)  (3,2); (2,3)  (2,1)}.

Определение. Граф Н является подразбиением графа G, если он может быть получен из G последовательным применением операции подразбиения рёбер.

Определение. Графы G и Н гомеоморфны, если у них существуют изоморфные подразбиения.

Задачи.

1.Выяснить изоморфизм следующих пар графов. При поло-жительном ответе построить примеры взаимно – однознач-ных отображений на множествах вершин и рёбер. Отри-цательный ответ обосновать.

а) G = (V, X), (V = (1,3 ,5,7), X = ((1,3), (3,5), (1, 7)));

Н = (W, Y),(W = (2,4 ,8), Y= ((2,8), (2,4), (4, 8)));

б) G = (V, X), (V = (1,3 ,6), X = ((1,3), (3,6), (1, 6)));

Н = (W, Y),(W = (2,4 ,7), Y= ((2,7), (4, 7)));

в) G = (V, X), (V = (1,3 ,6), X = ((1,3), (3,6), (1, 6)));

Н = (W, Y),(W = (2,5 ,7), Y= ((2,7), (2,5), (5, 7)));

г) G = (V, X), (V = (1,2 ,5,8), X = ((1,2), (2,5), (1,5)));

Н = (W, Y),(W = (3,4 ,6, 9), Y= ((3,9), (4,9), (6,9))).

268

2. Перечислить все возможные неизоморфные графы с тре-мя вершинами.

3. Перечислить все возможные неизоморфные деревья с четырьмя вершинами.