1.5. Единичные n – мерные кубы

Определение Единичным n – мерным кубом называ-ется граф, у которого вершинам соответствует полный на-бор булевых векторов длины n, а рёбра соединяют между собой все вершины, соответствующие соседним наборам (которые различаются ровно по одной координате).

Обозначается n – мерный куб Вⁿ. Количество вершин в Вⁿ равно 2ⁿ. Примеры n – мерных кубов при n = 1, 2, 3 приведены на Рис.4.14.

Рис.4.14

260

В Разделе II даны определения сферы и шара в еди-ничных n – мерных кубах, а также введено расстояние Хэм-минга на множестве булевых векторов длины n. Рассмотрим примеры применения данного вида графов.

1. Комбинаторика и алгебра логики.

Как было показано выше, сама структура кубов обес-печивает широкое их применение при изучении и интер-претации свойств булевых наборов и булевых функций, за-данных на них, поскольку многие свойства данных объек-тов проявляются именно на соседних наборах.

2. Теория кодирования.

Единичные n – мерные кубы также являются наиболее удобным объектом для изучения свойств и иллюстрации структуры двоичных кодов, которые являются наиболее распространенным видом кодов.

Задачи.

1. Найти число рёбер в кубе Вⁿ.

2. Сколькими различными способами можно сопоставить

вершинам куба Вⁿ множество всех булевых векторов длины n ?

3. Доказать, что если две вершины куба Вⁿ не соединены ребром, то расстояние Хэмминга между соответствующими булевыми векторамиⁿ, ⁿ лежит в интервале [2,n].

4. В кубе Вⁿ выделены два непересекающихся шара оди-накового радиуса. Каков может быть максимальный радиус данных шаров?

1.6. Сети

Определение. Псевдограф G = (V, X), у которого вы-делено некоторое множество из k вершин Р={v₁ ,…,v_k} , ко-торые называют полюсами , называют k–полюсной сетью. Обозначают данную сеть как Г = (Р, V, X) , Г = ({v₁ ,…,v_k }, V, X) либо Г = (v₁ ,…,v_k ).

261

Определение. Вершины сети, отличные от полюсов, называют внутренними .

Определение. Простые цепи, соединяющие полюсы сети, называют цепями сети . Цепи сети минимально воз-можной длины называют кратчайшими.

Определение. Множество ребер, удаление которых разрывает все цепи сети, называют разрезом . Разрез с ми-нимально возможным числом ребер называют минималь-ным.

На практике наибольшее применение нашли одно- и двухполюсные сети. Деревья с выделенной корневой вер-шиной (корневые) являются однополюсными сетями. Рас-смотрим основные примеры применения сетей.

1. Однополюсные сети - корневые деревья.

Выше рассмотрены примеры применения корневых деревьев в теории множеств, комбинаторике и теории ве-роятностей, булевой алгебре, теории автоматического вы-вода. Также данные сети широко используются в теории алгоритмов и других областях математики.

2. Сетевое планирование.

Любую задачу по проектированию либо построению достаточно сложного объекта (проект) можно разбить на ряд более мелких составляющих шагов. От правильного выбора последовательности выполнения данных шагов зависят сроки выполнения всего проекта.

Весь комплекс действий по выполнению проекта мо-жет быть представлен в виде совокупности событий и ра-бот. Событиями называют отдельные этапы проекта. Рабо-тами называют процесс выполнения данных этапов. Весь комплекс событий и работ, необходимых для выполнения проекта, может быть представлен в виде двухполюсной сети Г = ({v_и , v_з }, V, X), в которой:

а) все события обозначены множеством вершин V, среди них выделено исходное событие v_и (начало работ) и завер-

262

шающее событие v_з (завершение выполнения всего проек-

та), внутренние вершины сети обозначают промежуточные события – некоторые этапы, которые необходимо выпол-нить в процессе реализации проекта,

б) все работы обозначены дугами, соединяющими между

собой пары событий - вершин.

Графическое изображение данной сети называют се-тевым графиком. Для обозначения последовательности дей-ствий в сетевой график вводят также фиктивные работы, которые не связаны с выполнением каких-либо действий. Соответствуюшие работы обозначают штриховыми дугами.

В качестве примера рассмотрим организацию некото-рого производства. Проект требует выполнения следующих работ:

I) маркетинговые исследования, II) предпроектные исследо-вания по оборудованию, III) организация сети сбыта, IV) проведение рекламной кампании, V) разработка техничес-кого задания на производственное оборудование, VI) разра-ботка технической документации на производственные по-мещения и коммуникации, VII) закупка стандартного обо-рудования, VIII) проектирование и изготовление нестан-дартного оборудования, IX) строительство производствен-ных помещений и монтаж коммуникаций, X) монтаж стандартного оборудования, XI) монтаж нестандартного оборудования, XII) пусконаладочные работы,

Данные работы обозначим в сетевом графике дугами с соответствующими номерами.

Событиями в данном проекте будут следующие:

1) начало работ (исходное событие), 2) завершение марке-тинговых исследований, 3) завершение предпроектных ис-следований, 4) организация сети сбыта, 5) организация рекламной кампании, 6) подготовка технического задания на производственное оборудование, 7) завершение раз-работки технической документации на производственные

263

помещения и коммуникации, 8) завершение закупки стан-

дартного оборудования, 9) завершение проектирования и изготовления нестандартного оборудования, 10) завершение строительства производственных помещений и монтажа

коммуникаций, 11) завершение установки оборудования и пуско-наладочных работ, 12) завершение проекта (заверша-ющее событие).

Обозначим перечисленные события вершинами с со-ответствующими номерами. Сетевой график выполнения проекта дан на Рис. 4.15:

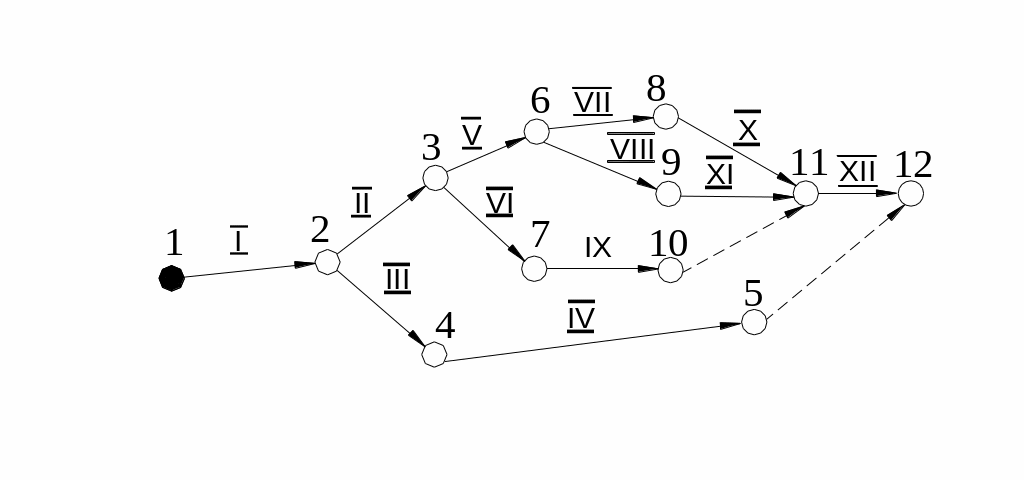
Рис.4.15