1.2. Деревья
Определение. Связный граф, не содержащий циклов, называется деревом. Дерево с n вершинами обозначается Тn.
Пример дерева (Т9) показан на Рис.4.6 а).
Определение. Граф, не содержащий циклов (состоя-щий из деревьев), называется лесом. Лес, содержащий n вершин и k деревьев, обозначается Wn,k .
Пример леса (W16,3) приведен на Рис. 4.6 б).
252
Рис.4.6
Определение. Звездой называется дерево, у которого все рёбра инцидентны в одной вершине, которая называется центром звезды. Рёбра звезды называются лучами .
Примеры звёзд с количеством лучей m = 0,1,5,8 пока-заны на Рис.4.7.
Рис.4.7
Определение. Остовным деревом графа G = (V, X) называется его подграф-дерево Т = (VТ , XТ ), содержащий все вершины графа G (VТ =V, XТ Х).
Остовные деревья могут быть выделены в графе не-единственным образом. На Рис.4.8 приведен пример графа и его различных остовных деревьев.
Деревья являются одним из наиболее распространен-ных видов графов, используемых при анализе и синтезе систем, алгоритмов и других объектов. Рассмотрим приме-ры применения деревьев.
1. Полное бинарное дерево.
Как показано ранее, данное дерево описывает мно-жество всех 2n булевых векторов длины n, его также ис-
253
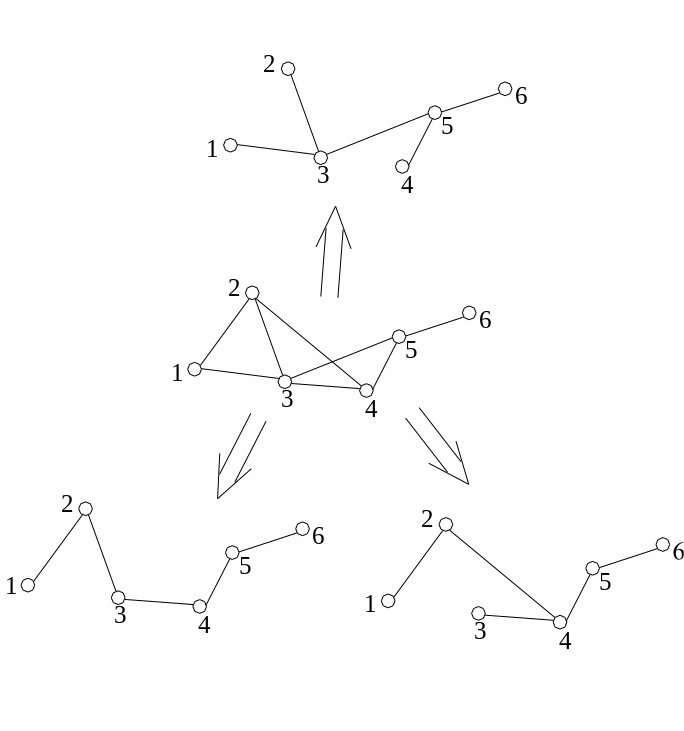
Рис. 4.8
пользуют для задания булевых функций.
2. Проблема разрешимости. Теория автоматического вывода.
2.1. Семантические деревья.
Полное семантическое дерево, являющееся частным случаем полного бинарного дерева, используется при дока-зательстве невыполнимости множества дизъюнктов по Тео-реме Эрбрана. Также в ней рассматривается закрытое се-мантическое дерево (подграф полного).
2.2. Деревья резолютивного вывода.
Резолютивный вывод невыполнимости множества дизъюнктов можно изобразить в виде дерева вывода. При-меры построения данных деревьев рассмотрены в Разделе III.
254
3. Комбинаторика. Теория вероятности.
При помощи деревьев хорошо иллюстрируются мето-ды подсчета чисел сочетаний. Допустим, необходимо найти все возможные способы размещения на трех позициях объ-ектов из наборов {a}={a1 , a2 , a3 }, {b}={b1, b2 ,b3 , b4 } и {c}={c1, c2} при условии, что на первой позиции может быть размещен один из объектов {a}, на второй – один из объ-ектов {b}, на третьей – один из {c}, размещения на позициях осуществляются независимо. Найти вероятность появления каждой комбинации при условии равновероятного их появ-ления.
Решение.
Полное множество размещений получаем при помощи дерева, растущего из начальной вершины (корня) вниз.
а) Из корня (вершины нулевого уровня) проводим ребра, соответствующие всем объектам {a1 , a2 , a3 } из набора {a}. Получаем вершины первого уровня.
Рис.
4.9
255
б) Из каждой вершины первого уровня проводим ребра, соответствующие всем объектам {b1, b2 ,b3 , b4 } . Получаем вершины второго уровня.
В) Из вершин второго уровня проводим ребра, соответству-ющие объектам {c1, c2}. Полученные вершины третьего уровня описывают все искомое множество размещений.
Дерево на Рис.4.9 показывает способ образования всех возможных комбинаций. Общее их число равно 3 4 2 = 24. Вероятность появления каждой из них равна 1/24.
4. Иерархические структуры и процессы .
Во многих структурах и алгоритмах на элементах вво-дится некоторый порядок (иерархия). Если каждый из эле-ментов низкого порядка связан только с одним элементом более высокого порядка и не имеет связей с элементами такого же порядка, то данная структура называется иерар-хической и может быть отображена в виде дерева. Данную структуру имеют многие совокупности вложенных мас-сивов, например, файловая структура памяти ЭВМ. Также иерархическую структуру имеют многие алгоритмы при-нятия решений и т.д.
Остовные деревья используются при формировании систем уравнений, описывающих функционирование элект-рических, гидравлических, механических и других систем. Представления структуры молекул в виде деревьев также позволили эффективно решить целый ряд прикладных задач в химии.
Задачи.
1. Доказать, что в любом дереве Тn число рёбер равно n-1.
2. Доказать, что любой лес Wn,k имеет число рёбер n - k.
3. Cвязный граф имеет один цикл длины m . Сколькими спо-собами можно выделить в нем остовное дерево?
4. Доказать, что в любом дереве Тn , имеющем хотя бы одно ребро, число висячих вершин не менее 2.
256