Заключение к разделу “математическая логика”
Рассмотренные в разделе логики построены на буле-вых алгебрах. Классификацию их можно построить по двум основным признакам.
1. Мощность множества значений истинности k. Все логики можно разделить на:
а) алгебру логики ( k=2 ),
б) многозначные логики ( 2 < k < 0 ),
в) счётнозначные логики (k =0 ),
г) континуальные логики (k= С ).
k=0. Счётнозначные логики могут быть получены пу-тем обобщения многозначных при k. В итоге получается логика со счетной мощностью (0) значений истинности. Обозначается такая логика Р0 . Множеством значений ис-тинности в Р0 является расширенный (включающий 0) натуральный ряд N0 = {0, 1, ... }. Элементарные функции вводятся по аналогии с Рk. Cущественной особенностью данных логик является теоретическая невозможность пол-ного задания функций табличным методом. Применяется аналитическое задание, а фрагменты таблиц используют только для иллюстрации свойств соответствующих функ-ций.
k=С. Из логик с множеством значений истинности мощ-ности континуум рассмотрена только одна – нечеткая логи-ка, у которой значения истинности k [0,1] . Другим из-вестным примером континуальной логики с таким же мно-жеством значений истинности является теория вероят-ности. Предметным для неё является множество событий, на котором введены невозможное и достоверное события, выполняющие роль нулевого и единичного элементов, а
244
также операции отрицания, сложения и умножения. Данные операции введены таким образом, что алгебра событий (множество событий с введенными на нем операциями) об-разует булеву алгебру, в которой выполняются все 13 ак-сиом булевой алгебры. Логическая функция, заданная на множестве булевой алгебры событий, называется вероят-ностью. В отличие от нечеткой логики, она задаёт степень правдоподобности, возможности наступления соответству-ющего события. Как видно из приведенного примера, функциональные свойства логики во многом определяются содержанием логической функции и набора элементарных функций, введенных на предметной области. Вариантов выбора этих функций существует бесконечное множество.
После того, как в логике указано предметное мно-жество, логическая и элементарные функции, вводятся кон-струкции, называемые формулами. В математической логи-ке вторым существенным классификационным признаком является сложность формул, допускаемых в логике.
2. Сложность формул.
Как показано в логике предикатов, при одном и том же числе истинностных значений введение кванторов и предикатов позволяет получить значительно более сложную логику, включающую в себя исходную (бескванторную) в качестве частного случая. По сложности формул логики можно разделить на:
а) элементарные - не использующие кванторов и предика-тов,
б) логики первого порядка - допускающие предикаты и кванторы по предметным переменным,
в) логики второго порядка, у которых кванторы допуска-ются и по функциональным переменным и т.д.
В виде схемы общая классификаций логик по двум вышеприведенным признакам представлена на Рис.3.27.
245
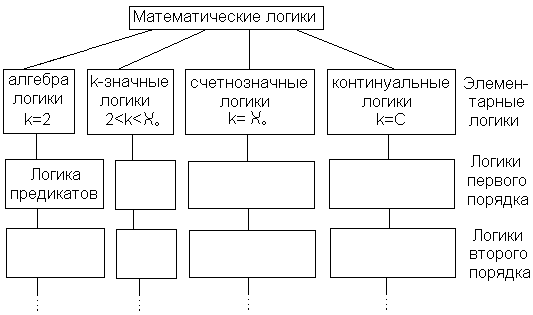
Рис.3.27
Как было показано, рассмотренные основные кон-структивные признаки только частично определяют каждую конкретную логику. Выработанные в математике приёмы позволяют строить логические теории, описывающие раз-личные явления на множествах объектов самой разной природы.
В науке основополагающая роль логики заключается в формализации знаний, в процессе которой систематизиру-ются соответствующие факты, явления и закономерности, выявляеся общность методов исследования в различных дисциплинах, границы применимости теорий и т.д.
Основное практическое значение формализации логи-ческих систем заключается в их последующей реализации при помощи различного рода вычислительных устройств, что позволяет создавать программные продукты и системы (например, робототехнические), обладающие элементами искусственного интеллекта. Применение логических мето-дов при расчете и проектировании сложных технических систем за счёт введения логических связей между объекта-ми позволяет намного упростить оперирование с ними, процессы композиции и декомпозиции.
246