Линейные операции над векторами

Сложение вектора производится по правилу параллелограмма: векторы и сносятся в общую точку (рис. 4.1), на них строят параллелограмм и его диагональ называют суммой векторов и .

Поскольку вектор равен , то можно дать другое правило нахождения суммы (правило треугольника): суммой векторов и является вектор, идущий из начала в конец , если вектор приложен к концу вектора , т.е.:

Это правило распространяется на любое число слагаемых: если векторы образуют ломаную , то суммой этих векторов является вектор , замыкающий эту ломаную, т.е.:

В частности, если ломаная замыкается, т.е. , то сумма ее звеньев равна нуль-вектору .

Сложение векторов подчиняется обычным законам сложения ‑ сочетательному и переместительному, а также обладает обратной операцией – вычитанием.

Разностью двух векторов и , отложенных от одной точки является вектор, направленный из конца вычитаемого вектора в конец уменьшаемого вектора , т.е. (Рис. 4.2.). Это правило следует из формулы (1): т.к. , то .

Векторы можно не только складывать и вычитать, но и умножать на числа (скаляры).

Вектор равен , где ‑ некоторое число, если:

1. коллинеарен ;

2. длина вектора отличается от длины вектора в 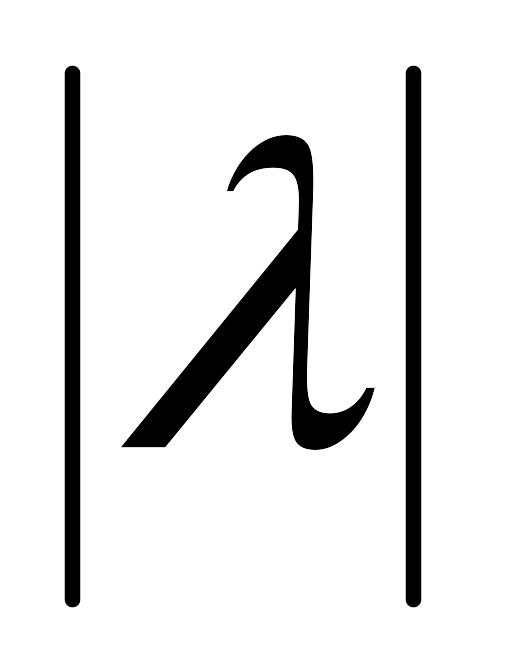раз, т.е. ;

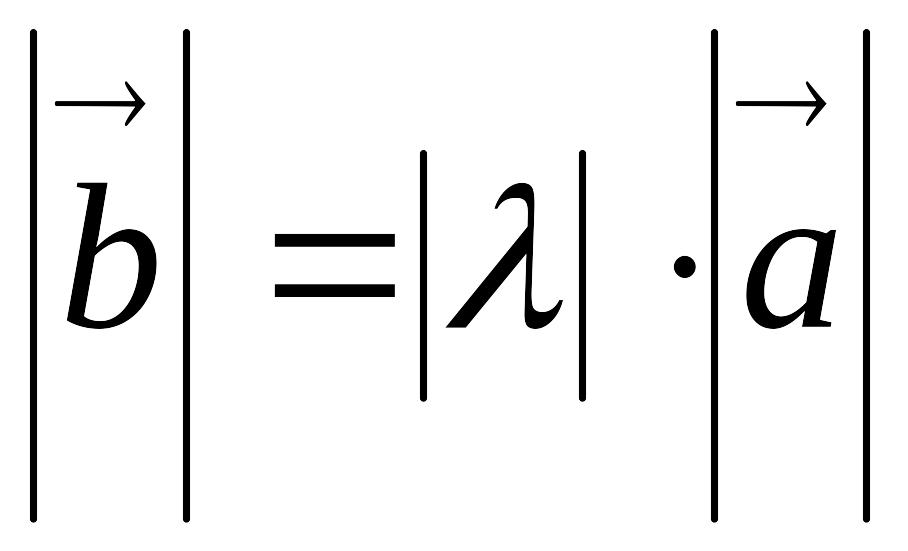3. при 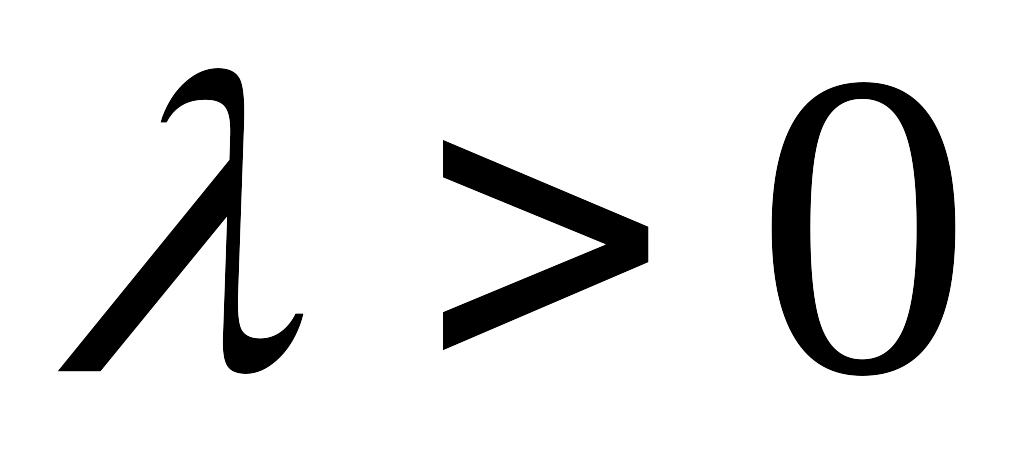, и направлены в одну сторону, при 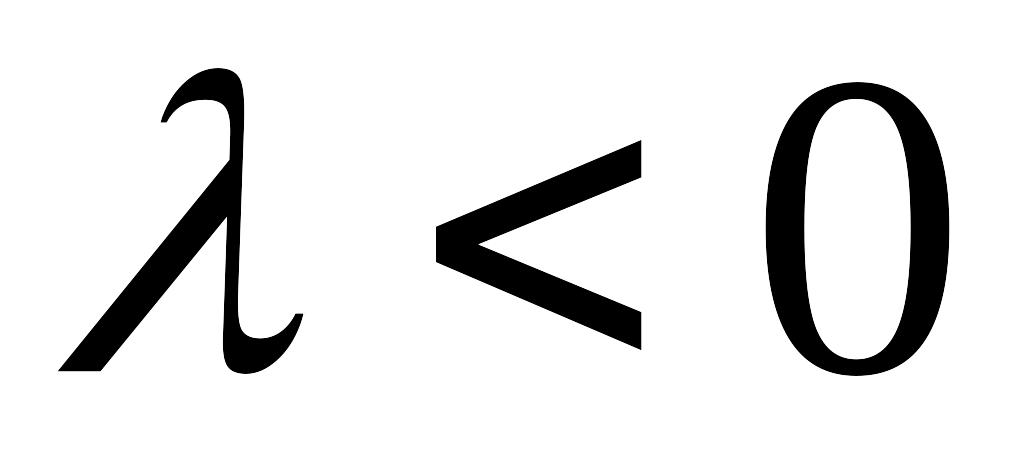‑ в разные.

Произведение вектора на скаляр обладает следующими свойствами:

1. ;

2. ;

3. ;

4. ;

5. .

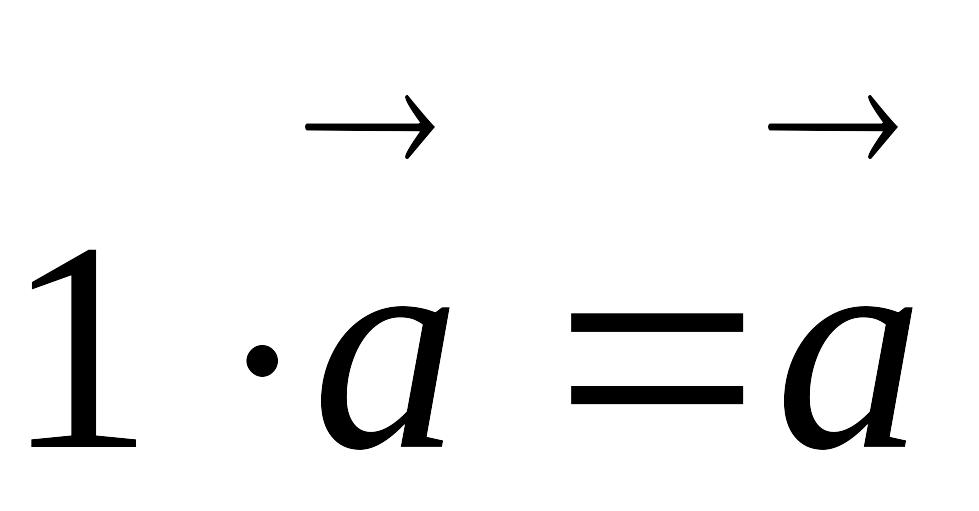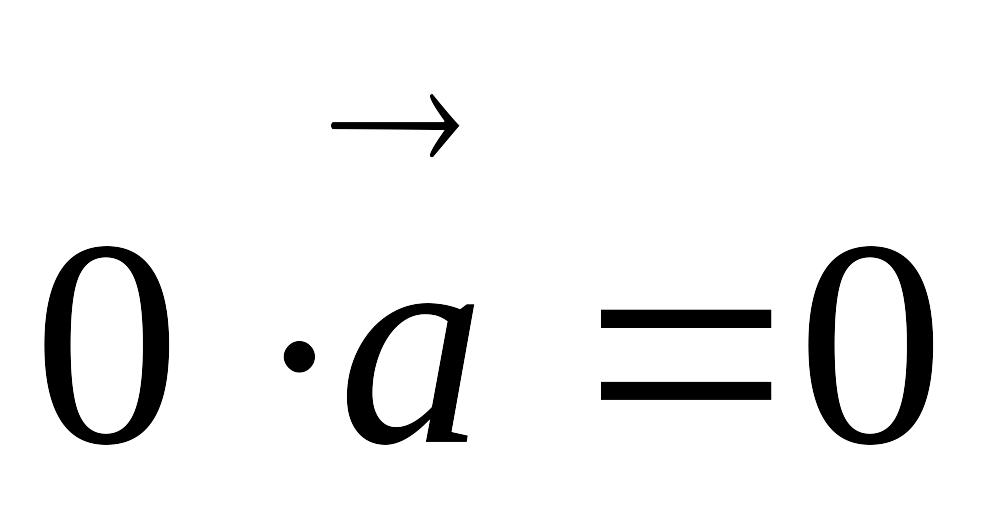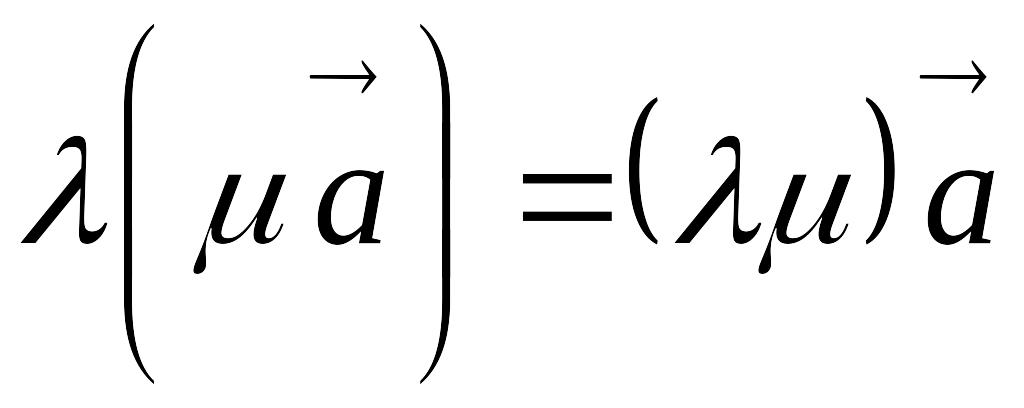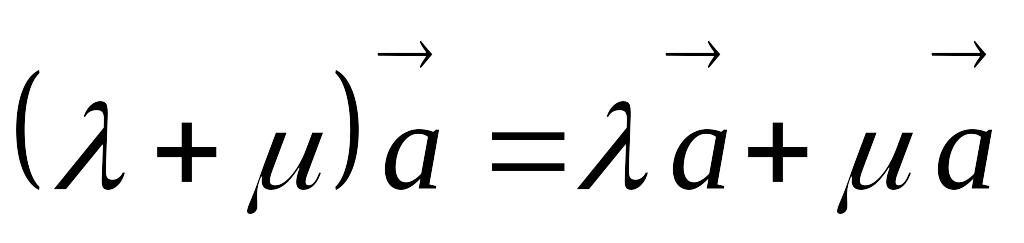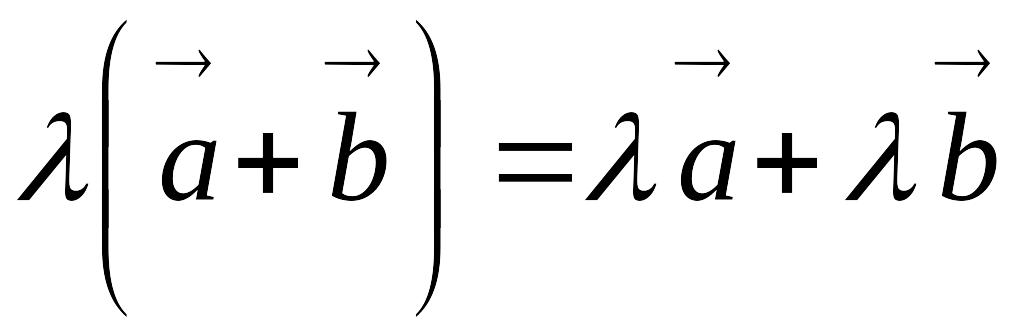Базисом на прямой называется любой ненулевой вектор на этой прямой. Любой другой вектор , коллинеарный данной прямой, может быть выражен через вектор в виде .

Базисом на плоскости называются любых два линейно независимых вектора и этой плоскости, взятые в определенном порядке. Любой третий вектор , компланарный плоскости, на которой выбран базис , может быть представлен в виде .

Базисом в трехмерном пространстве называются любые три некомпланарных вектора , взятые в определенном порядке. Такой базис обозначается . Пусть ‑ произвольный вектор трехмерного пространства, в котором выбран базис . Тогда существуют числа такие, что:

Коэффициенты называются координатами вектора в базисе , а формула (4.5) есть разложение вектора по данному базису.

Координаты вектора в заданном базисе определяются однозначно. Введение координат для векторов позволяет сводить различные соотношения между векторами к числовым соотношениям между их координатами. Координаты линейной комбинации векторов равны таким же линейным комбинациям соответствующих координат этих векторов.

19. Скалярное произведение векторов.

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Если угол между векторами  ,   обозначить через  , то их скалярное произведение можно выразить формулой

Скалярное произведение векторов  ,   можно выразить также формулой , или  .

Из формулы (1) следует, что  , если   - острый угол,  , если   - тупой угол;   в том и только в том случае, когда векторы   и   перпендикулярны (в частности,  , если   или  ).

Скалярное произведение   называется скалярным квадратом вектора и обозначается символом  . Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля: .

Если векторы   и   заданы своими координатами ,  , то их скалярное произведение может быть вычислено по формуле . Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов .

Угол   между векторами ,  , дается формулой 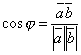 , или в координатах .

Проекция произвольного вектора   на какую-нибудь ось u определяется формулой ,где   - единичный вектор, направленный по оси u. Если даны углы  ,  ,  , которые оси u составляет с координатными осями, то   и для вычисления вектора   может служить формула .

20. Векторное произведение векторов.

Векторным произведением вектора   на вектор   называется вектор, обозначаемый символом   и определяемый следующими тремя условиями: 1). Модуль вектора   равен  , где   - угол между векторами   и  ; 2). Вектор   перпендикулярен к каждому из вектора   и  ; 3). Направление вектора   соответствует «правилу правой руки». Это означает, что если векторы  ,   и   приведены к общему началу, то вектор   должен быть направлен так, как направлен средний палец правой руки, больой палец которой направлен по первому сомножителю (то есть по вектору  ), а указательный - по второму (то есть по вектору  ).

Векторное произведение зависит от порядка сомножителей, именно: .Модуль векторного произведения   равен площади S параллелограмма, построенного на векторах   и  : . Само векторное произведение может быть выражено формулой , где   - орт векторного произведения. Векторное произведение   обращается в нуль тогда и только тогда, когда векторы   и   коллинеарны. В частности,  . Если система координатных осей правая и векторы   и   заданы в этой системе своими координатами: ,  , то векторное произведение вектора   на вектор   определяется формулой , Или .

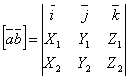21. Смешанное произведение векторов.

Тройкой векторов называются три вектора, если указано, какой из них считается первым, какой вторым и какой третьим. Тройку векторов записывают в порядке нумерации; например, запись  ,  ,   означает, что вектор   считается первым,   - вторым,   - третьим. Тройка некомпланарных векторов  ,  ,   называется правой, если составляющие ее векторы, будучи приведены к общему началу, располагаются в порядке нумерации аналогично тому, как расположены большой, указательный и средний пальцы правой руки. Если векторы  ,  ,   расположены аналогично тому, как расположены большой, указательный и средний пальцы левой руки, то тройка этих векторов называется левой. Смешанным произведенем трех векторов  ,  ,   называется число, равное векторному произведению  , умноженному скалярно на вектор  , то есть  . Имеет место тождество , ввиду чего для обозначения смешанного произведения   употребляется более простой символ  . Таким образом, ,  . Смешанное произведение   равно объему параллелепипеда, построенного на векторах  ,  ,  , взятого со знаком плюс, если тройка   правая, и со знаком минус, если эта тройка левая. Если векторы  ,  ,   компланарны (и только в этом случае), смешанное произведение   равно нулю; иначе говоря, равенство есть необходимое и достаточное условие компланарности векторов  ,  ,  . Если векторы  ,  ,   заданы своими координатами: ,  ,  , то смешанное произведение   определяется формулой 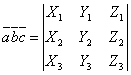. Напомним, что система координатных осей предполагется правой (вместе с тем является правой и тройка векторов  ,  , 

22. Прямая на плоскости. Различные виды уравнений прямой. Взаимное расположение двух прямых. Отклонение точки от прямой.

Прямая в пространстве может быть однозначно определена, если известна точка, принадлежащая прямой, и ненулевой вектор, параллельный прямой (направляющий вектор прямой).

Если ‑ произвольная текущая точка прямой , то вектор коллинеарен вектору и их соответствующие координаты пропорциональны.

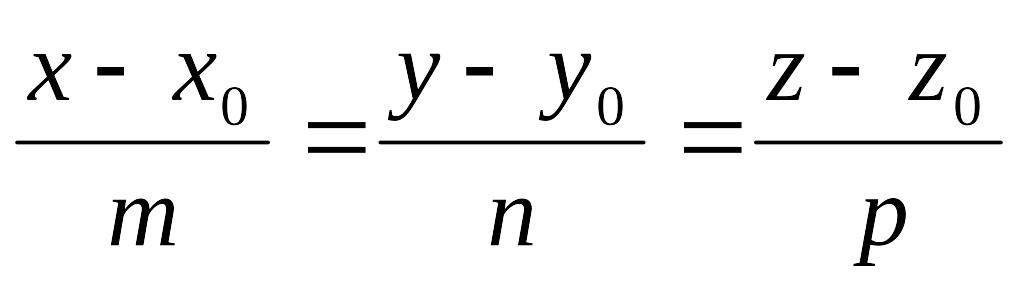
Этим соотношениям удовлетворяют координаты любой точки прямой и только этой прямой. Равенства (5.1) называются каноническими уравнениями прямой в пространстве.

Обозначим радиус-вектор точки , ‑ радиус-вектор точки . Тогда:

В силу коллинеарности векторов и существует число такое, что . Тогда из получим векторное параметрическое уравнение прямой:

В координатной форме уравнение равносильно трем уравнениям:

которые называются параметрическими уравнениями прямой в пространстве.

Система двух уравнений первой степени определяет прямую линию при условии, что нормальные векторы и неколлинеарны. Только в этом случае плоскости будут пересекаться. Уравнения (5.6) носят название «общее уравнение прямой в пространстве».

условие перпендикулярности прямых можно записать в виде: или .

Условие параллельности: .

Прямые совпадают: , т.е. .

Прямые параллельны: непараллелен , но , т.е. .

Прямые пересекаются: непараллелен , но , , ‑ компланарны, т.е.

Прямые скрещиваются: , , ‑ некомпланарны, т.е. .

23. Плоскость. Различные виды уравнений плоскости. Взаимное расположение двух плоскостей, прямой и плоскости. Отклонение точки от плоскости.

Всякая поверхность в пространстве задается в декартовых координатах уравнением вида .

Если ‑ многочлен -й степени, то соответствующая поверхность называется алгебраической поверхностью -го порядка или просто поверхностью -го порядка.

Всякая поверхность 1-го порядка есть плоскость, т.е. всякое уравнение 1-й степени:

определяет плоскость. Уравнение (6.1) называется общим уравнением плоскости.

Вектор , координатами которого являются коэффициенты при в уравнении (6.1), перпендикулярен плоскости (6.1) по свойству скалярного произведения векторов. Этот факт будет постоянно использоваться в дальнейшем. Вектор называют нормальным вектором плоскости

Уравнение плоскости, проходящей через данную точку перпендикулярно вектору , имеет вид:

Очевидно, что уравнение (6.1) имеет смысл только тогда, когда хотя бы один из коэффициентов не равен нулю.

уравнению плоскости в отрезках:

Нормальным уравнением плоскости называется уравнение:

где ‑ углы между перпендикуляром, опущенным из начала координат на плоскость, и положительным направлением осей координат, а ‑ расстояние от плоскости до начала координат.

Отклонением точки от плоскости называется ее расстояние от плоскости, взятое со знаком плюс, если точка и начало координат лежат по разные стороны от плоскости (Рис. 6.1), и со знаком минус – если и лежат по одну сторону от плоскости.

Отклонение точки от плоскости определяется по формуле .

Прямая в пространстве. Различные виды уравнений прямой в пространстве. Прямая в пространстве может быть однозначно определена, если известна точка, принадлежащая прямой, и ненулевой вектор, параллельный прямой (направляющий вектор прямой).

Если ‑ произвольная текущая точка прямой , то вектор коллинеарен вектору и их соответствующие координаты пропорциональны.

Этим соотношениям удовлетворяют координаты любой точки прямой и только этой прямой. Равенства (5.1) называются каноническими уравнениями прямой в пространстве.

Обозначим радиус-вектор точки , ‑ радиус-вектор точки . Тогда:

В силу коллинеарности векторов и существует число такое, что . Тогда из получим векторное параметрическое уравнение прямой:

В координатной форме уравнение равносильно трем уравнениям:

которые называются параметрическими уравнениями прямой в пространстве.

Система двух уравнений первой степени определяет прямую линию при условии, что нормальные векторы и неколлинеарны. Только в этом случае плоскости будут пересекаться. Уравнения (5.6) носят название «общее уравнение прямой в пространстве».

условие перпендикулярности прямых можно записать в виде: или .

Условие параллельности: .

Прямые совпадают: , т.е. .

Прямые параллельны: непараллелен , но , т.е. .

Прямые пересекаются: непараллелен , но , , ‑ компланарны, т.е.

Прямые скрещиваются: , , ‑ некомпланарны, т.е. .

25. Кривые второго порядка. Окружность.

Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое еёрадиусом.

Радиус — не только величина расстояния, но и отрезок, соединяющий центр окружности с одной из её точек.

Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называетсядиаметром.

Окружность называется единичной, если ее радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.

Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Угол, образуемый дугой окружности, равной по длине радиусу, принимается за 1 радиан.

Длина единичной полуокружности обозначается через π.

Геометрическое место точек плоскости, расстояние от которых до данной точки не больше, чем заданное ненулевое, называется кругом.

Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Прямая, проходящая через две различных точки окружности, называется секущей.

Центральный угол — угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую опирается.

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.

Две окружности, имеющие общий центр, называются концентрическими.

Две окружности, пересекающиеся под прямым углом, называются ортогональными.

Изопериметрическое неравенство: Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.

Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).

Касательная к окружности всегда перпендикулярна её диаметру, один из концов которого является точкой касания.

Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.

Точка касания двух окружностей лежит на прямой, проходящей через их центры.

Длину дуги окружности радиуса R, образованной центральным углом  , измеренным в радианах, можно вычислить по формуле L= φR.

Длину окружности с радиусом R можно вычислить по формуле  .

Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°.

Два вписанных угла, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на дугу длиной в половину окружности равен 90°.

Угол между двумя секущими, проведёнными из точки, лежащей вне окружности равен полуразности мер дуг, лежащих между секущими.

Угол между пересекающимися хордами равен полусумме мер дуги, лежащей в угле и дуги напротив нее.

Угол между касательной и хордой равен половине градусной меры дуги, стягиваемой хордой.

Отрезки касательных к окружности, проведённых из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

При пересечении двух хорд произведение отрезков, на которые делится одна из них точкой пересечения, равно произведению отрезков другой.

Произведение длин расстояний от выбранной точки до двух точек пересечения окружности и секущей, проходящей через выбранную точку, не зависит от выбора секущей и равно абсолютной величине степени точки относительно окружности.

Квадрат длины отрезка касательной равен произведению длин отрезков секущей и равен абсолютной величине степени точки относительно окружности.

Окружность является простой плоской кривой второго порядка.

Окружность является коническим сечением и частным случаем эллипса.

26. Кривые второго порядка. Эллипс.

Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек и есть величина постоянная (большая, чем расстояние между и ).

Точки и называются фокусами эллипса. Обозначив расстояние между фокусами через , а сумму расстояний от точек эллипса до фокусов через , имеем . Если это условие не выполнено, то рассматриваемое множество точек либо отрезок прямой, заключенной между фокусами, либо не содержит ни одной точки.

Из определения эллипса вытекает следующий метод его построения: если концы нерастяжимой нити длины закрепить в точках и и натянуть нить острием карандаша, то при движении острия будет вычерчиваться эллипс с фокусами и и с суммой расстояний от произвольной точки эллипса до фокусов, равной

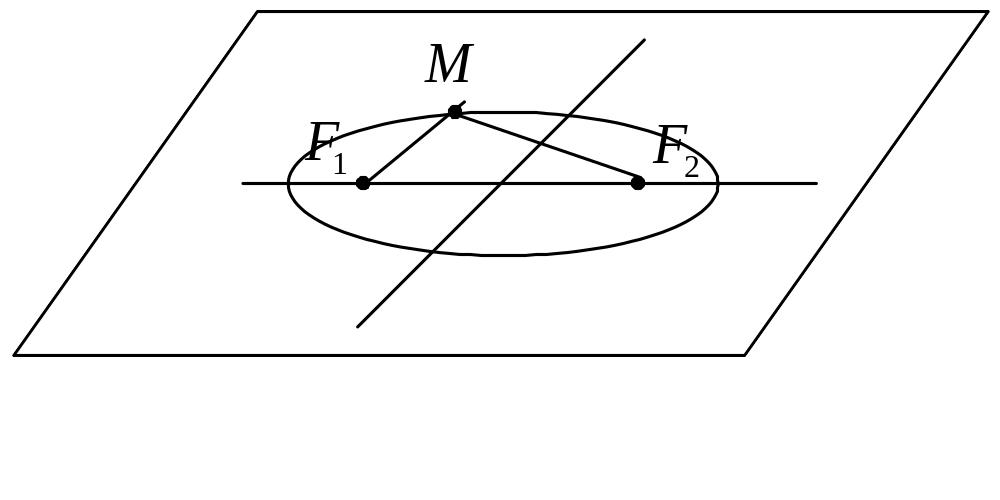
Составим уравнение эллипса. Для этой цели расположим декартову прямоугольную систему координат таким образом, чтобы ось походила через фокусы и , положительное направление оси – от к , начало координат выберем в середине отрезка . Тогда координаты точек и будут соответственно и .

Пусть ‑ произвольная точка эллипса, тогда: , .

По определению эллипса . Подставляя сюда значения и , имеем:

Уравнение (1) и есть уравнение эллипса. Преобразуя, упростим его:

Возведя обе части уравнения в квадрат и приведя подобные члены, получим: .

Возведем еще раз обе части в квадрат и приведем подобные члены. Получаем или

Положительную величину обозначим через . Тогда уравнение (7.2) примет вид:

Оно называется каноническим уравнение эллипса.

Координаты точек эллипса ограничены неравенствами . Значит, эллипс ограниченная фигура, не выходящая за пределы прямоугольника со сторонами и _:

Заметим, что в уравнение (7.3) входят лишь четные степени и . Поэтому, если точка принадлежит эллипсу, то и точки , , также ему принадлежат. А это означает, что эллипс – линия симметричная относительно координатных осей и Поэтому для исследования формы эллипса достаточно рассмотреть его в первой координатной четверти, а в остальных четвертях его строение определяется по симметрии. Для первой четверти, из уравнения имеем:

При возрастании от до , монотонно убывает от до .

Оси симметрии эллипса (оси и ) называются просто его осями, а центр симметрии – точка ‑ центром эллипса. Точки пересечения эллипса с осями координат называются вершинами эллипса. Отрезки и , а также их длины и называются полуосями эллипса. В случае, когда фокусы эллипса находятся на оси (как в нашем случае), из равенства , следует, что . В этом случае называется большой полуосью, а ‑ малой.

Если , то уравнение (7.3) можно переписать в виде:

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси . Пусть на плоскости выбрана прямоугольная система координат . Тогда преобразование, переводящее произвольную точку в точку , координаты которой задаются формулами , будет окружность (4) переводить в эллипс, заданный соотношением .

Ч

исло называется эксцентриситетом эллипса. Эксцентриситет характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении становится более вытянутым

Фокальными радиусами точки эллипса называются отрезки прямых, соединяющие эту точку с фокусами и . Их длины и задаются формулами и . Прямые называются директрисами эллипса. Директриса называется левой, а ‑ правой. Так как для эллипса , то и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.

Директрисы обладают следующим свойством: отношение расстояния любой точки эллипса от фокуса к ее расстоянию до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е. .

27. Кривые второго порядка. Гипербола.

Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек и есть величина постоянная (не равная нулю и меньшая, чем расстояние между и ).

Точки и называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно . Модуль расстояний от точек гиперболы до фокусов и обозначим через . По условию, .

Выбрав декартову систему координат, как в случае эллипса, и используя определение гиперболы, составляем ее уравнение:

где ‑ координаты произвольной точки гиперболы, .

Уравнение (7.6) называется каноническим уравнением гиперболы.

Из уравнения (7.6) видно, что . Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми и .

Так как в уравнение входят только четные степени и , то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем: .

График этой функции от точки уходит неограниченно вправо и вверх и как угодно близко подходит к прямой:

Поэтому говорят, что гипербола асимптоматически приближается к прямой и эту прямую называют асимптотой гиперболы. Из симметрии гиперболы следует, что у нее две асимптоты .

Построим гиперболу. Сначала строим, так называемый, основной прямоугольник гиперболы, центр которой совпадает с началом координат, а стороны равны и параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы

Г ипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки и пересечения гиперболы с осью называются вершинами гиперболы. Величины и называются полуосями гиперболы. Если , то гипербола называется равносторонней.

Эксцентриситетом гиперболы называется число . Для любой гиперболы . Эксцентриситет характеризует форму гиперболы: чем меньше, тем больше вытягивается гипербола вдоль оси . На рисунке 7.9 изображены гиперболы с различными значениями .

Фокальными радиусами точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами и . Их длины и задаются формулами:

Для правой - ветви ,

Для левой - ветви .

Прямые называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением .

28. Кривые второго порядка. Парабола.

Параболой называется линия, состоящая из всех точек плоскости, равноудаленных от данной точки (фокуса) и данной прямой (директрисы).

Для вывода канонического уравнения параболы ось проводят через фокус перпендикулярно директрисе в направлении от директрисы к фокусу; начало координат берут в середине отрезка между фокусом и точкой пересечения оси с директрисой . Если обозначить через расстояние фокуса от директрисы, то 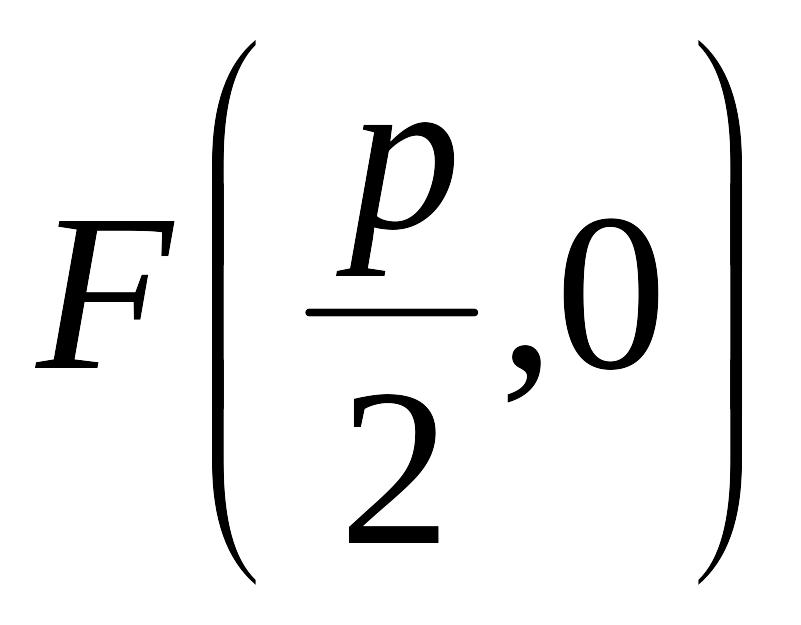и уравнение директрисы будет иметь вид .

В выбранной системе координат уравнение параболы имеет вид:

Это уравнение называется каноническим уравнением параболы. Из уравнения видно, что может принимать только неотрицательные значения. Значит, на рисунке вся парабола располагается справа от оси . Так как уравнение (7.8) содержит только в четной степени, то парабола симметрична относительно оси _, и поэтому достаточно рассмотреть ее форму в первой четверти. В этой четверти .

При неограниченном возрастании неограниченно растет и . Парабола, выходя из начала координат, уходит неограниченно вправо и вверх, четвертой четверти парабола строится по симметрии.

Ось симметрии параболы называется ее осью. Точка пересечения с ее осью называется вершиной параболы.