1. Множества, операции над множествами.

Множество – одно из важнейших понятий математики. Вводится аксиоматически и не может быть определено через какие-либо элементарные понятия.

Кантор описывает множество следующим образом:

Множество есть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества _.

Если множество состоит из конечного числа элементов, оно называется конечным. При этом число элементов множества может быть очень велико или вообще неизвестно. Множество может состоять также из бесконечного количества элементов, тогда оно называется бесконечным.

Основные операции над множествами

Суммой или объединением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из заданных множеств. Эта операция над множествами обозначается знаком .

Произведением или пересечением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих каждому из заданных множеств. Эта операция над множествами обозначается знаком . Если , то множества и называются непересекающимися.

Два множества называются непересекающимися (или расчлененными) если . Практический интерес представляют разбиения множества на взаимно непересекающиеся подмножества (эту задачу иногда называются классификацией). Разбиением множества называется такая расчлененная система непустых подмножеств множества , что каждый элемент множества является элементом некоторого единственного множества этой системы. Возможность разбиения множества на непересекающиеся подмножества зависит от признака, по которому производится разбиение.

Разностью множеств и или дополнением до называется множество, состоящее только из тех элементов , которые не входят в . Эта операция над множествами обозначается знаком .

Часто все рассматриваемые множества считают подмножествами одного основного множества . В таком случае разность (дополнение до ) обозначают, как , а операцию называют взятием дополнения.

2. Числа. Числовые множества. Счетные и несчетные множества.

Будем рассматривать множества, элементами которых являются числа. Такие множества называются числовыми. Числовые множества задаются на оси действительных чисел R. На этой оси выбирают масштаб и указывают начало отсчета и направление. Наиболее распространенные числовые множества:

‑ множество натуральных чисел;

‑ множество целых чисел;

– множество рациональных или дробных чисел;

‑ множество действительных чисел.

Множество всех рациональных чисел является счетным множеством. Счетным является множество всех точек плоскости (пространства) имеющих рациональные координаты.

Множество всех действительных чисел является несчетным: оно имеет мощность, называемую континуумом.

3. Границы и грани числовых множеств.

Некоторое непустое подмножество множества действительных чисел называют ограниченным сверху (снизу), если существует действительное число такое, что выполняется неравенство ( ).

Всякое число с указанным свойством называют верхней (нижней) гранью множества .

Непустое подмножество множества действительных чисел называется ограниченным, если оно ограничено и сверху и снизу.

В противоположность этому определению, множество называется неограниченным сверху (снизу), если какое бы число мы бы не предложили в качестве верхней (нижней) границы множества , всегда найдется элемент этого множества, который будет больше (меньше) .

Множество, неограниченное как сверху, так и снизу, называется неограниченным множеством.

Элементы комбинаторики. Формула Ньютона.

Раздел элементарной математики, в котором для конечных множеств рассматриваются различные соединения элементов, такие, как сочетания, размещения, перестановки, а также все виды соединений с повторениями называется комбинаторика. Задачи комбинаторики впервые рассматривались в связи с возникновением теории вероятностей, где к задачам комбинаторики приводит подсчет вероятностей на основе гипотезы равновозможных элементарных событий.

Размещениями из элементов по ( ) называют их соединения, каждое из которых содержит ровно различных элементов (выбранных из данных элементов) и которые отличаются либо сами элементами, либо порядком элементов.

Соединения из элементов, каждое из которых содержит все элементов, и которые отличаются лишь порядком элементов, называются перестановками .

Сочетаниями из элементов по ( ) называют такие их соединения, каждое из которых содержит ровно данных элементов, и которые отличаются хотя бы одним элементом.

Числа являются коэффициентами в формуле бинома Ньютона:

Свойства сочетаний:

1. 

2. 

3. 

4. 

5. 

Отображения, виды отображений, композиция отображений, Обратное отображение.

Отображение – одно из основных понятий математики. Отображение есть какое-либо правило или закон соответствия множеств. Пусть и – произвольные непустые множества. Говорят, что задано отображение множества на множество (запись: или ) если каждому элементу множества (  поставлен соответствие единственный, однозначно определенный элемент множества ( .

Отображение называется сюръективным, когда каждый элемент множества (  имеет хотя бы один прообраз множества ( , т.е. , или .

Отображение называется инъективным, когда каждый элемент множества (  является образом лишь одного элемента множества ( , т.е. образы любых двух различных элементов множества различны, т.е. из следует .

Отображение называется биективным или взаимно однозначным, когда оно одновременно инъективно и сюръективно, т.е. каждый элемент множества является образом одного и только одного элемента множества .

Равенство двух отображений и означает по определению, что их соответствующие области совпадают ( и ), причем .

Произведение двух отображений и можно определить как отображение , которое каждому элементу множества ставит в соответствие элемент множества .

Отображение множества на множество иначе называется функцией на множестве со значениями во множестве . Если множества и совпадают, то биективное отображение множества на себя называется преобразованием множества . Простейшее преобразование множества – тождественное – определяется так: . Тождественное отображение , переводящее каждый элемент в себя, также называют единичным преобразованием. Если заданы преобразования и , то преобразование , являющееся результатом последовательного выполнения сначала преобразования , а затем и преобразования , называется произведением преобразований и : .

4. Комплексные числа.

в множестве действительных чисел такое простое уравнение не имеет решений. Так как многие задачи практики приводят к алгебраическим уравнениям, требуется построить новое множество, содержащее множество действительных чисел и решение любого алгебраического уравнения. Символом , который называется мнимой единицей, обозначим корень уравнения , или . Множество , которое представляет собой множество всех двучленов вида , называется множеством комплексных чисел. Действительное число называется действительной частью комплексного числа , ‑ мнимой частью или коэффициентом при мнимой единице. Два комплексных числа и будут равны тогда и только тогда, когда . При этом действительные числа рассматриваются как частный случай комплексных чисел, мнимая часть которых равна нулю ( ). Комплексное число равно нулю тогда и только тогда, когда равны нулю его действительная и мнимая части.

5. Арифметические операции над комплексными числами, комплексная плоскость, геометрическое представление, тригонометрическая форма комплексных чисел.

Алгебраическую операцию сложения на множестве можно задать следующим образом: .Сумма чисел , поэтому число является противоположным числу , тем самым определена операция вычитания .Учитывая, что через обозначен корень уравнения , т.е. или , можно определить умножение комплексных чисел:

.Чтобы определить деление комплексных чисел, нужно определить число обратное числу . Для действительного числа обратным будет число .Выражение запишем в стандартной форме. Для этого умножим числитель и знаменатель на комплексное число : ,где .

Каждому комплексному числу поставим в соответствие точку плоскости, координатами которой в прямоугольной системе координат являются числа и .

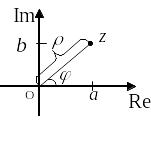При этом точки горизонтальной координатной оси изображают действительные числа и поэтому эту ось называют действительной осью, а по вертикальной оси откладываются мнимые части комплексных чисел, поэтому вертикальная ось называется мнимой осью.

Пусть . . Аргумент числа определяется из равенств , .Отсюда: -тригонометрическая форма комплексного числа.Если воспользоваться формулой Эйлера,

6. Извлечение корней из комплексных чисел и возведение в степень.

Используя формулу умножения комплексных чисел (3.3), получим формулу возведения комплексного числа в степень, называемую формулой Муавра:

Из нее следует, что для возведения комплексного числа в любую натуральную степень его модуль нужно возвести в эту степень, а аргумент умножить на показатель этой степени.

Пусть . Комплексное число называется корнем -й степени из , если , т.е.:

или .

Модуль комплексного числа определяется однозначно, поэтому или (здесь имеется в виду арифметический корень).

Аргумент комплексного числа определяется с точностью до . Следовательно, , а .

Таким образом, комплексное число , которое является корнем -й степени из имеет вид:

7. Многочлен от одной переменной. Действия с многочленами. Теорема о делении многочленов с остатком.

Многочленом от переменной степени называется выражение вида:

,где ‑ действительные или комплексные числа, называемые коэффициентами, ‑ натуральное число, ‑ переменная величина, принимающая произвольные числовые значения.

Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.

Суммой многочленов и , называется многочлен , где

Произведением многочленов и называется многочлен: где .

Многочлен называется делителем многочлена , если существует многочлен такой, что .