
Теорема о делении с остатком
Для
любых многочленов
![]() существуют многочлены
существуют многочлены
![]() и
и
![]() ,
такие, что
,
такие, что
![]() причем степень
меньше степени
причем степень
меньше степени
![]() или
или
![]() .
Многочлены
и
определены однозначно.
.
Многочлены
и
определены однозначно.
Многочлены
и
называются соответственно частным и
остатком. Если
делит
![]() то остаток
то остаток
![]() .
.
Число
![]() называется
корнем многочлена
называется
корнем многочлена
![]() ,
если
,
если
![]() .
.
Корни многочлена. Основная теорема алгебры. Разложение многочлена на неприводимые множители.
Теорема Безу
Число
является корнем многочлена
![]() тогда и только тогда, когда
делится на
тогда и только тогда, когда
делится на
![]()
Обратно,
пусть
![]() делит
,
т.е.
делит
,
т.е.
![]() .
Тогда
.
Тогда
![]() .
.
Следствие.
Остаток
от деления многочлена
на
равен
![]() .
.
Число
называется
корнем кратности
![]() многочлена
,
если
многочлена
,
если
![]() делит
,
но
делит
,
но
![]() уже не делит
.
уже не делит
.
Число различных корней многочлена не превосходит его степени.
Большое значение имеет следующая основная теорема.
Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).
Следствие.
Всякий многочлен степени
![]() имеет в C
(множестве комплексный чисел) столько
корней, какова его степень, считая каждый
корень столько раз, какова его кратность.
имеет в C
(множестве комплексный чисел) столько
корней, какова его степень, считая каждый
корень столько раз, какова его кратность.
Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.
Пусть
![]() и
и
![]() корни
корни
![]() Тогда
Тогда
![]() делится на
делится на
![]() и
и
![]() но так как у
и
нет общих делителей, то
делится на прозведение
но так как у
и
нет общих делителей, то
делится на прозведение
![]() .
.
Утверждение
2.
Многочлен
с действительными коэффициентами
степени
![]() всегда разлагается на множестве
действительных чисел в произведение
линейных многочленов, отвечающих его
вещественным корням, и многочленов 2-ой
степени, отвечающих паре сопряженных
комплексных корней.
всегда разлагается на множестве
действительных чисел в произведение
линейных многочленов, отвечающих его
вещественным корням, и многочленов 2-ой
степени, отвечающих паре сопряженных
комплексных корней.
При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.
Рациональные функции. Представление рациональной функции в виде суммы простейших.
Рациональной
дробью
называется дробь
![]() где
и
где
и
![]() ‑ многочлены с действительными
коэффициентами, причем многочлен
‑ многочлены с действительными
коэффициентами, причем многочлен
![]() .
Рациональная дробь
называется правильной, если степень
числителя меньше степени знаменателя.
Если рациональная дробь не является
правильной, то, произведя деление
числителя на знаменатель по правилу
деления многочленов, ее можно представить
в виде
.
Рациональная дробь
называется правильной, если степень
числителя меньше степени знаменателя.
Если рациональная дробь не является
правильной, то, произведя деление
числителя на знаменатель по правилу
деления многочленов, ее можно представить
в виде
![]() ,
где
,
где
![]() и
и
![]() –
некоторые многочлены, а
–
некоторые многочлены, а
![]() –
правильная рациональная дробь.
–
правильная рациональная дробь.
Лемма
1.
Если
–
правильная рациональная дробь, а число
![]() является вещественным корнем кратности
является вещественным корнем кратности
![]() многочлена
многочлена
![]() ,
т.е.
,
т.е.
![]() и
и
![]() ,
то существует вещественное число
,
то существует вещественное число
![]() и многочлен
и многочлен
![]() с вещественными коэффициентами, такие,
что
с вещественными коэффициентами, такие,
что
![]() где дробь
где дробь
![]() также является правильной.
также является правильной.
Лемма
2.
Если
–
правильная рациональная дробь, а число
![]() (
и
(
и
![]() –
вещественные,
–
вещественные,
![]() )
является корнем кратности
)
является корнем кратности
![]() многочлена
,
т.е.
многочлена
,
т.е.
![]() и
и
![]() ,
и если
,
и если
![]() ,
то существуют вещественные числа
,
то существуют вещественные числа
![]() и
и
![]() и
многочлен
с вещественными коэффициентами, такие,
что
и
многочлен
с вещественными коэффициентами, такие,
что
![]() где дробь
где дробь
![]() также является правильной.
также является правильной.
Представление в виде простейших дробей:
Раскладываем знаменатель на простые сомножители
Формально записываем равенство дроби и суммы слагаемых (кол-во слагаемых = сумме степеней сомножителя знаменателя)
Приводим к общему знаменателю эти слагаемые
Для нахождения коэффициентов – 2 метода:
-«Частных значений»: 2 многочлена равны тогда и только тогда, когда они равны при любых иксах, вход. В эти многочлены.
-«Неопределенных коэффициентов»: 2 многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях.
Матрицы. Операции над матрицами. Ранг матрицы.
Прямоугольная таблица:
состоящая
из
![]() строк и
столбцов, называется матрицей
размера
строк и
столбцов, называется матрицей
размера
![]() или
или
![]() -матрицей.
-матрицей.
Если
![]() ,
то матрица
,
то матрица
называется квадратной матрицей порядка .
В
квадратной матрице
-го
порядка диагональ, состоящая из элементов
![]() называется главной диагональю, состоящая
из элементов
называется главной диагональю, состоящая
из элементов
![]() ‑ побочной диагональю.
‑ побочной диагональю.
Квадратная матрица
называется
диагональной.
Если в диагональной матрице все
диагональные элементы равны, т.е.
![]() ,
то такая матрица называется скалярной.
Скалярная матрица, у которой
,
то такая матрица называется скалярной.
Скалярная матрица, у которой
![]() называется единичной и обозначается
буквой
называется единичной и обозначается
буквой
![]() .
.
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается через 0.
Матрицы и называются равными, если их размеры одинаковы и элементы этих матриц, стоящие на одинаковых местах, равны.
Сложение матриц обладает следующими свойствами:
Коммутативность, т.е.
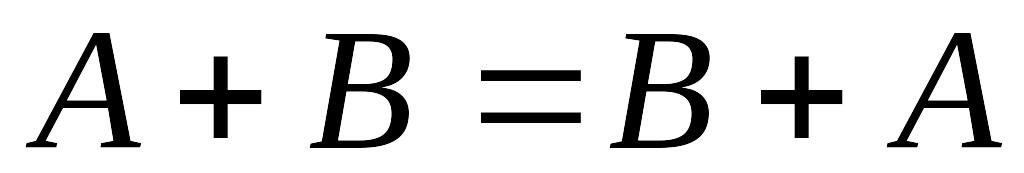 .
.Ассоциативность, т.е.
 .
.Для любых двух матриц и одинакового размера существует единственная матрица
 такая, что
такая, что
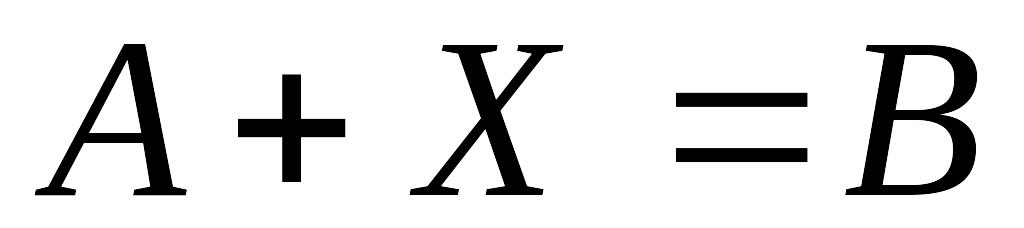 .
Матрица
обозначается
.
Матрица
обозначается
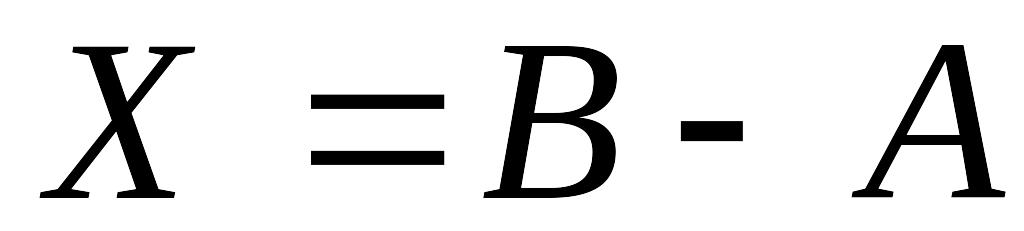 и называется разностью матриц
и
.
Уравнение
и называется разностью матриц
и
.
Уравнение
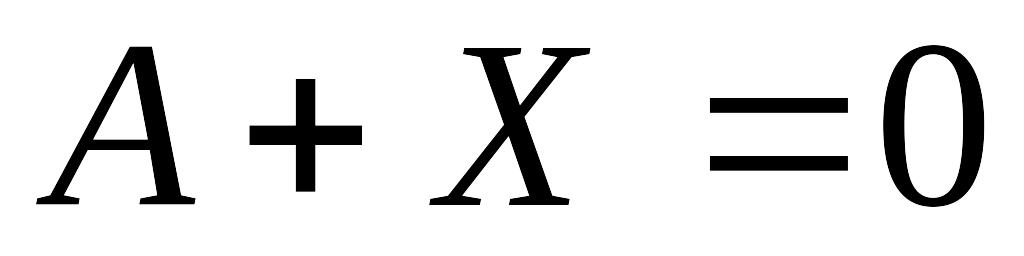 имеет решение
имеет решение
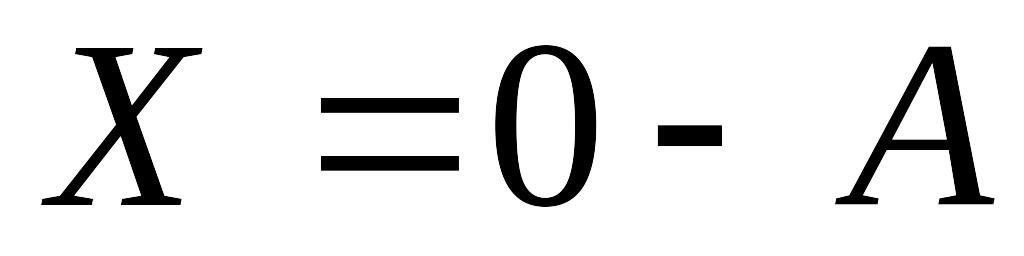 ,
получающаяся при этом матрица называется
противоположной
и обозначается
,
получающаяся при этом матрица называется
противоположной
и обозначается
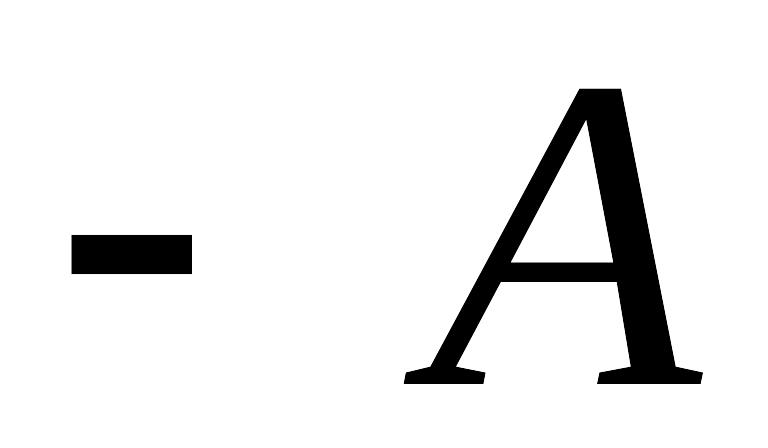 .
.
Произведением
матрицы
![]() на число
на число
![]() называется матрица, все элементы которой
равны соответствующим элементам матрицы
,
умноженным на число
называется матрица, все элементы которой
равны соответствующим элементам матрицы
,
умноженным на число
![]() .
.
Умножение матрицы на действительное число обладает следующими свойствами:
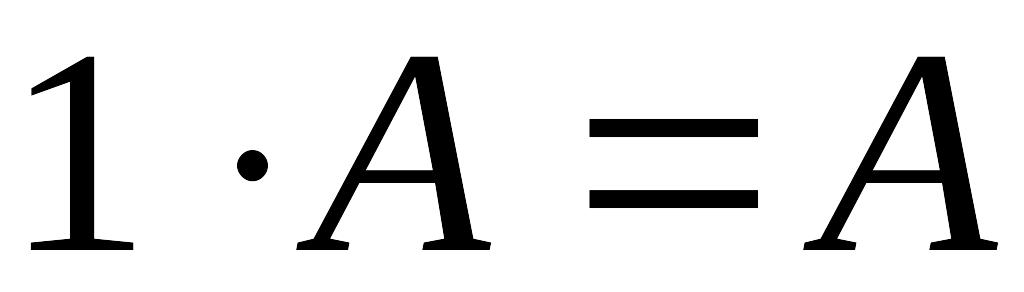 ;
;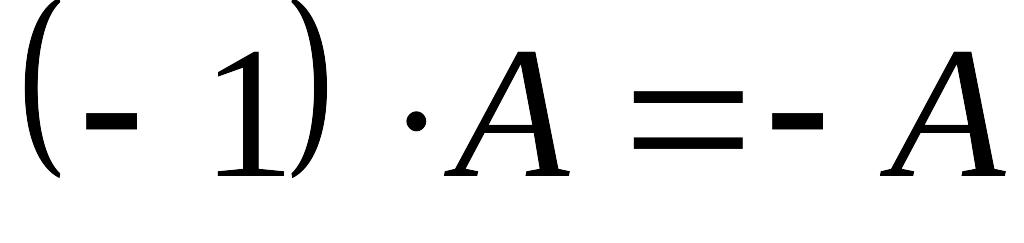 ;
;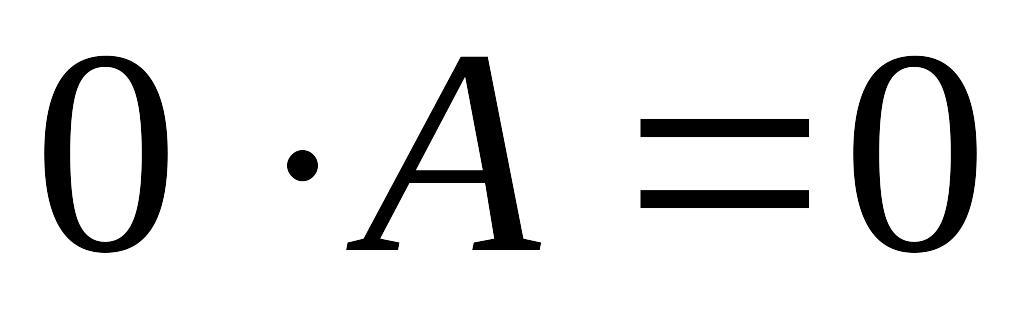 ;
;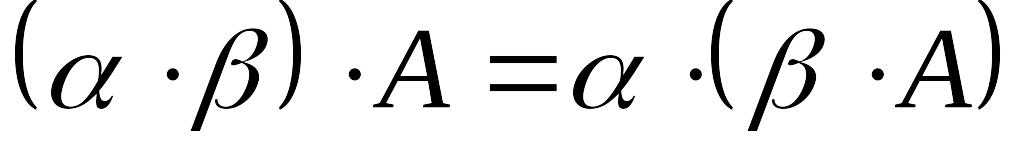 (ассоциативность);
(ассоциативность);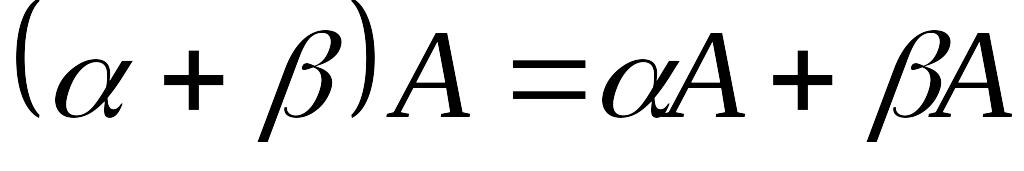 (дистрибутивность);
(дистрибутивность);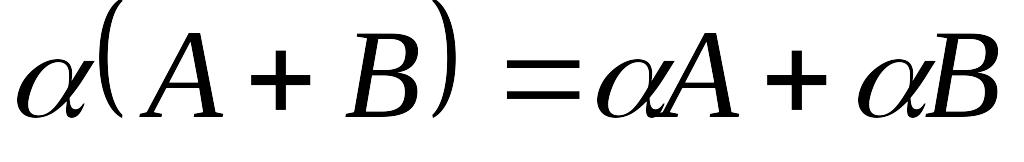 (дистрибутивность).
(дистрибутивность).
Матрица
называется согласованной
с
матрицей
,
если число столбцов матрицы
равно числу строк матрицы
.
В этом случае произведением матрицы
![]() на матрицу
на матрицу
![]() называется матрица
называется матрица
![]() ,
где
,
где
![]()
![]() ,
т.е. элемент, стоящий в
,
т.е. элемент, стоящий в
![]() -той
строке и
-той
строке и
![]() -том
столбце матрицы произведения равен
сумме произведений элементов
-той
строки матрицы
на соответствующие элементы
-го
столбца матрицы
.
-том
столбце матрицы произведения равен
сумме произведений элементов
-той
строки матрицы
на соответствующие элементы
-го
столбца матрицы
.
Свойства умножения:
Если матрица согласована с матрицей , а матрица согласована с матрицей
 ,
то
,
то
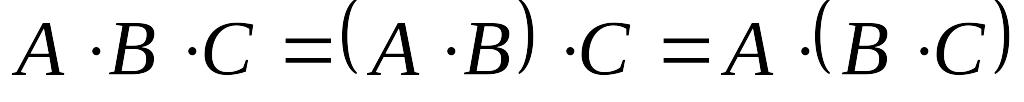 ‑ ассоциативность
умножения;
‑ ассоциативность
умножения;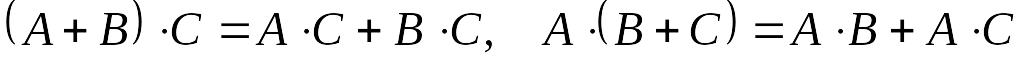 ‑
свойство
дистрибутивности;
‑
свойство
дистрибутивности;Умножение матриц не коммутативно, т.е., как правило,
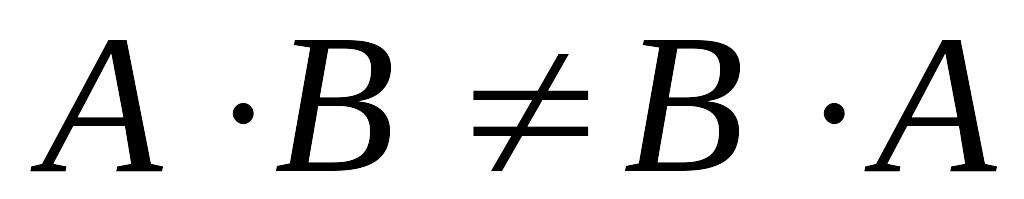 .
.
Транспонированием
матрицы
называется операция замены местами
строк и столбцов с сохранением порядка
их следования, т.е.
-я
строка матрицы
становится
-тым
столбцом транспонированной матрицы.
Матрица, транспонированная к матрице
обозначается
![]() .
.
Рангом
матрицы
называется наибольший порядок ее
миноров, отличных от нуля. Ранг матрицы
обозначают
![]() или
или
![]() .
.
Если все миноры порядка данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.
Если
все миноры первого порядка (элементы
матрицы
)
равны нулю, то
![]() .
Если хотя бы один из миноров первого
порядка отличен от нуля, а все миноры
второго порядка равны нулю, то
.
Если хотя бы один из миноров первого
порядка отличен от нуля, а все миноры
второго порядка равны нулю, то
![]() .
Причем, достаточно просмотреть только
те миноры второго порядка, которые
окаймляют ненулевой минор первого
порядка. Если найдется минор второго
порядка отличный от нуля, исследуют
миноры третьего порядка, окаймляющие
ненулевой минор второго порядка. Так
продолжают до тех пор, пока не придут к
одному из двух случаев: либо все миноры
порядка
,
окаймляющие ненулевой минор
.
Причем, достаточно просмотреть только
те миноры второго порядка, которые
окаймляют ненулевой минор первого
порядка. Если найдется минор второго
порядка отличный от нуля, исследуют
миноры третьего порядка, окаймляющие
ненулевой минор второго порядка. Так
продолжают до тех пор, пока не придут к
одному из двух случаев: либо все миноры
порядка
,
окаймляющие ненулевой минор
![]() -го
порядка равны нулю, либо таких миноров
нет. Тогда
-го
порядка равны нулю, либо таких миноров
нет. Тогда
![]() .
.
Обратная матрица.
Пусть
- квадратная матрица порядка
.
Матрица
называется обратной
матицей
к матрице
,
если выполняются равенства
![]() ,
где
‑ единичная матрица порядка
.
,
где
‑ единичная матрица порядка
.
Теорема 1. Если для данной матрицы существует обратная матрица, то она единственная.
Пусть
![]() и
и
![]() ‑ матрицы, обратные к матрице
.
Тогда
‑ матрицы, обратные к матрице
.
Тогда
![]() ,
с другой стороны,
,
с другой стороны,
![]() .
.
Откуда
![]() .
Обратную матрицу к матрице
обозначают
.
Обратную матрицу к матрице
обозначают
![]() .
.
Теорема
2.
Матрица
имеет обратную матрицу тогда и только
тогда, когда
![]() .
.
Пусть
имеет обратную матрицу. Тогда
![]() и, применяя теорему об умножении
определителей, получаем
и, применяя теорему об умножении
определителей, получаем
![]() или
или
![]() .
Следовательно,
.
.
Следовательно,
.
Пусть
.
Укажем явное выражение матрицы
через элементы матрицы
,
а именно: если
![]() ,
то:
,
то:
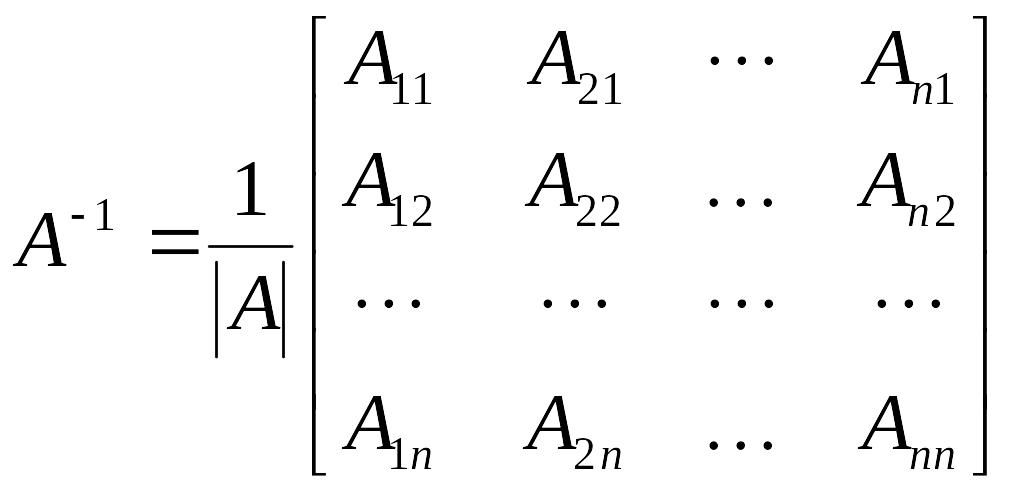
здесь
![]() ‑ алгебраическое дополнение к элементу
‑ алгебраическое дополнение к элементу
![]() .
Матрица (9.5) получается из матрицы
следующим образом. Сначала вместо
каждого элемента
пишется его алгебраическое дополнение,
затем полученная матрица транспонируется
и получается т.н. присоединенная матрица.
Для получения обратной матрицы
присоединенная матрица умножается на
величину, обратную
.
Матрица (9.5) получается из матрицы
следующим образом. Сначала вместо
каждого элемента
пишется его алгебраическое дополнение,
затем полученная матрица транспонируется
и получается т.н. присоединенная матрица.
Для получения обратной матрицы
присоединенная матрица умножается на
величину, обратную
![]() .
.
Непосредственное умножение на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) – матрица, обратная к .
Определители и их свойства.
будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое определителем матрицы и вычисляемое по определенному правилу.
Определитель
матрицы естественно возникает при
решении систем линейных уравнений, или
в свернутой форме
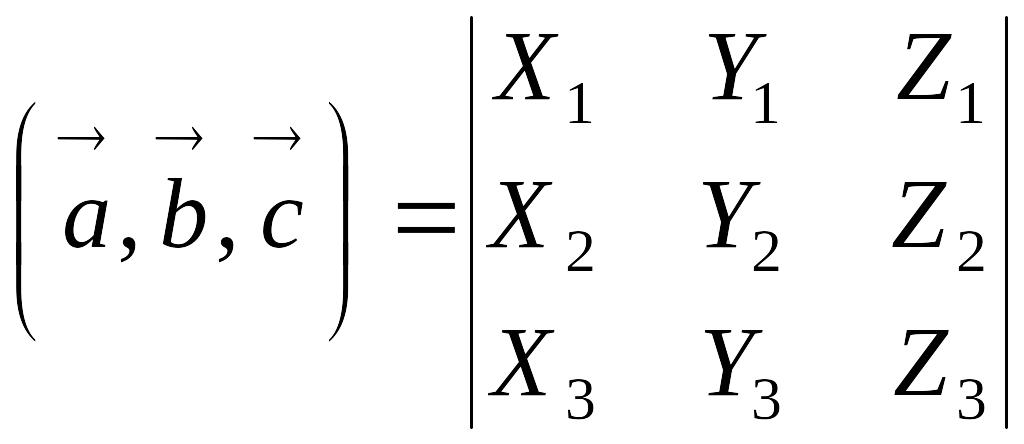 ,
или в свернутой форме
,
или в свернутой форме
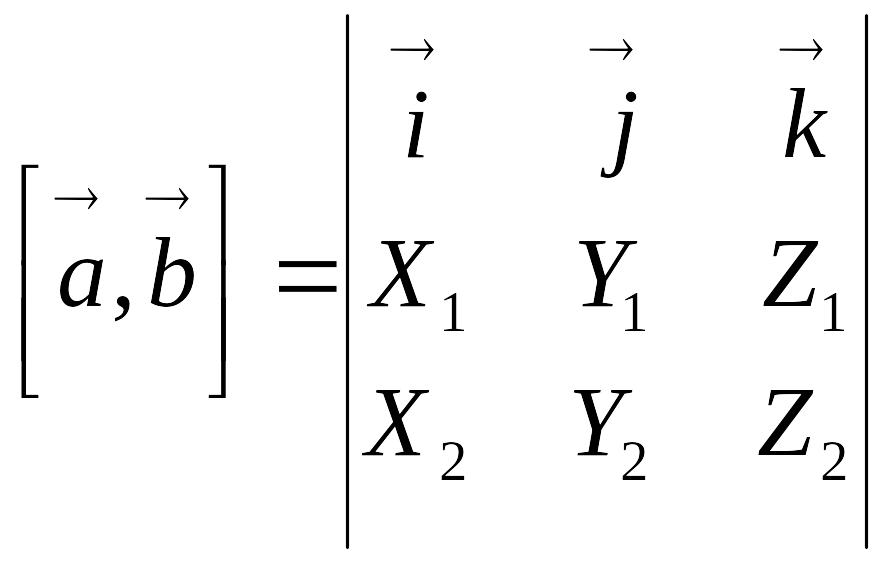 .
Предыдущая формула получается разложением
определителя по первой строке.
.
Предыдущая формула получается разложением
определителя по первой строке.
Возьмем
теперь квадратную матрицу
-го
порядка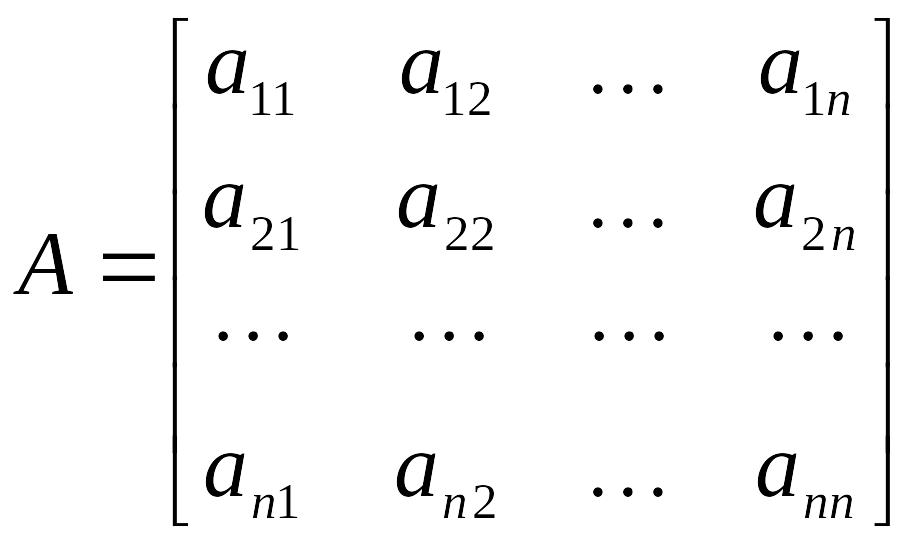
Для
записи определителя
-го
порядка матрицы
будем применять обозначения
![]() .
При
.
При
![]() матрица
состоит из одного элемента и ее
определитель равен этому элементу. При
матрица
состоит из одного элемента и ее
определитель равен этому элементу. При
![]() получаем определитель
получаем определитель
![]() .
.
Свойство 1. При транспонировании матрицы ее определитель не меняется.
Свойство 2. Если поменять местами две строки или два столбца матрицы , то ее определитель изменит знак на противоположный.
Свойство 3. Определитель, у которого две строки или два столбца одинаковы, равен нулю.
Свойство
4.
Если
все элементы какой-нибудь строки
(столбца) определителя
![]() умножить на число
,
то определитель умножится на
.
умножить на число
,
то определитель умножится на
.
Следствие 1. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
Следствие 2. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю.
Свойство 5. Определитель, у которого две строки (два столбца) пропорциональны, равен нулю.
Свойство
6.
Если каждый элемент строки (столбца)
определителя
есть сумма двух слагаемых, то определитель
равен сумме двух определителей: у одного
из них
![]() -той
строкой (столбцом)служат первые слагаемые,
а у другого – вторые.
-той
строкой (столбцом)служат первые слагаемые,
а у другого – вторые.
Свойство 7. Определитель не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Свойство 8. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали
Свойство 9. Сумма произведений элементов какой-нибудь строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.
Миноры и алгебраические дополнения.
Минором
![]() элемента
элемента
![]() матрицы
называют определитель матрицы
матрицы
называют определитель матрицы
![]() -го
порядка, получаемого из матрицы
вычеркиванием
-той
строки и
-го
столбца.
-го
порядка, получаемого из матрицы
вычеркиванием
-той
строки и
-го
столбца.
Пример.
Найти минор
![]() матрицы:
матрицы:
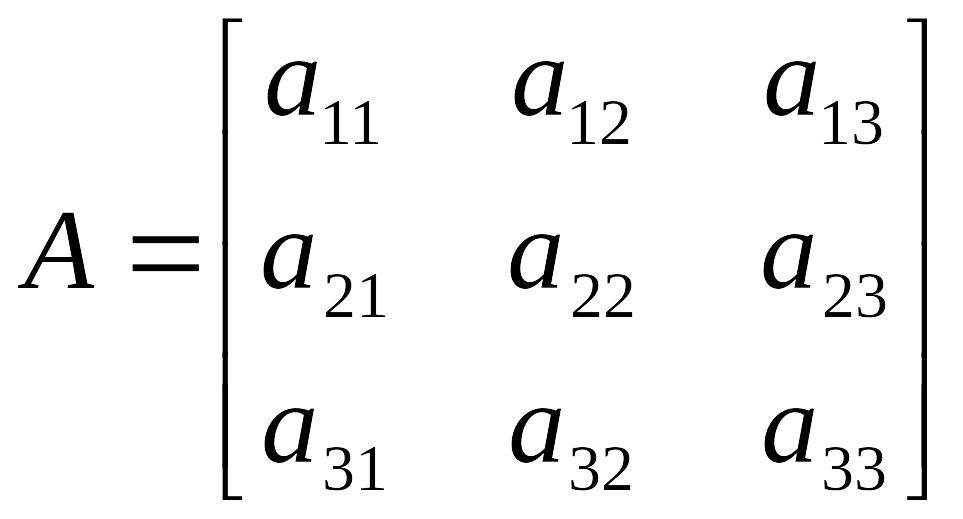 .
.
По
определению, минор
элемента
![]() есть определитель матрицы, получаемой
из матрицы
вычеркиванием первой строки и второго
столбца. Следовательно,
есть определитель матрицы, получаемой
из матрицы
вычеркиванием первой строки и второго
столбца. Следовательно,
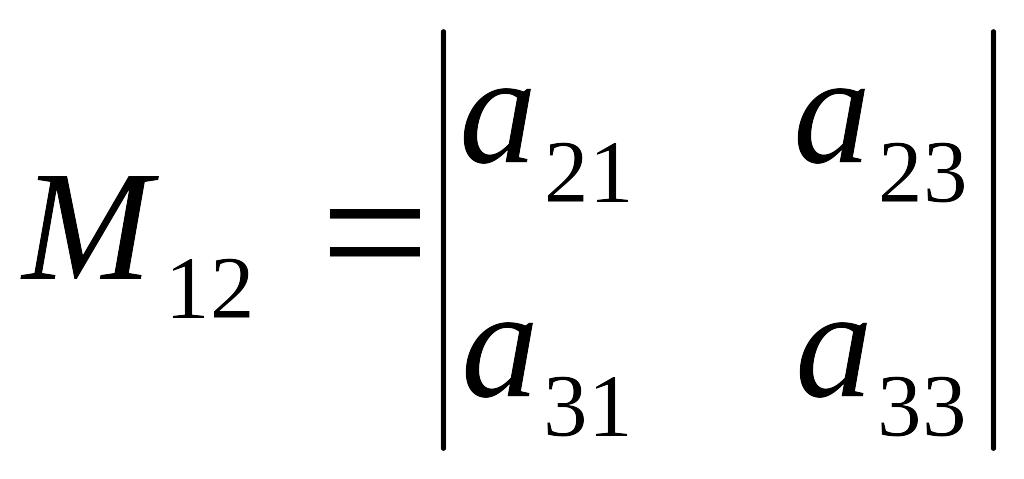 .
.
Алгебраическим
дополнением элемента
матрицы
называется минор
,
взятый со знаком
![]() .
Алгебраическое дополнение элемента
обозначается
,
следовательно,
.
Алгебраическое дополнение элемента
обозначается
,
следовательно,
![]() .
.
Алгебраическим дополнением Аij элемента аij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:
![]()
то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.
Системы линейных уравнений. Критерий совместности системы.
Система m линейных
уравнений с n неизвестными (или, линейная
система)
в линейной
алгебре — это система уравнений
вида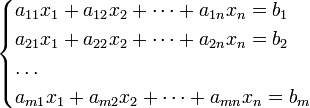
Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Система называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему обращает все её уравнения в тождества.
Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида называются различными, если нарушается хотя бы одно из равенств: c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).
Совместная система вида называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.
Матричный метод решения линейной системы.
Матричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.
Пусть дана система линейных уравнений с n неизвестными (над произвольным полем):
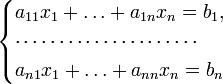
Тогда её можно переписать в матричной форме:
AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:
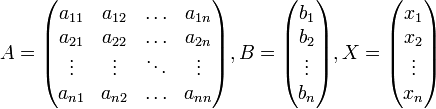
Умножим
это матричное уравнение слева на A −
1 —
матрицу, обратную к матрице A: ![]()
Так
как A −
1A = E,
получаем X = A −
1B.
Правая часть этого уравнения даст
столбец решений исходной системы.
Условием применимости данного метода
(как и вообще существования решения
неоднородной системы линейных уравнений
с числом уравнений, равным числу
неизвестных) является невырожденность матрицы
A. Необходимым и достаточным условием
этого является неравенство нулю определителя
матрицы A:
![]()
.Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть ненулевое) решение только если det A = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
Метод Гаусса–Жордана.
Метод Гаусса — Жордана (метод полного исключения неизвестных) — метод, который используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе или отыскания ранга матрицы. Метод является модификацией метода Гаусса. Назван в честь К. Ф. Гаусса и немецкого геодезиста и математика Вильгельма Йордана[1].
Выбирают первый слева столбец матрицы, в котором есть хоть одно отличное от нуля значение.
Если самое верхнее число в этом столбце есть ноль, то меняют всю первую строку матрицы с другой строкой матрицы, где в этой колонке нет нуля.
Все элементы первой строки делят на верхний элемент выбранного столбца.
Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) ноль.
Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.
После повторения этой процедуры n − 1 раз получают верхнюю треугольную матрицу
Вычитаем из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.
Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).
Чтобы получить обратную матрицу, нужно применить все операции в том же порядке к единичной матрице.
Метод Крамера.
Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевымопределителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.
Для системы n линейных уравнений с n неизвестными (над произвольным полем)
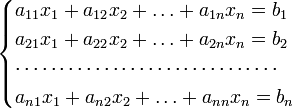
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде
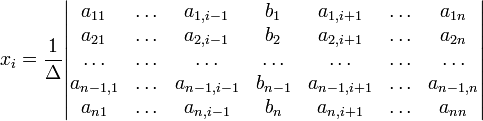
(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:
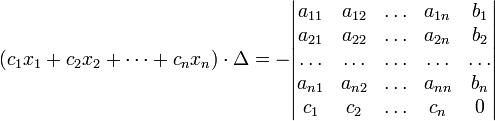
В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b1,b2,...,bn и x1,x2,...,xn, либо набор c1,c2,...,cn состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.
Векторы на плоскости и в пространстве. Линейные операции на векторах. Базисы в
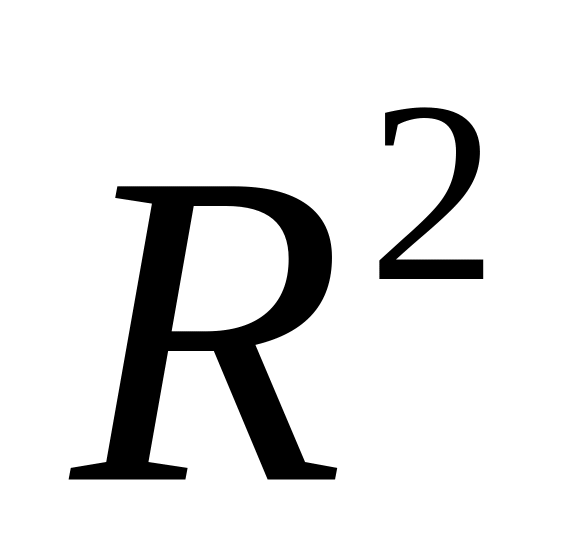 и
и
 .
Координаты вектора.
.
Координаты вектора.
Векторной величиной или вектором называется величина, для задания которой кроме численного значения необходимо указать и ее направление в пространстве, например, изменение темпов производства (рост или падение), колебание курса акций на бирже и т.д.
Векторная величина графически обычно изображается как связанный вектор или направленный отрезок, т.е. отрезок прямой, у которого указано, какая из ограничивающих точек является его началом, а какая концом. Но в отличие от направленного отрезка, для описания которого необходимо указать начальную точку, длину и направление, свободный вектор или просто вектор представляет собой множество всех эквивалентных между собой связанных векторов и вполне характеризуется:
направлением;
длиной (модулем).
Длина
вектора называется его модулем,
обозначается
![]() или
или
![]() и равна длине любого его представителя,
т.е. расстоянию между начальной и конечной
точками связного вектора
и равна длине любого его представителя,
т.е. расстоянию между начальной и конечной
точками связного вектора
![]() .
Вектор, длина которого равна нулю,
называется нуль-вектором
и обозначается
.
Вектор, длина которого равна нулю,
называется нуль-вектором
и обозначается
![]() .
.
Два вектора называются равными, если:
равны их длины;
они параллельны;
они направлены в одну сторону.
