Трёхфазные электрические цепи

С овокупность цепей, где действуют три синусоидальных ЭДС одной и той же частоты, сдвинутые по фазе (во времени) относительно друг друга.

Фазой в трёхфазной системы называется часть трёхфазной цепи, где течёт один из токов. Существуют симметричные и не симметричные системы:

, , .

Рассмотрим устройство генератора трёхфазного тока. Имеется подвижная часть – ротор, неподвижная часть – статор, в котором размещены замкнутые контура. В статор помещены три замкнутых контура, расположенные под углом друг к другу. На роторе размещается обмотка возбуждения, которая питается от отдельного источника. По этой обмотке идёт ток, который создаёт магнитное поле. Ротор вращают, при этом образуется вращательное магнитное поле, которое создаёт переменный ток.

В нешняя цепь может соединяться или звездой, или треугольником (рисунок снизу). Генератор всегда соединён звездой.

Провода, соединяющие начало фаз генератора и приёмника, называются линейными. Напряжение, возникающее между началом и концом фазы, называется фазным.

.

М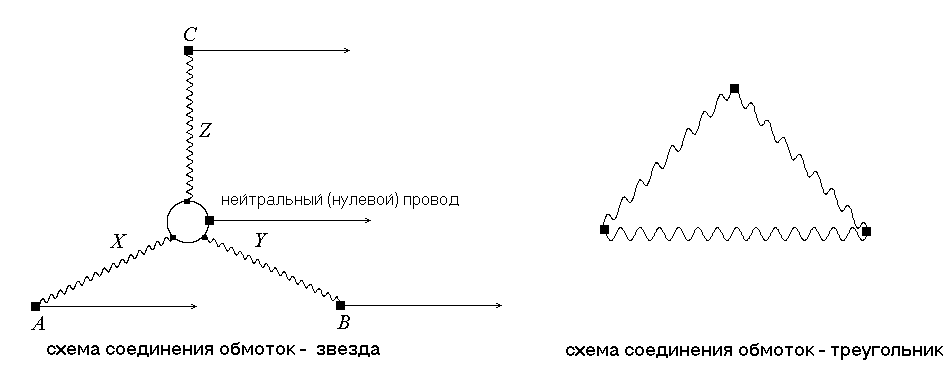 ощность трёхфазной системы при соединении её треугольником в три раза больше, чем мощность в этих же элементах, соединённых звездой.

Уравнения Максвелла

Уравнения Максвелла не выводятся. Они обобщают существующую теорию. Максвелл выдвинул гипотезу о существовании единого электромагнитного поля, которое меняется во времени и в пространстве, которое может существовать в виде электромагнитных волн, которые распространяются в вакууме с постоянной скоростью, равной скорости света.

Симметрия нарушена из-за отсутствия в природе магнитных зарядов.

Уравнения справедливы как для однородных, так и для неоднородных сред, а также на границах раздела. Уравнения – для неферромагнитных однородных сред. Существуют в двух формах: интегральной и дифференциальной. Дифференциальная форма предполагает, что величины в правой и левой части уравнения относятся к одной и той же точке.

1-е уравнение Максвелла

Является обобщением закона полного тока. Напомним закон полного тока: , где - упорядоченное движение зарядов, - ток, возникающий из-за изменения напряженности электрического поля . . Т.о., запишем 1-е уравнение в интегральной форме:

.

В пределе: - уравнение в дифференциальной форме.

Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

2-е уравнение Максвелла

Является обобщением закона электромагнитной индукции Фарадея.

,

( - работа вдоль замкнутой кривой), т.е. изменяющееся во времени магнитное поле является источником вихревого электрического поля (т.к. если электрическое поле не вихревое, то ).

- уравнение в интегральной форме (т.е. правая и левая части уравнения, вообще говоря, относятся к различным точкам пространства).

Чтобы перейти к дифференциальной форме, используем формулу Стокса:

- уравнение в дифференциальной форме.

Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

3-е уравнение Максвелла

Является обобщением теоремы Остроградского-Гаусса.

,

т.е. поток через замкнутую поверхность равен сумме зарядов в объеме, ограниченной . Это уравнение в интегральной форме. Здесь - объемная плотность заряда.

,

уравнение в дифференциальной форме.

4-е уравнение Максвелла

Теорема Остроградского-Гаусса применительно к магнитным полям:

,

так как не существует магнитных зарядов.

Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):

где и - соответственно электрическая и магнитная постоянные, и - соответственно диэлектрическая и магнитная проницаемости, - удельная проводимость вещества.

Недостаток уравнений Максвелла: уравнения не описывают, откуда и как берутся поля.

Из уравнений Максвелла следует существование электромагнитных волн, которые распространяются в вакууме со скоростью света:

.