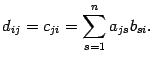- •Определители поля. Примеры поля комплексных чисел?
- •Алгебраическая запись комплексного числа. Операции над комплексными числами, их св-ва?
- •Сопряжения и его свойства?
- •4.Модуль и аргумент комплексного числа, их свойства. Тригонометрическая форма записи числа. Формула муравла.
- •Извлечение корня n-степени из комплексного числа?
- •6.Многочлены. Деление многочленов с остатком?
- •7.Теорема Декарта-Безу, схема Горнера. Пример
- •Доказательство
- •8. Рациональные корни многочлена с целыми коэффициентами. Пример. Основная теорема алгебры. Рациональные корни многочленов с целыми коэффициентами
- •Следствие
- •Действительная функция комплексного переменного f(X) непрерывная в замкнутом круге е достигает своего минимума и максимума.
- •Предположим, что это не верно тогда
- •9. Матрицы. Сложение матриц, умножение матриц на число, их свойства.
- •Умножение матрицы на число
- •Свойства умножения матрицы на число
- •10. Умножение матриц, свойства. Пример.
- •11. Транспонирование матриц, свойства. Обратная матрица и её свойства. Транспонирование матриц
- •Транспонирование матрицы
- •Обратная матрица
- •12.Элементарные преобразования строк и столбцов матриц, их матричная интерпретация.
- •18. Алгебраические дополнения элементов матрицы. Разложения определителя по строке.
- •23.Невырожденная матрица. Теорема о существовании обратной матрицы.
- •25. Пространство решений однородной слу. Фундаментальная система решений.
- •27.Структура множества решений слу. Способы решений. Методы решения систем линейных алгебраических уравнений
- •Постановка задачи
- •Правило Крамера
- •Условие совместности системы линейных уравнений
- •28. Пространство геометрических векторов. Операции с векторами и свойства.
- •29. Коллиниарность, комплонарность и линейная зависимость векторов.
- •Линейная зависимость векторов
- •30. Проекция вектора на ось, свойства.
- •31. Скалярное произведение. Критерий ортогональности векторов. Алгебраические свойства скалярного произведения. Скалярное произведение векторов
- •32. Ортонормированный базис. Выражение скалярного произведения через координаты векторов. Длина вектора и угол между ними. Пример.
- •Скалярное произведение векторов в ортонормированном базисе
- •Длина вектора Понятие вектора
- •33. Определение векторного и смешенного произведения векторов. Критерии комплонарности и колинеарности векторов в координатной форме. Площадь паралеограма и объём параллелепипеда.
- •34.Свойство векторного и смешенного произведения. Геометрические свойства векторного произведения Править
- •Алгебраические свойства векторного произведения Править
- •Выражение для векторного произведения в декартовых координатах Править
- •Свойства
- •35.Выражение векторного и смешенного произведения через координаты векторов.
- •8.4. Некоторые приложения смешанного произведения
- •36.Пдск. Координаты точки и координаты векторов. Преобразование координат при переходе к другой пдск.
- •Система координат и координаты вектора
- •37. Пск. Формулы перехода в пдск. Другие системы координат. Полярные координаты
- •[Править]Цилиндрические координаты
- •[Править]Сферические координаты
- •[Править]Обозначения, принятые в Америке
- •[Править]Европейские обозначения
- •38. Понятие об уравнении фигуры. Объединение пересечение фигур.
- •39. Уравнения примой на плоскости.
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •40. Уравнение плоскости.
- •41. Уравнение прямой в пространстве.
- •42. Угол между прямыми, плоскостями, прямой и плоскостью. Пример. Угол между прямыми на плоскости
- •Угол между плоскостями
- •43. Расстояние от точки до прямой, от точки до плоскости, между прямыми, между плоскостями. Пример. Расстояние от точки до прямой
- •Расстояние от точки до плоскости
- •44. Эллипс. Директрисы и оптические свойства гиперболы. Ллипс
- •46. Парабола. Парабола
- •47. Линейный оператор. Матрица линейного оператора.
- •48. Собственные числа, собственные векторы. Собственные числа и собственные векторы линейного оператора
- •49. Привидение в квп к каноническому виду.
- •50. Поверхности второго порядка. Метод сечений. Поверхности второго порядка
Умножение матрицы на число
Произведением матрицы A = (aij) размера m×n и вещественного числа α называется матрица того же размера C = (cij), элементы которой определяется формулой
cij = αaij (i = 1, …, m, j = 1, …, n) |
То, что матрица C является результатом умножения матрицы A на число α, записывается в виде C = αA.
Свойства умножения матрицы на число
Для любой матрицы A и любых чисел α, β R:
1·A = A;
α(βA) = (αβ)A;
Оерации сложения матриц и умножения матрицы на число согласованы следующим образом. Для любых матриц A и B одного и того же размера и любых чисел α, β R:
(α + β)A = αA + βA;
α(A + B) = αA + αB.
Операции сложения и умножения на число называют линейными операциями.
10. Умножение матриц, свойства. Пример.
Умножать друг на друга можно только те матрицы, для которых число столбцов первого сомножителя равно числу строк второго сомножителя. Результатом умножения является матрица, у которой число строк равно числу строк первого сомножителя, а число столбцов совпадает с числом столбцов второго сомножителя.
Пример. ![]()
Иными словами, перемножать можно те матрицы, у которых совпадают средние индексы. Крайние индексы определяют размерность получаемого результата
![]()
Элемент ci,j матрицы – ответа принадлежащий i-ой строке и j-му столбцу, вычисляется как произведение i-ой строки первого сомножителя An,m на j-ый столбец второго сомножителяBm,k. Так, например, при вычислении элемента умножается первая строка на третий столбец, а при вычислении элемента умножается третья строка на первый столбец.
Можно перемножать только те строки и столбцы, у которых одинаковое число элементов (смотри условие возможности умножения матриц). В результате получается число, равное сумме произведений соответствующих элементов (первый элемент строки на первый элемент столбца плюс второй элемент строки на второй элемент столбца и т. д. и, наконец, плюс произведение последних элементов).
Рассмотрим умножение матриц на примере :
![]()
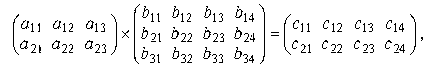
где
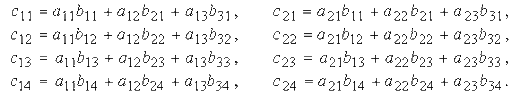
Пример. 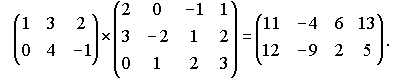
Отметим основные свойства операции произведения матриц.
1) В общем случае ![]() .
Если
.
Если ![]() то
матрицы А и Вназываются
перестановочными по отношению друг к
другу.
то
матрицы А и Вназываются
перестановочными по отношению друг к
другу.
2) ![]()
3) ![]()
4)
При умножении любой квадратной матрицы
на единичную первоначальная матрица
не меняется ![]()
11. Транспонирование матриц, свойства. Обратная матрица и её свойства. Транспонирование матриц
Если в матрице Аmn поменять местами строки и столбцы, получим транспонированную матрицу Anmт.
Пример.

Свойства транспонирования:
(Ат)т = А; (А + В)т = Ат + Вт; (А В С)т = СтВтАт - транспонированное произведение матриц равно произведению транспонированных матриц, записанных в обратной последовательности. Если А = Ат, матрица симметрична.
Транспонирование матрицы
Над матрицами определена еще одна операция, называемая транспонированием.
Определение 14.5
Пусть ![]() --
матрица размеров
--
матрица размеров ![]() .
Тогда транспонированной
матрицей
называется
такая матрица
.
Тогда транспонированной
матрицей
называется
такая матрица ![]() размеров
размеров ![]() ,
что
,
что ![]() ,
, ![]() ,
, ![]() .
.
Транспонированная
матрица
обозначается ![]() или
или ![]() .
Операция транспонирования заключается
в том, что строки и столбцы в исходной
матрице меняются ролями. В транспонированной
матрице первым столбцом служит первая
строка исходной матрицы, вторым
столбцом -- вторая строка исходной
матрицы и т.д. Например,
.
Операция транспонирования заключается
в том, что строки и столбцы в исходной
матрице меняются ролями. В транспонированной
матрице первым столбцом служит первая
строка исходной матрицы, вторым
столбцом -- вторая строка исходной
матрицы и т.д. Например,
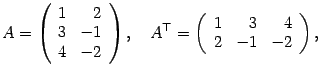

Читатель легко проверит, что
![]()
где ![]() --
число.
--
число.
Предложение 14.5 Если
произведение ![]() определено,
то
определено,
то
|
(14.8) |
Доказательство.
Пусть
--
матрица размеров
,
--
матрица размеров ![]() .
Тогда
имеет
размеры
,
.
Тогда
имеет
размеры
, ![]() --
размеры
--
размеры ![]() .
Число столбцов в
совпадает
с числом строк в
,
поэтому произведение
на
определено.
Размеры этого произведения
.
Число столбцов в
совпадает
с числом строк в
,
поэтому произведение
на
определено.
Размеры этого произведения ![]() .
Матрица
имеет
размеры
.
Матрица
имеет
размеры ![]() ,
поэтому
,
поэтому ![]() --
матрица размеров
.
Итак, матрицы в правой и левой части
равенства (14.8)
существуют и имеют одинаковые размеры.
--
матрица размеров
.
Итак, матрицы в правой и левой части
равенства (14.8)
существуют и имеют одинаковые размеры.
Пусть ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
Нам нужно показать, что
.
Нам нужно показать, что ![]() ,
, ![]() ,
.
,
.
По определению
транспонирования ![]() .
По определению умножения матриц
.
По определению умножения матриц
|
(14.9) |
С другой стороны,
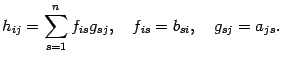
Поэтому

Сравнивая полученный результат с (14.9), получаем .