Длина вектора Понятие вектора
Отрезок,
для которого указано, какой из его концов
считается началом, а какой — концом,
называется вектором.
Направление вектора (от начала к концу)
на рисунках отмечается стрелкой. Любая
точка пространства также может
рассматриваться как вектор. Такой вектор
называется нулевым.
Начало и конец нулевого вектора совпадают,
и он не имеет какого-либо определенного
направления. Нулевой вектор обозначается
символом 
Длиной
ненулевого вектора 
называется
длина отрезка AB. Длина вектора
(вектора 
)
обозначается так: 
.
Длина нулевого вектора считается равной
нулю: 
.
Два
ненулевых вектора называются коллинеарными,
если они лежат на одной прямой ил на
параллельных прямых. Если два ненулевых
вектора
и 
коллинеарны
и если при этом лучи AB и CD сонаправлены,
то векторы
и
называются сонаправленными,
а если эти лучи не являются сонаправленными,
то векторы
и
называютсяпротивоположно
направленными.
Нулевой вектор принято считать
сонаправленным с любим вектором.
гол между векторами. Угол между вектором и осью.
Определение. Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один извекторов вокруг своего начала до положения сонаправленности с другим вектором.
рис.1.
Обозначение. 
.
Из определения следует,
что 
.
Мы полагаем очевидным, что при параллельном переносе любого издвух векторов угол между ними остается неизменным, только в этом случае поворот одного из векторов осуществляется либо в общей для обоих векторов плоскости, либо в плоскости параллельной другому вектору.
Введем понятие угла между вектором и осью.
Определение. Углом между вектором и осью называется угол между данным вектором и любым правоориентированным вектором этой оси.
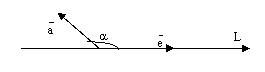
рис.2.
Обозначение. 
.
33. Определение векторного и смешенного произведения векторов. Критерии комплонарности и колинеарности векторов в координатной форме. Площадь паралеограма и объём параллелепипеда.
Векторное произведение векторов.
Определение.
Векторным произведением вектора
на
вектор 
называется
третий вектор 
,
который удовлетворяет следующим трем
условиям:
1) 
и 
;
2)
тройка векторов 
является
правоориентированной;
3) 
.
рис.2.
Обозначение: 
.
Из определения следует, что, если векторы , и отложить от одной точки, то
1) вектор перпендикулярен плоскости, в которой лежат векторы и ;
2) кратчайший поворот вектора к вектору происходит против часовой стрелки, если смотреть "сверху", т.е. со стороны вектора ;
3) длина вектора численно равна площади параллелограмма, построенного на векторах и , как на его сторонах.
Теорема. (Свойства векторного произведения.)
1). Антикоммутативность:
, 
.
2). Условие коллинеарности векторов:
.
3). Модуль векторного произведения численно равен площади параллелограмма, построенного на векторах и , как на его сторонах.
Доказательство.
1) Пусть 
.
Рассмотрим вектор 
.
Этот вектор удовлетворяет всем трем
условиям определения векторногопроизведения вектора
на
вектор
.
Действительно,
т.к.
и
,
то и 
и 
.
Далее, тройка векторов 
является
правоориентированной, т.е. кратчайший
поворот от вектора
к
вектору
происходит
против часовой стрелки, если смотреть
на плоскость, в которой
лежат векторы
и
"снизу",
т.е. со стороны вектора
.
И,
наконец, 
,
ч.т.д.
2)
Если один из векторов или оба равны
нулю, то они коллинеарные и их векторное
произведение равно нулевому вектору,
тут все очевидно. Пусть векторы
и
ненулевые.
Тогда 
или 
,
а это в свою очередь равносильно тому,
что 
,
ч.т.д.
3) Следует из формулы площади параллелограмма.
Теорема доказана.
Смешанное произведение векторов.
Определение.
Смешанным произведением упорядоченной
тройки векторов 
называется скалярное произведение
первого вектора навекторное произведение
второго вектора на
третий и обозначается
.
Теорема. (Геометрический смысл смешанного произведения.)
1) Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на трех данных векторах, как на его ребрах:
.
2) 
,
если тройка 
–
правоориентированная и 
в
противном случае.
Доказательство.
1) Обозначим через 
объем
параллелепипеда, построенного на данных
векторах, как на его ребрах.
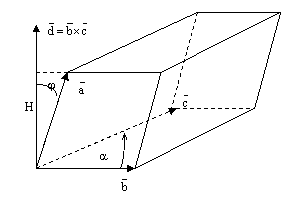
рис.3.
Объем
параллелепипеда V равен произведению
площади основания S на высоту Н: 
.
Площадь
основания S численно равна
модулю векторногопроизведения: 
,
а высота Н равна модулю проекции вектора
на
вектор 
:
.
Отсюда получаем:
,
ч.т.д.
2)
Так как 
,
где 
,
то знак смешанного произведениязависит
от угла 
.
Если он острый, то смешанное
произведение
и
,
если угол
–
тупой. А это зависит, в свою очередь, от
ориентации тройки векторов
.
На рисунке 3 изображена правая тройка
векторов
.
Если смотреть со стороны третьего вектора
,
то кратчайший поворот первого вектора
ко
второму
осуществляется
против часовой стрелки. В этом
случае угол
–
острый и
.
Если же тройка
–
левая, то конец вектора
будет
лежать нижеплоскости векторов
и
(по
сравнению с рис.3) и угол
будет
тупым и
,
ч.т.д.
Теорема доказана.
Будем
говорить, что тройки векторов 
и 
получились
из тройки
с помощью круговой
перестановки векторов. В первом случае
третий вектор
переставляется
на первое место, а векторы
и
сдвигаются
вправо на второе и
третье места соответственно. Во втором
случае, первый вектор
переставляется
на третье место, авекторы
и
сдвигаются
влево на первое и второе места
соответственно. Заметим, что при круговой
перестановке векторов ни один из них
не остается на своем месте.
Если
же в тройке векторов меняются местами
только два вектора, а один из векторов
остается на своем месте, то такую
перестановку мы будем называть не
круговой перестановкой (или транспозицией).
Так тройки 
, 
, 
получаются
из тройки
транспозицией
векторов. Так, например, в тройке
остался
на третьем месте вектор
.
Любую тройку векторов можно упорядочить 6-ю способами. Из них три тройки будут правыми и три тройки будут левыми.
Если тройка правая (как на рис.3), то правыми будут и тройки полученные из нее круговой перестановкой: и . В то же время, тройка будет левой и левой же будут тройки, полученные из нее круговой перестановкой: и .
Лемма. Круговая перестановка в тройке векторов не изменяет ее ориентации, а транспозиция векторов изменяет ориентацию тройки на противоположную.
Доказательство проведите самостоятельно с использованием соответствующих картинок.
1) 
;
2) 
;
3) 
.
Доказательство. 1) По модулю все эти смешанные произведения равны друг другу, т.к. параллелепипед, построенный на данных трех векторах, как его ребрах, не зависит от того, в каком порядке мы записываем его ребра и, соответственно, не изменяется его объем.
2) Знак смешанного произведения упорядоченной тройки векторов зависит от ее ориентации, которая не меняется при круговой перестановке и меняется при транспозиции, откуда и следуют доказываемые равенства.
3) Воспользуемся уже доказанным равенством, определением смешанного произведения и свойством коммутативности скалярногопроизведения:
.
Следствие доказано.