
- •Определители поля. Примеры поля комплексных чисел?
- •Алгебраическая запись комплексного числа. Операции над комплексными числами, их св-ва?
- •Сопряжения и его свойства?
- •4.Модуль и аргумент комплексного числа, их свойства. Тригонометрическая форма записи числа. Формула муравла.
- •Извлечение корня n-степени из комплексного числа?
- •6.Многочлены. Деление многочленов с остатком?
- •7.Теорема Декарта-Безу, схема Горнера. Пример
- •Доказательство
- •8. Рациональные корни многочлена с целыми коэффициентами. Пример. Основная теорема алгебры. Рациональные корни многочленов с целыми коэффициентами
- •Следствие
- •Действительная функция комплексного переменного f(X) непрерывная в замкнутом круге е достигает своего минимума и максимума.
- •Предположим, что это не верно тогда
- •9. Матрицы. Сложение матриц, умножение матриц на число, их свойства.
- •Умножение матрицы на число
- •Свойства умножения матрицы на число
- •10. Умножение матриц, свойства. Пример.
- •11. Транспонирование матриц, свойства. Обратная матрица и её свойства. Транспонирование матриц
- •Транспонирование матрицы
- •Обратная матрица
- •12.Элементарные преобразования строк и столбцов матриц, их матричная интерпретация.
- •18. Алгебраические дополнения элементов матрицы. Разложения определителя по строке.
- •23.Невырожденная матрица. Теорема о существовании обратной матрицы.
- •25. Пространство решений однородной слу. Фундаментальная система решений.
- •27.Структура множества решений слу. Способы решений. Методы решения систем линейных алгебраических уравнений
- •Постановка задачи
- •Правило Крамера
- •Условие совместности системы линейных уравнений
- •28. Пространство геометрических векторов. Операции с векторами и свойства.
- •29. Коллиниарность, комплонарность и линейная зависимость векторов.
- •Линейная зависимость векторов
- •30. Проекция вектора на ось, свойства.
- •31. Скалярное произведение. Критерий ортогональности векторов. Алгебраические свойства скалярного произведения. Скалярное произведение векторов
- •32. Ортонормированный базис. Выражение скалярного произведения через координаты векторов. Длина вектора и угол между ними. Пример.
- •Скалярное произведение векторов в ортонормированном базисе
- •Длина вектора Понятие вектора
- •33. Определение векторного и смешенного произведения векторов. Критерии комплонарности и колинеарности векторов в координатной форме. Площадь паралеограма и объём параллелепипеда.
- •34.Свойство векторного и смешенного произведения. Геометрические свойства векторного произведения Править
- •Алгебраические свойства векторного произведения Править
- •Выражение для векторного произведения в декартовых координатах Править
- •Свойства
- •35.Выражение векторного и смешенного произведения через координаты векторов.
- •8.4. Некоторые приложения смешанного произведения
- •36.Пдск. Координаты точки и координаты векторов. Преобразование координат при переходе к другой пдск.
- •Система координат и координаты вектора
- •37. Пск. Формулы перехода в пдск. Другие системы координат. Полярные координаты
- •[Править]Цилиндрические координаты
- •[Править]Сферические координаты
- •[Править]Обозначения, принятые в Америке
- •[Править]Европейские обозначения
- •38. Понятие об уравнении фигуры. Объединение пересечение фигур.
- •39. Уравнения примой на плоскости.
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •40. Уравнение плоскости.
- •41. Уравнение прямой в пространстве.
- •42. Угол между прямыми, плоскостями, прямой и плоскостью. Пример. Угол между прямыми на плоскости
- •Угол между плоскостями
- •43. Расстояние от точки до прямой, от точки до плоскости, между прямыми, между плоскостями. Пример. Расстояние от точки до прямой
- •Расстояние от точки до плоскости
- •44. Эллипс. Директрисы и оптические свойства гиперболы. Ллипс
- •46. Парабола. Парабола
- •47. Линейный оператор. Матрица линейного оператора.
- •48. Собственные числа, собственные векторы. Собственные числа и собственные векторы линейного оператора
- •49. Привидение в квп к каноническому виду.
- •50. Поверхности второго порядка. Метод сечений. Поверхности второго порядка
6.Многочлены. Деление многочленов с остатком?
Многочлен или полином (от греч. «поли» - много и лат. «номен» - имя) – класс элементарных функций классической алгебры и алгебраической геометрии. Это функция одной переменной, которая имеет вид F(x) = c_0 + c_1*x + … + c_n*x^n, где c_i – фиксированные коэффициенты, x – переменная.
Многочлены применяются во многих разделах, в том числе рассмотрении нуля, отрицательных и комплексных чисел, теории групп, колец, узлов, множеств и т.д. Использование полиномиальных вычислений значительно упрощает выражение свойств разных объектов.
Основные определения многочлена: • Каждое слагаемое полинома называется одночленом или мономом. • Многочлен, состоящий из двух одночленов, называют двучленом или биномом. • Коэффициенты полинома – вещественные или комплексные числа. • Если старший коэффициент равен 1, то многочлен называют унитарным (приведенным). • Степени переменной в каждом одночлене – целые неотрицательные числа, максимальная степень определяет степень многочлена, а его полной степенью называется целое число, равное сумме всех степеней. • Одночлен, соответствующий нулевой степени, называется свободным членом. • Многочлен, все одночлены которого имеют одинаковую полную степень, называется однородным.
Определение. Пусть ![]() и
и ![]() — многочлены,
— многочлены, ![]() .
Будем говорить, что
поделен
на
с
остатком, если
представлен
в виде
.
Будем говорить, что
поделен
на
с
остатком, если
представлен
в виде ![]() ,
где
,
где ![]() и
и ![]() —
многочлены, причем
—
многочлены, причем ![]() .
.
Полином называется остатком от деления на , — неполным частным.
Пример. ![]() .
.
![]() .
.
Теорема. (о
делении с остатком). Пусть
и
—
полиномы над полем ![]() ,
.
Тогда существуют единственные
многочлены
и
над
полем
такие,
что
,
.
Тогда существуют единственные
многочлены
и
над
полем
такие,
что ![]() и
.
и
.
Доказательство. Существование.
Пусть ![]() .
Положим
.
Положим ![]() .
.
![]() .
.
Предположим,
что теорема верна не для любого
полинома
(
фиксируем).
Среди всех многочленов
,
для которых теорема неверна, выберем
многочлен наименьшей степени и обозначим
его ![]() :
:
![]()
Пусть ![]() .
Положим
.
Положим
![]()
Коэффициент
при ![]() в
многочлене
в
многочлене ![]() равен
равен ![]() .
Следовательно,
.
Следовательно, ![]() .
Значит, для многочлена
теорема
верна. Существуют такие
.
Значит, для многочлена
теорема
верна. Существуют такие ![]() и
,
что
и
,
что ![]() .
Тогда
.
Тогда

Получили противоречие с тем предположением, что есть многочлены, для которых теорема неверна.
Единственность.
Предположим, что
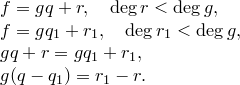
1) ![]() .
Значит,
.
Значит, ![]() ,
,
2) ![]() .
.
![]() Получили
противоречие. Этот случай невозможен.
Получили
противоречие. Этот случай невозможен.
7.Теорема Декарта-Безу, схема Горнера. Пример
Теорема Безу утверждает, что остаток от деления многочлена P(x) на двучлен x − a равен P(a).
Предполагается, что коэффициенты многочлена содержатся в некотором коммутативном кольце с единицей (например, в поле вещественных или комплексных чисел).
Доказательство
Поделим с остатком многочлен P(x) на многочлен x − a:
P(x) = (x − a)Q(x) + R(x).
Так как deg R(x) < deg(x − a) = 1, то R(x) — многочлен степени не выше 0. Подставляя x = a, поскольку (a − a)Q(a) = 0, имеем P(a) = R(a).
Схема
Горнера - один из простейших способов
деления многочлена ![]() на
бином x-a. Конечно, делением применение
схемы Горнера не исчерпывается, но для
начала рассмотрим именно это. Применение
алгоритма поясним на примерах.
Разделим
на
бином x-a. Конечно, делением применение
схемы Горнера не исчерпывается, но для
начала рассмотрим именно это. Применение
алгоритма поясним на примерах.
Разделим ![]() на
на ![]() .
Составим таблицу из двух строк: в первой
строке запишем коэффициенты многочлена
по
убыванию степеней переменной. Заметьте,
что данный многочлен не содержит х, т.е.
коэффициент перед х равен 0. Так как мы
делим на
,
во второй строке запишем единицу:
.
Составим таблицу из двух строк: в первой
строке запишем коэффициенты многочлена
по
убыванию степеней переменной. Заметьте,
что данный многочлен не содержит х, т.е.
коэффициент перед х равен 0. Так как мы
делим на
,
во второй строке запишем единицу:
![]()
Начнем заполнять пустые ячейки во второй строке. В первую пустую ячейку запишем 5, просто перенеся ее из соответствующей ячейки первой строки:
![]()
Следующую
ячейку заполним по такому принципу: ![]()
![]()
Аналогично
заполним и четвертую: ![]() :
:
![]()
Для
пятой ячейки получим ![]() :
:
![]()
И,
наконец, для последней, шестой ячейки,
имеем ![]() :
:
![]()
Задача решена, осталось только записать ответ:
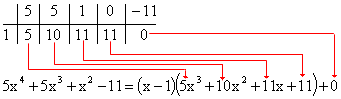
Как
видите, числа, расположенные во второй
строке (между первым и последним), есть
коэффициенты многочлена, полученного
после деления
на
.
Последнее число во второй строке означает
остачу от деления или, что то же самое,
значение многочлена
при ![]() .
Следовательно, если в нашем случае
остача равна нулю, то многочлены делятся
нацело.
.
Следовательно, если в нашем случае
остача равна нулю, то многочлены делятся
нацело.
![]()
Полученный результат говорит также и о том, что 1 является корнем многочлена .
Приведем
еще один пример. Разделим многочлен ![]() на
на ![]() .
Сразу оговорим, что выражение
нужно
представить в форме
.
Сразу оговорим, что выражение
нужно
представить в форме ![]() .
В схеме Горнера будет учавствовать
именно -3.
.
В схеме Горнера будет учавствовать
именно -3.

Если
наша цель - найти все корни многочлена,
то схему Горнера можно применять
несколько раз подряд, - до тех пор, пока
мы не исчерпаем все корни. Например,
отыщем все корни многочлена ![]() .
Целые корни нужно искать среди делителей
свободного члена, т.е. среди делителей
8. Т.е., целыми корнями могут быть числа
-8, -4, -2, -1, 1, 2, 4, 8. Проверим, к примеру, 1:
.
Целые корни нужно искать среди делителей
свободного члена, т.е. среди делителей
8. Т.е., целыми корнями могут быть числа
-8, -4, -2, -1, 1, 2, 4, 8. Проверим, к примеру, 1:
![]()
Итак, в остаче имеем 0, т.е. единица действительно является корнем данного мнгогочлена. Попробуем проверить единицу еще несколько раз. Новую таблицу для этого создавать не будем, а продолжим использование предыдущей:

Вновь в остаче ноль. Продолжим таблицу до тех пор, пока не исчерпаем все возможные значения корней:
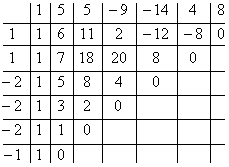
Итог: ![]() .
.
Конечно, данный метод подбора малоэффективен в общем случае, когда корни не являются целыми числами, но для целых корней метод довольно-таки неплох.
