8.4. Некоторые приложения смешанного произведения

Определение взаимной ориентации векторов в пространстве

Определение взаимной ориентации векторов а, b и с основано на следующих соображениях. Если abc > 0 , то а , b , с — правая тройка; если abc <0 , то а, b , с - левая тройка.

Установление компланарности векторов

Векторы а, b и с компланарны тогда и только тогда, когда их смешанное произведение равно нулю

  

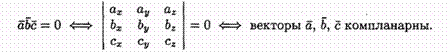
Определение объемов параллелепипеда и треугольной пирамиды

Нетрудно показать, что объем параллелепипеда, построенного на векторах а, b и свычисляется как V =|аbс|, а объем треугольной пирамиды, построенной на этих же векторах, равен V =1/6*|abc |.

Пример 6.3.

Вершинами пирамиды служат точки А(1; 2; 3), В(0; -1; 1), С(2; 5; 2) и D (3; 0; -2). Найти объем пирамиды.

Решение: Находим векторы  а,b ис:

а=AB =(-1;-3;-2),  b =АС=(1;3;-1),   с=AD =(2; -2; -5).

Находима, b и с:

    =-1•(-17)+3•(-3)-2•(-8)=17-9+16=24.

Следовательно, V =1/6*24=4

36.Пдск. Координаты точки и координаты векторов. Преобразование координат при переходе к другой пдск.

Декартовые координаты вектора в ПДСК на плоскости и в пространстве.

Мы рассмотрим сразу общий случай координатного пространства.Координатная плоскость будет частным случаем, хотя можно все рассуждения повторить (практически дословно) и для плоскости.

   Пусть М – произвольная точка координатного пространства Охуz.

Определение. Вектор    называется радиус-вектором точки М.

Введем обозначения:

,  ,  .

Или, для произвольного вектора  :

             ,  ,  .

Определение. Проекции вектора   на координатные оси называются его декартовыми координатами.

Теорема. (О координатах точки и ее радиус-вектора.)

Координаты точки М в ПДСК в пространстве совпадают с декартовыми координатами её радиус-вектора.

   Доказательство.

    

                                          рис.9.

   По определению, координаты   точки М есть координатыточек   на координатных осях Ох, Оу, Оz соответственно, т.е.  ,  ,  . Так как точки М и   лежат в плоскости перпендикулярной оси Ох, то  . По аналогичной причине   и  . Отсюда и следуют доказываемые равенства:

,  ,  .

Теорема доказана.

   Заметим, что положение точки М в пространстве однозначно определяется ее координатами, т.е. существует взаимно однозначное соответствие между всеми точками пространства и упорядоченными тройками действительных чисел – их координатами. Вследствие этого, координатное пространство обозначают как декартов куб множества действительных чисел:  . (Соответственно координатную плоскость как декартов квадрат множества действительных чисел:  )

   Далее, очевидно, существует биекция и между всеми точкамипространства и их радиус-векторами, а значит и между  радиус-векторами точек пространства и  , т.е

их декартовыми координатами как упорядоченными тройками действительных чисел:

  .     (1)                   

   В силу этого взаимно однозначного соответствия принято отождествлять радиус-вектор   с упорядоченной тройкой его декартовых координат:

.

               .                               (2)

   Пусть   – произвольный вектор пространства и, отложив его от начала координат, получим  . Т.к. проекции вектора на оси не зависят от выбора точки его начала, то можно записать:

                ,                 (3)

т.е. существует взаимно однозначное соответствие между всемивекторами пространства и всеми упорядоченными тройками действительных чисел, их декартовыми координатами.

   Отсюда сразу же вытекает следующая теорема.

Теорема. (О равенстве векторов.)

 Два вектора равны тогда и только тогда, когда равны их декартовые координаты.

Определение. Запись вектора в виде (2) или (3) называется егокоординатной формой записи.

Теорема. (О действиях с векторами в координатной форме.)  При сложении векторов их декартовые координаты складываются, а при умножении вектора на число каждая декартовая координата вектора умножается на это число.

   Иначе, пусть  ,  ,  . Тогда: 1)  ;

            2)  .

   Доказательство. Сразу же следует из свойств проекции вектора на ось: 

.  .

Аналогично доказывается второе утверждение теоремы.

Теорема доказана.

Теорема. (О вычислении декартовых координат вектора.)

Для того, чтобы вычислить декартовые координаты вектора нужно изкоординат его конца вычесть координаты его начала.

   Иначе, пусть  и  ,   – координаты его начала и конца. Тогда

                                        (4)

   Доказательство. Пусть О(0; 0; 0) – начало координат. Тогда по правилу треугольника сложения векторов

                 

                                    рис.10.

  . Векторы   и   являются радиус-векторами точек А и В соответственно и их декартовые координаты совпадают с координатами этих точек:  ,  . Применяя теорему о действиях с векторами в координатной форме, получаем

              .

Теорема доказана.